石河子大学：《计量经济学》课程PPT教学课件（硕士生）第四章 经典单方程计量经济学模型（放宽基本假定的模型 Relaxing the Assumptions of the Classical Model）4.1 异方差性 Heteroscedasticity §4.2 序列相关性 Autocorrelation

第四章 经典单方程计量经济学模型： 放宽基本假定的模型 Reang the Assumptions of the Classical Model

第四章 经典单方程计量经济学模型： 放宽基本假定的模型 Relaxing the Assumptions of the Classical Model

基本假定违背主要包括： 一随机误差项序列存在异方差性 - 随机误差项序列存在序列相关性； -解释变量之间存在多重共线性； 解释变量是随机变量且与随机误差项相关的 随机解释变量问题； 模型设定有偏误； 解释变量的方差不随样本容量的增而收敛。 计量经济检验：对模型基本假定的检验 本章主要学习前4类

• 基本假定违背主要包括： – 随机误差项序列存在异方差性； – 随机误差项序列存在序列相关性； – 解释变量之间存在多重共线性； – 解释变量是随机变量且与随机误差项相关的 随机解释变量问题； – 模型设定有偏误； – 解释变量的方差不随样本容量的增而收敛。 • 计量经济检验：对模型基本假定的检验 • 本章主要学习前4类

54.1异方差性 Heteroscedasticity 一、 异方差的概念 二 异方差性的后果 三、异方差性的检验 四、 异方差的修正 五、 例题

§4.1 异方差性 Heteroscedasticity 一、异方差的概念 二、异方差性的后果 三、异方差性的检验 四、异方差的修正 五、例题

一、异方差的概念 1、异方差 Y=B。+BXi+B2X2+.+PXa+4 i=1,2,.,n ar(4)=o2 Homoscedasticity Var()=o 即对于不同的样本点， 随机误差项的方差不再 是常数，而互不相同，则认为出现了异方差性 (Heteroskedasticity)

Yi =  0 + 1 Xi i +  2 X2i ++  k Xki + i Var i i ( ) =  2 即对于不同的样本点，随机误差项的方差不再 是常数，而互不相同，则认为出现了异方差性 (Heteroskedasticity)。 1、异方差 i = 1,2,  , n 2 Var(i ) = Homoscedasticity 一、异方差的概念

2、异方差的类型 同方差：σ2=常数，与解释变量观测值X无关； 异方差：o2=X),与解释变量观测值X有关。 异方差一般可归结为三种类型： 单调递增型：σ随X的增大而增大 -单调递减型：σ2随X的增大而减小 -复杂型：σ2与X的变化呈复杂形式

2、异方差的类型 • 同方差：i 2 = 常数，与解释变量观测值Xi无关； 异方差：i 2 = f(Xi )，与解释变量观测值Xi有关。 • 异方差一般可归结为三种类型： – 单调递增型：i 2随X的增大而增大 – 单调递减型：i 2随X的增大而减小 – 复 杂 型： i 2与X的变化呈复杂形式

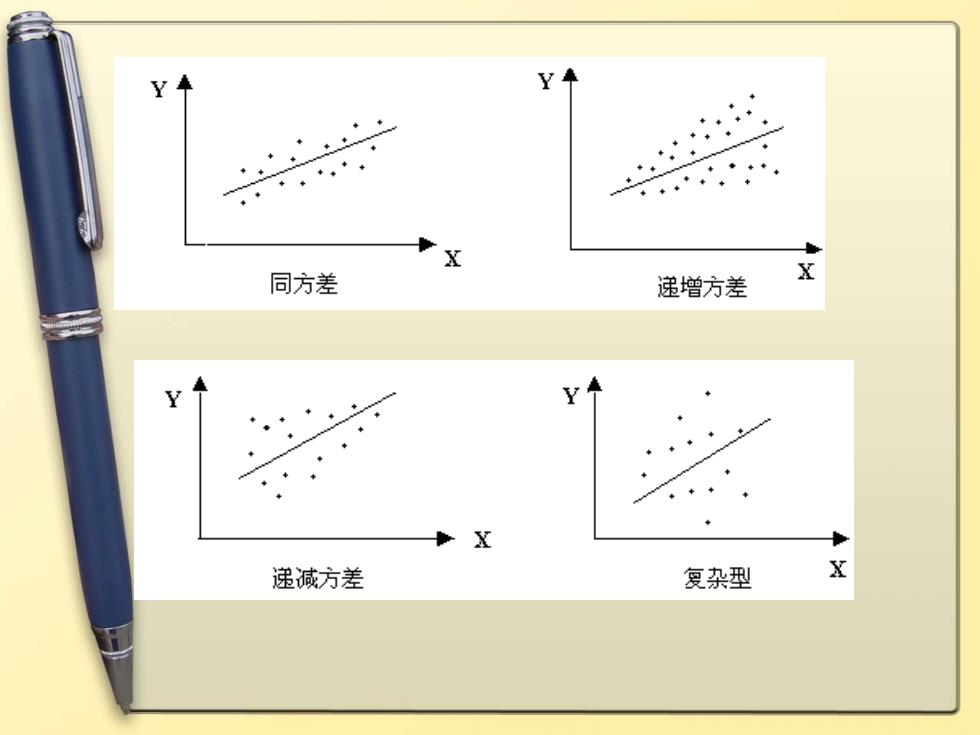
同方差 递增方差 递减方差 复杂型

3、实际经济问题中的异方差性 例4.1.1：截面资料下研究居民家庭的储蓄行为 YFβ0+β1Xt4 Y:第个家庭的储蓄额 X:第个家庭的可支配收入。 高收入家庭：储蓄的差异较大； 低收入家庭：储蓄则更有规律性，差异较小。 4的方差呈现单调递增型变化

3、实际经济问题中的异方差性 例4.1.1：截面资料下研究居民家庭的储蓄行为 Yi=0+1Xi+i Yi :第i个家庭的储蓄额 Xi :第i个家庭的可支配收入。 高收入家庭：储蓄的差异较大； 低收入家庭：储蓄则更有规律性，差异较小。 i的方差呈现单调递增型变化

例4.1.2：以绝对收入假设为理论假设、以截面 数据为样本建立居民消费函数： C=Bo+BY+u 将居民按照收入等距离分成组，取组平均数为 样本观测值。 般情况下，居民收入服从正态分布：中等 收入组人数多，两端收入组人数少。 而人数多 的组平均数的误差小，人数少的组平均数的误 差大。 样本观测值的观测误差随着解释变量观测值 的不同而不同，往往引起随机项的异方差性， 且皇U形

例4.1.2: 以绝对收入假设为理论假设、以截面 数据为样本建立居民消费函数： Ci= 0+1Yi+I 将居民按照收入等距离分成n组，取组平均数为 样本观测值。 • 一般情况下，居民收入服从正态分布：中等 收入组人数多，两端收入组人数少。而人数多 的组平均数的误差小，人数少的组平均数的误 差大。 样本观测值的观测误差随着解释变量观测值 的不同而不同，往往引起随机项的异方差性， 且呈U形

例4.1.3：以某一行业的企业为样本建立企业生 产函数模型 Y=A:BI K.B2L:B3eul 被解释变量：产出量Y,解释变量：资本K、劳 动L、技术A。 每个企业所处的外部环境对产出量的影响被 包含在随机误差项中。 对于不同的企业，它们对产出量的影响程度 不同，造成了随机误差项的异方差性。 随机误差项的方差并不随某一个解释变量观 测值的变化而呈规律性变化，呈现复杂型

例4.1.3: 以某一行业的企业为样本建立企业生 产函数模型 Yi=Ai 1Ki 2Li 3e I 被解释变量：产出量Y，解释变量：资本K、劳 动L、技术A。 • 每个企业所处的外部环境对产出量的影响被 包含在随机误差项中。 对于不同的企业，它们对产出量的影响程度 不同，造成了随机误差项的异方差性。 随机误差项的方差并不随某一个解释变量观 测值的变化而呈规律性变化，呈现复杂型

二、异方差性的后果 Consequences of Using OLS in the Presence of Heteroskedasticity

二、异方差性的后果 Consequences of Using OLS in the Presence of Heteroskedasticity