
第五章扩展的 计量经济学模型 §5.1变参数线性单方程计量经 济学模型 §5.2简单的非线性单方程计量 经济学模型 §5.3二元离散选择模型 §5.4固定影响平行数据模型
第五章 扩展的 计量经济学模型 §5.1变参数线性单方程计量经 济学模型 §5.2简单的非线性单方程计量 经济学模型 §5.3二元离散选择模型 §5.4固定影响平行数据模型

§5.1变参数线性计量经济学模型 ,一、确定性变参数模型 二、 随机变参数模型
§5.1 变参数线性计量经济学模型 ❖ 一、确定性变参数模型 ❖ 二、随机变参数模型

一、确定性变参数模型
一、确定性变参数模型

参数随某一个变量呈规律性变化 y,=C,+Bx,+4 a,=do+ap B=B+B卫: y,=0o+必1p,+B,+B卫p,x,+4 ·实际经济问题中的实例:具有经济意义的参数受 某一因素的影响
⒈参数随某一个变量呈规律性变化 y x t = t + t t + t t t t t p p = + = + 0 1 0 1 y p x p x t = 0 +1 t + 0 t + 1 t t + t • 实际经济问题中的实例:具有经济意义的参数受 某一因素的影响

模型的估计 p为确定性变量,与随机误差项不相关,可以用 OLS方法估计,得到参数估计量。 可以通过检验a1、B是否为0来检验变量p是否对a、 B有影响
❖ 模型的估计 p为确定性变量,与随机误差项不相关,可以用 OLS方法估计,得到参数估计量。 可以通过检验α1、β1是否为0来检验变量p是否对α、 β有影响
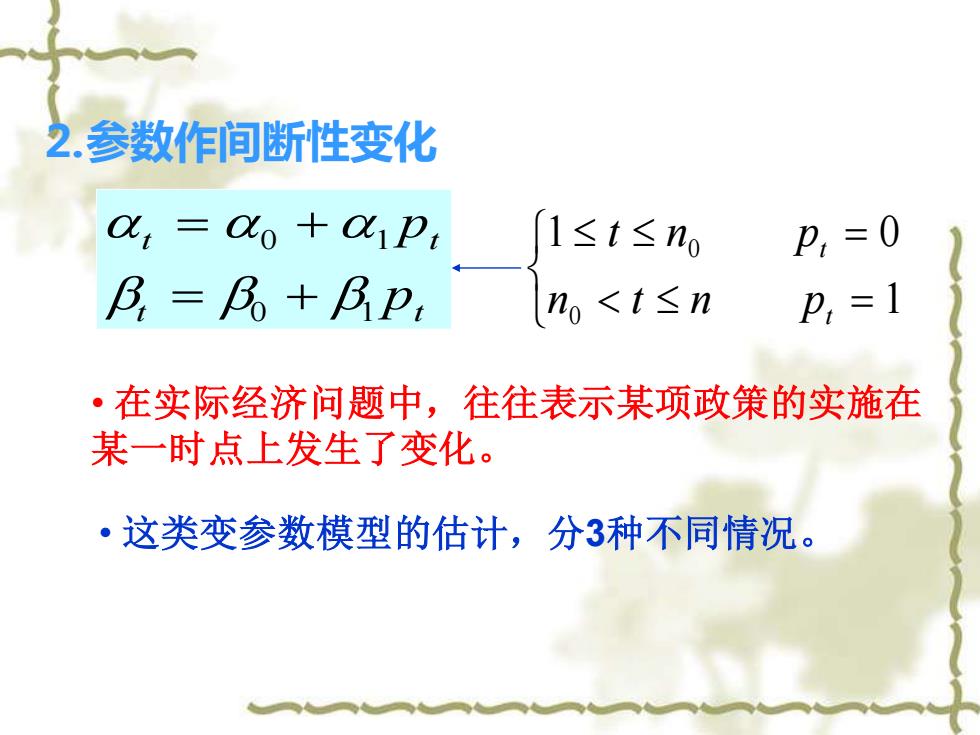
2.参数作间断性变化 a,=do+a p 1≤t≤no P,=0 B=B+BP no<t≤n 卫,=1 ·在实际经济问题中,往往表示某项政策的实施在 某一时点上发生了变化。 ·这类变参数模型的估计,分3种不同情况
⒉参数作间断性变化 t t t t p p = + = + 0 1 0 1 1 0 1 0 0 = = t n p n t n p t t • 在实际经济问题中,往往表示某项政策的实施在 某一时点上发生了变化。 • 这类变参数模型的估计,分3种不同情况

o已知,则可以分段建立模型,分段估计模型; 也可以引入虚变量,建立一个统一的模型。 ·n未知,但Var(4r)=Var(h2,) 一般可以选择不同的no,进行试估计,然后从多 次试估计中选择最优者。选择的标准是使得两段方 程的残差平方和之和最小。 n未知,且Var(hz)≠Var(ht) 将no看作待估参数,用最大或然法进行估计
❖ n0已知,则可以分段建立模型,分段估计模型; 也可以引入虚变量,建立一个统一的模型。 • n0未知,但 Var Var t t ( ) ( ) 1 = 2 一般可以选择不同的n0 ,进行试估计,然后从多 次试估计中选择最优者。选择的标准是使得两段方 程的残差平方和之和最小。 • n0未知,且 Var Var t t ( ) ( ) 1 2 将n0看作待估参数,用最大或然法进行估计

二、随机变参数模型
二、随机变参数模型

参数在一常数附近随机变化 c,=a+e,f=B+7. 。将原模型转换为具有异方差性的模型,而且已经推 导出随机误差项的方差与解释变量之间的函数关系。 ÷可以采用经典线性计量经济学模型中介绍的估计方 法,例如加权最小二乘法等方法很方便地估计参数。 ,一种普遍的形式是1968年提出的的变参数 Hildreth-Houck模型
⒈ 参数在一常数附近随机变化 ❖ 将原模型转换为具有异方差性的模型,而且已经推 导出随机误差项的方差与解释变量之间的函数关系。 ❖ 可以采用经典线性计量经济学模型中介绍的估计方 法,例如加权最小二乘法等方法很方便地估计参数。 ❖ 一种普遍的形式是1968年提出的的变参数 Hildreth-Houck模型 。 t = + t t = +t

2.参数随某一变量作规律性变化,同时受随 机因素影响 0,=0+8卫,+8, B=B+δp,+7, ÷将原模型转换为具有异方差性的多元线性模型。 ·可以采用经典线性计量经济学模型中介绍的估计方 法,例如加权最小二乘法等方法很方便地估计参数
⒉ 参数随某一变量作规律性变化,同时受随 机因素影响 ❖ 将原模型转换为具有异方差性的多元线性模型。 ❖ 可以采用经典线性计量经济学模型中介绍的估计方 法,例如加权最小二乘法等方法很方便地估计参数。 t t t = + p + t = + pt + t