
§6.2随机时间 序列分析模型
1 §6.2 随机时间 序列分析模型

教学内容 ·一、时间序列模型的基本概念及其适用性 。」 二、随机时间序列模型的平稳性条件 。 三、随机时间序列模型的识别 四、随机时间序列模型的估计 ·五、随机时间序列模型的检验
2 教学内容 • 一、时间序列模型的基本概念及其适用性 • 二、随机时间序列模型的平稳性条件 • 三、随机时间序列模型的识别 • 四、随机时间序列模型的估计 • 五、随机时间序列模型的检验

。1 经典计量经济学模型 。 时间序列模型 ·确定性时间序列模型 随机性时间序列模型
3 • 经典计量经济学模型 • 时间序列模型 • 确定性时间序列模型 • 随机性时间序列模型
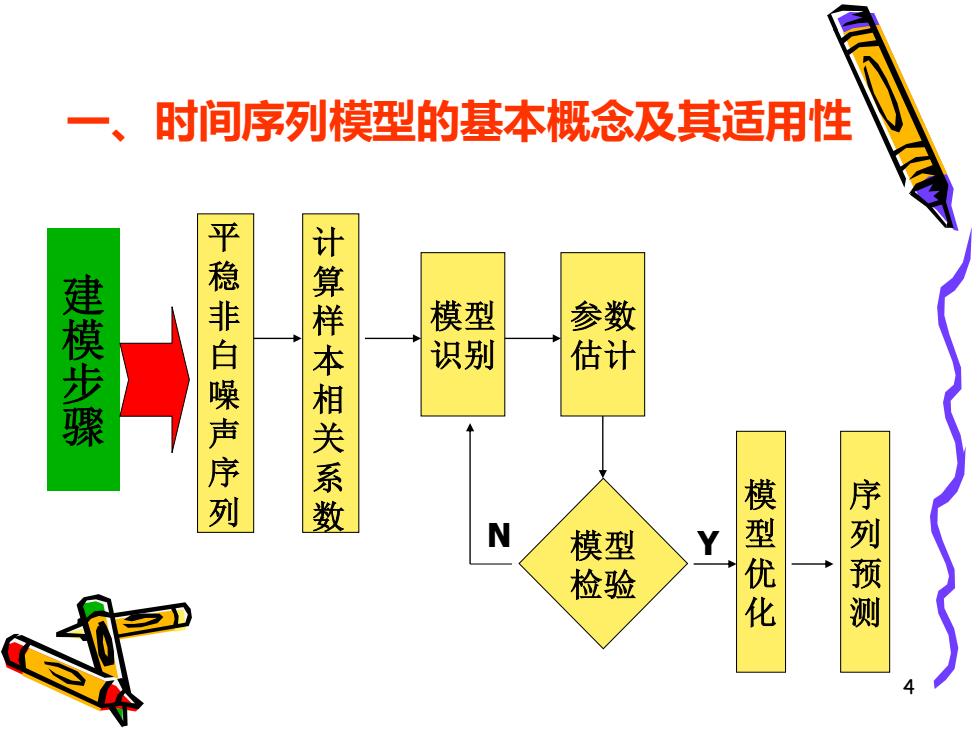
一、 时间序列模型的基本概念及其适用性 建模步骤 稳非白噪声序列 算样本相关系数 模型 参数 识别 估计 N 模型 Y 检验 模型优化 序列预测
4 一、时间序列模型的基本概念及其适用性 建 模 步 骤 平 稳 非 白 噪 声 序 列 计 算 样 本 相 关 系 数 模型 识别 参数 估计 模型 检验 模 型 优 化 序 列 预 测 N Y

7 1、时间序列模型的基本概念 随机时间序列模型(time series modeling)是指仅用它的过去值及随机扰动 项所建立起来的模型,其一般形式为 X=F(Xt-1,Xt-2.) 建立具体的时间序列模型,需解决如下三个 问题: (1)模型的具体形式 (2)时序变量的滞后期 )随机扰动项的结构
5 1、时间序列模型的基本概念 随 机 时 间 序 列 模 型 ( time series modeling)是指仅用它的过去值及随机扰动 项所建立起来的模型,其一般形式为 Xt=F(Xt-1 , Xt-2 , ., t ) 建立具体的时间序列模型,需解决如下三个 问题: (1)模型的具体形式 (2)时序变量的滞后期 (3)随机扰动项的结构

例如,取线性方程、一期滞后以及白噪声 随机扰动项(+=+), 模型将是一个1阶自回归过程AR(1): X+=0X+-1t8+ 这里,+特指一白噪声
6 例如,取线性方程、一期滞后以及白噪声 随机扰动项( t =t), 模型将是一个1阶自回归过程AR(1): Xt=Xt-1+ t 这里, t特指一白噪声

随机性时间序列模型的特点 ·建摸过程是一个反复实验的过程 借助自相关函数值和偏自相关函数值确定模型的类型 利用时间序列中的自相关关系进行分析和建摸:时间序列的自相关关 系是指时间序列在不同时期观测值之间的相关关系 ·许多因素产生的影响不是瞬间的,而是持续几个时期或更长时间,因 此时间序列在不同时期的值往往存在较强的相关关系 ·用自相关函数和偏自相关函数衡量时间序列中的自相关关系 借助诊断性检验判断模型的实用性
7 随机性时间序列模型的特点 • 建摸过程是一个反复实验的过程 • 借助自相关函数值和偏自相关函数值确定模型的类型 • 利用时间序列中的自相关关系进行分析和建摸:时间序列的自相关关 系是指时间序列在不同时期观测值之间的相关关系 • 许多因素产生的影响不是瞬间的,而是持续几个时期或更长时间,因 此时间序列在不同时期的值往往存在较强的相关关系 • 用自相关函数和偏自相关函数衡量时间序列中的自相关关系 • 借助诊断性检验判断模型的实用性
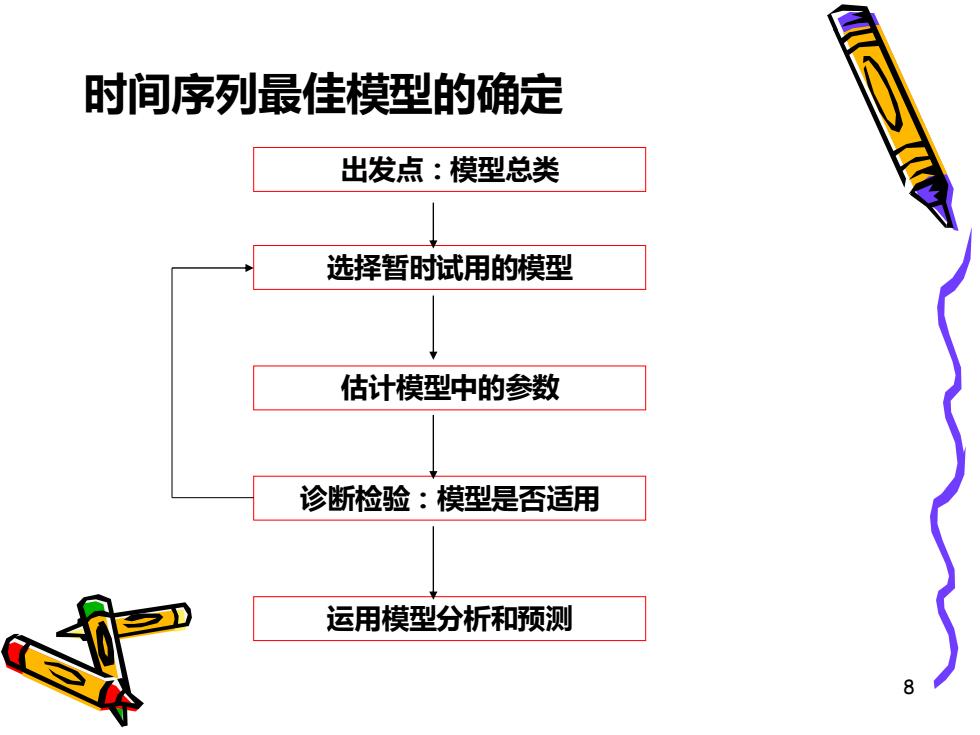
时间序列最佳模型的确定 出发点:模型总类 选择暂时试用的模型 估计模型中的参数 诊断检验:模型是否适用 运用模型分析和预测
8 时间序列最佳模型的确定 出发点:模型总类 选择暂时试用的模型 估计模型中的参数 诊断检验:模型是否适用 运用模型分析和预测

模型分类 ·总类模型 ·移动平均模型MA(q)(Moving Average) 自回归模型AR(p)(Autoregression) ·混合自回归移动平均模型ARMA(P,q) 。 差分自回归-移动平均模型ARIMA(P,d,q)
9 模型分类 • 总类模型 • 移动平均模型 MA(q) (Moving Average) • 自回归模型 AR(p) (Autoregression) • 混合自回归移动平均模型 ARMA (p,q) • 差分自回归-移动平均模型 ARIMA (p,d,q)

总类模型 y:=L+8t+PE-1+P2Ei-2+. =u+∑p,e,y Po =1 p,是莫型中的参数 10
10 总类模型 1 1 2 2 . t t t t j t j j y − − − = + + + + = + 0 1 , j = 是模型中的参数