
§6.4联立方程计量经济学模型的系统 估计方法 the Systems Estimation Methods 一、】 联立方程模型随机误差项方差一协 方差矩阵 二、三阶段最小二乘法简介 三、完全信息最大似然法简介
§6.4联立方程计量经济学模型的系统 估计方法 the Systems Estimation Methods 一、联立方程模型随机误差项方差—协 方差矩阵 二、三阶段最小二乘法简介 三、完全信息最大似然法简介

一、联立方程模型随机误差项方 差一协方差矩阵
一、联立方程模型随机误差项方 差—协方差矩阵

1.随机误差项的同期相关性 ·随机误差项的相关性不仅存在于每个结构方程 不同样本点之间,而且存在于不同结构方程之 间。 。 对于不同结构方程的随机误差项之间,不同时 期互不相关,只有同期的随机误差项之间才相 关,称为具有同期相关性
⒈随机误差项的同期相关性 • 随机误差项的相关性不仅存在于每个结构方程 不同样本点之间,而且存在于不同结构方程之 间。 • 对于不同结构方程的随机误差项之间,不同时 期互不相关,只有同期的随机误差项之间才相 关,称为具有同期相关性
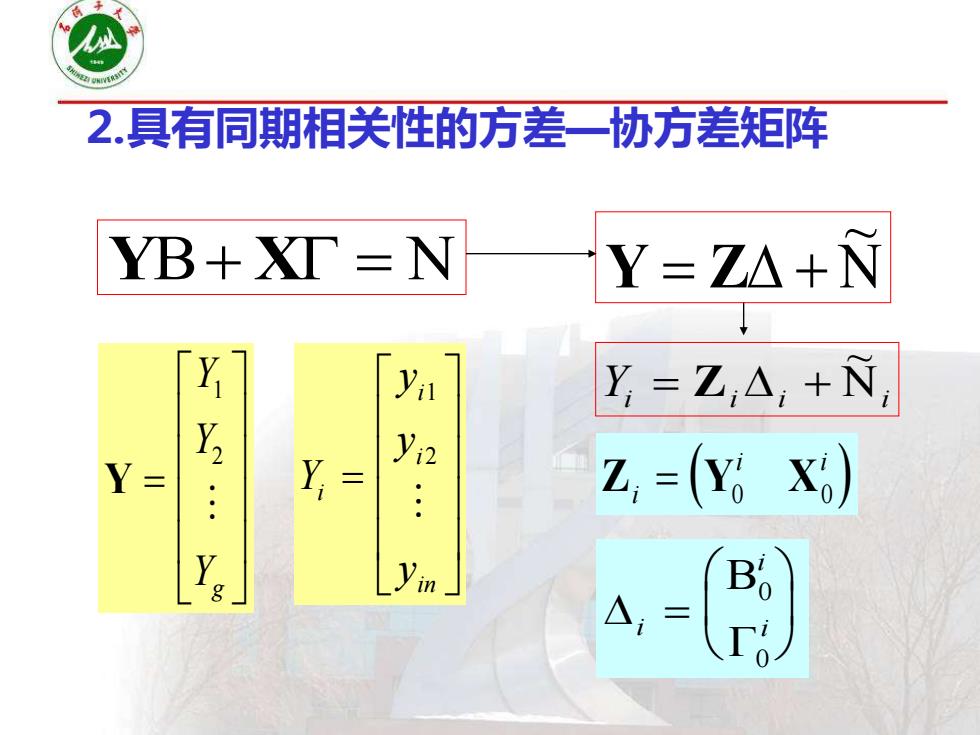
2.具有同期相关性的方差一协方差矩阵 YB+XT=N Y=ZA+N ya Y,=Z,△,+N, Y= 三 Z.=(Yo xo) yin 0
⒉具有同期相关性的方差—协方差矩阵 Y+ X = Y = Z + ~ Y = Y Y Yg 1 2 Y y y y i i i in = 1 2 Yi = Zi i + i ~ Z (Y X ) i i i = 0 0 i i = i 0 0

假设: ·对于一个结构方程的随机误差项,在不同样本 点之间,具有同方差性和序列不相关性。即 Cov(N,)=o2I ·对于不同结构方程的随机误差项之间,具有且仅 具有同期相关性。即 Cov(NN)=o,I
假设: • 对于一个结构方程的随机误差项,在不同样本 点之间,具有同方差性和序列不相关性。即 Cov i ii ( ~ ) = 2 I • 对于不同结构方程的随机误差项之间,具有且仅 具有同期相关性。即 Cov i j ij ( ~ , ~ ) = I

于是,联立方程模型系统随机误差项方差一协方 差矩阵为: GiI OpI 01g1 Cov(N) 02I 0a1 02g 0g1I( g2I 88 =∑⑧I =2
于是,联立方程模型系统随机误差项方差—协方 差矩阵为: Cov g g g g gg ( ~ ) = 11 2 12 1 21 22 2 2 1 2 2 I I I I I I I I I = = I

二、三阶段最小二乘法简介 (3SLS,Three Stages Least Squares)
二、三阶段最小二乘法简介 (3SLS,Three Stages Least Squares)

1概念 ·3SLS是由Zellner和Theil-于1962年提出的同时 估计联立方程模型全部结构方程的系统估计方 法。 。 其基本思路是3SLS=2SLS+GLS 即首先用2SLS估计模型系统中每一个结构方 程,然后再用GLS估计模型系统
⒈概念 • 3SLS是由Zellner和Theil于1962年提出的同时 估计联立方程模型全部结构方程的系统估计方 法。 • 其基本思路是 3SLS=2SLS+GLS 即首先用2SLS估计模型系统中每一个结构方 程,然后再用GLS估计模型系统

2.三阶段最小二乘法的步骤 (1)用2SLS估计结构方程 Y=Z,△,+N 得到方程随机误差项的估计值
⒉三阶段最小二乘法的步骤 ⑴ 用2SLS估计结构方程 Yi = Zi i + i ~ 得到方程随机误差项的估计值

Z,=(YX)一Y0=XTΠ+E OLS =X(XX)X 估计 之,=(X) OLS估计 △,=(22,)2X =立,△,e=-
Z (Y X ) i i i = 0 0 Y0 X 0 0 i i i = + Y0 X 0 X(X X) X Y 1 0 i i i = = − ( ) Zi Y X i i = 0 0 ( ) i = i i i Yi − Z Z Z 1 Yi = Zi i e y y il = il − il OLS 估计 OLS估计