石河子大学：《计量经济学》课程PPT教学课件（本科）第五章 序列相关性

石闭手大学 SHIHEZI UNIVERSITY 目录 序列相关性概念 ■二、 实际经济问题中的序列相关性 三、 序列相关性的后果 ■四、序列相关性的检验 ■五、 具有序列相关性模型的估计 ■六、案例 2024/9/22 石河子大学经管学院一一唐勇

2024/9/22 石河子大学经管学院－－唐勇 2 ◼一、序列相关性概念 ◼二、实际经济问题中的序列相关性 ◼三、序列相关性的后果 ◼四、序列相关性的检验 ◼五、具有序列相关性模型的估计 ◼六、案例 目录

名两多大学 序列相关性概念 SHIHEZI UNIVERSITY ■对于模型 Vi=Bo+B1Xi+B2X2i+.+BkXki+i i=1,2,n 随机项互不相关的基本假设表现为 Cov(4,=0≠i=1,2,n 如果对于不同的样本点，随机误差项之间不再是 不相关的，而是存在某种相关性，则认为出现了 序列相关性。 2024/9/22 石河子大学经管学院一一唐勇

2024/9/22 石河子大学经管学院－－唐勇 3 如果对于不同的样本点，随机误差项之间不再是 不相关的，而是存在某种相关性，则认为出现了 序列相关性。 ◼对于模型 Yi= 0+ 1X1i+ 2X2i+.+ kXki+i i=1,2, .,n 随机项互不相关的基本假设表现为 Cov(i , j )=0 ij, i,j=1,2, .,n 一、序列相关性概念

石闭手大学 、序列相关性概念 SHIHEZI UNIVERSITY 在其他假设仍成立的条件下，序列相关即意味着 E(4,4）≠0 或 03 E(44n） COv(μ)=E(μ)= E(μn41) 03 =σ22≠21 2024/9/22 石河子大学经管学院一一唐勇

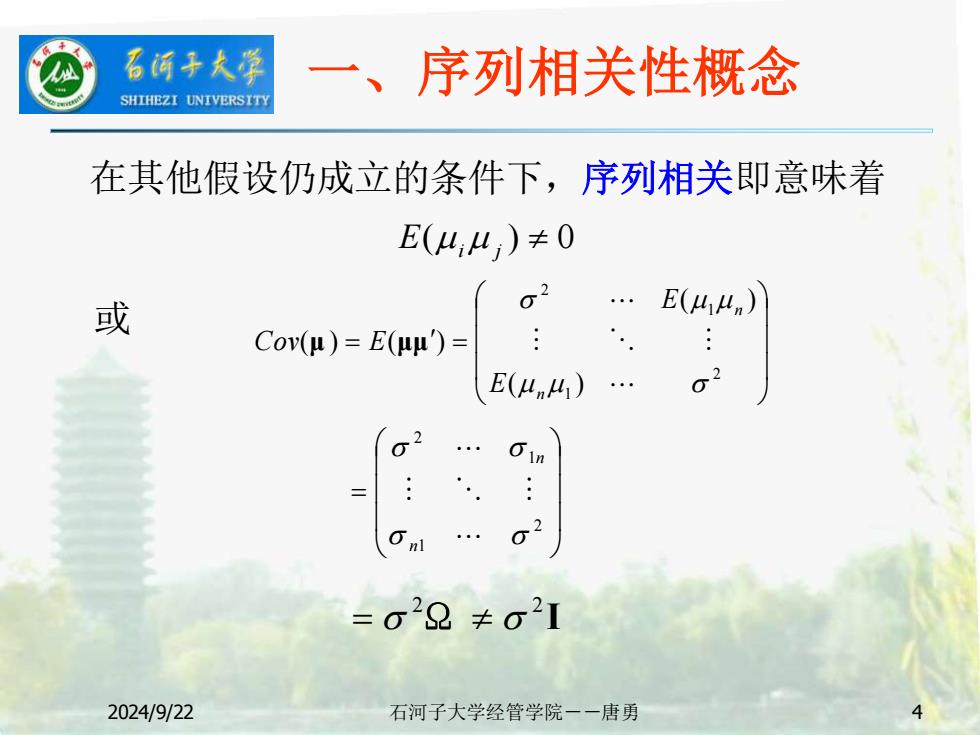
2024/9/22 石河子大学经管学院－－唐勇 4 在其他假设仍成立的条件下，序列相关即意味着 E( i  j )  0           =  = 2 1 1 2 ( ) ( ) ( ) ( )            n n E E Cov μ E μμ           = 2 1 1 2          n n Ω I 2 2 =    或 一、序列相关性概念

名两多大学 、 序列相关性概念 SHIHEZI UNIVERSITY ■如果仅存在 E(h+1)≠0 ，则称一阶自相关 ■自相关往往可写成如下形式： ufpui1+8i -1<p<1 其中：ε是满足以下标准的OLS假定的随机干 扰项： E(e,)=0, var(8,)=o2, C0NMe,8-)=0 5≠0 ■由于序列相关性经常出现在以时间序列为样本 的模型中，因此，本章将用下标代表。 2024/9/22 石河子大学经管学院一一唐勇

2024/9/22 石河子大学经管学院－－唐勇 5 其中：i是满足以下标准的OLS假定的随机干 扰项： ◼如果仅存在 E(i i+1)0 ， 则称一阶自相关 ◼自相关往往可写成如下形式： i=i-1+i -1<<1 ( ) = 0 E i  , 2 var( i ) =  , cov( , ) = 0 i i−s   s  0 ◼由于序列相关性经常出现在以时间序列为样本 的模型中，因此，本章将用下标t代表i。 一、序列相关性概念

名闭手大学 二、序列相关性产生的原因 SHIHEZI UNIVERSITY 1、 经济惯性 ■2、设定偏误 >应含而未含变量的情形 >不正确的函数形式 ■3、蛛网现象(Cobweb phenomenon) ■4、滞后效应 ■5、数据的“编造” ■自相关也可能出现在横截面数据中，但更一般 出现在时间序列数据中。 2024/9/22 石河子大学经管学院一一唐勇

2024/9/22 石河子大学经管学院－－唐勇 6 二、序列相关性产生的原因 ◼ 1、经济惯性 ◼ 2、设定偏误 ➢应含而未含变量的情形 ➢不正确的函数形式 ◼ 3、蛛网现象(Cobweb phenomenon) ◼ 4、滞后效应 ◼ 5、数据的“编造” ◼ 自相关也可能出现在横截面数据中，但更一般 出现在时间序列数据中

名闻手大学 三、序列相关性的后果 SHIHEZI UNIVERSITY ■计量经济学模型一旦出现序列相关性，如 果仍采用OLS法估计模型参数，会产生下列 不良后果： 1、参数估计量非有效 2、变量的显著性检验失去意义 3、参数估计量的可靠性降低 4、模型的预测失效 2024/9/22 石河子大学经管学院一一唐勇

2024/9/22 石河子大学经管学院－－唐勇 7 ◼计量经济学模型一旦出现序列相关性，如 果仍采用OLS法估计模型参数，会产生下列 不良后果： 1、参数估计量非有效 三、序列相关性的后果 2、变量的显著性检验失去意义 3、参数估计量的可靠性降低 4、模型的预测失效

石闭手大学 SHIHEZI UNIVERSITY 1、线性性，即估计量。、乃，是，的线性组合。 证：A=出-2心-刀 ∑T∑ ∑ ∑对一∑x∑ 令，因2-2x-=0,故有 A-22=2以 A=F-r=∑x-∑r=∑分a,g=∑ 2024/9/22 石河子大学经管学院一一唐勇

2024/9/22 石河子大学经管学院－－唐勇 8

名怀手大学 SHIHEZI UNIVERSITY 2、无偏性，即估计量。、B,的均值（期望）等于总体回归 参数真值B与B 证：A=∑kg=∑k(B+BX,+4,)=A∑k+B∑kX,+∑4 易知 ∑kX,=1 故B=B,+∑k山 E(B)=E(B+∑k4,)=B+∑k,E(4)=B 同样地，容易得出 E(B)=E(B+∑w,4,)=E(B)+∑w,E(4,)=B。 2024/9/22 石河子大学经管学院一一唐勇

2024/9/22 石河子大学经管学院－－唐勇 9 2、无偏性，即估计量 0 ˆ  、 1 ˆ  的均值（期望）等于总体回归 参数真值0与1 证： =  i i =  i + i + i =  i +  i i + i i  ˆ 1 k Y k ( 0 1 X  )  0 k 1 k X k  易知 0 2  = =   i i i x x k  = 1 i Xi k 故 = +  i i  ˆ 1 1 k  1 = 1 + = 1 + = 1 ) ( ) ( ) ˆ E( E  ki  i  ki E  i  同样地，容易得出 0 = 0 + = 0 + = 0 ) ( ) ( ) ( ) ˆ E( E  wi  i E  wi E  i 

石闭手大学 SHIHEZI UNIVERSITY 3、非有效性 月=R ∑弘 ∑x va i)any 分E0+2空4) ∑x ∑2 2024/9/22 石河子大学经管学院一一唐勇 10

2024/9/22 石河子大学经管学院－－唐勇 10  = +  1 1 2 ˆ t t t x x u   1 (1) ) ˆ var( AR 2 2 2 1 1 ) ( ) ˆ (  = − =  t t t x x u E   E ) ( 2 ) 1 ( 2 2 2 2     + t s t t t s t s t E x u x x u u x t s t t s t s u t u x x x x  −    +    2 2 2 2 2 3、非有效性

名两子大学 四、序列相关性的检验 SHIHEZI UNIVERSITY ■基本思路： ■序列相关性检验方法有多种，但基本思路相同： 首先，采用OLS法估计模型，以求得随机误差项的 “近似估计量”，用e,表示： e,=Y,-()os 然后，通过分析这些“近似估计量”之间的相关性 以判断随机误差项是否具有序列相关性。 2024/9/22 石河子大学经管学院一一唐勇 11

2024/9/22 石河子大学经管学院－－唐勇 11 四、序列相关性的检验 ◼序列相关性检验方法有多种，但基本思路相同： 首先，采用 OLS 法估计模型，以求得随机误差项的 “近似估计量”，用~ei表示： i Yi Yi l s e 0 ) ˆ ( ~ = − ◼基本思路: 然后，通过分析这些“近似估计量”之间的相关性， 以判断随机误差项是否具有序列相关性