
第四章 经典单方程计量经济学模型:放宽基 本假定的模型 Relaxing the Assumptions of the Classical Model
第四章 经典单方程计量经济学模型:放宽基 本假定的模型 Relaxing the Assumptions of the Classical Model

本章说明 ·基本假定违背主要包括: 一随机误差项序列存在异方差性; 一随机误差项序列存在序列相关性; -解释变量之间存在多重共线性; 、 解释变量是随机变量且与随机误差项相关的随机解 释变量问题; -模型设定有偏误; 一解释变量的方差不随样本容量的增而收敛。 ·计量经济检验:对模型基本假定的检验 ·本章主要讨论前4类
本章说明 • 基本假定违背主要 包括: – 随机误差项序列存在异方差性; – 随机误差项序列存在序列相关性; – 解释变量之间存在多重共线性; – 解释变量是随机变量且与随机误差项相关的随机解 释变量问题; – 模型设定有偏误; – 解释变量的方差不随样本容量的增而收敛。 • 计量经济检验:对模型基本假定的检验 • 本章主要讨论前4类

为什么不讨论正态性假设? William H.Greene(2003),Econometric Analysis In most cases,the zero mean assumption is not restrictive. In view ofour description of the source of the disturbances,the conditions of the central limit theorem will generally apply,at least approximately,and the normality assumption will be reasonable in most settings.Except in those cases in which some alternative distribution is assumed,the normality assumption is probably quite reasonable
为什么不讨论正态性假设? William H. Greene(2003), Econometric Analysis • In most cases, the zero mean assumption is not restrictive. • In view of our description of the source of the disturbances, the conditions of the central limit theorem will generally apply, at least approximately, and the normality assumption will be reasonable in most settings. Except in those cases in which some alternative distribution is assumed, the normality assumption is probably quite reasonable

实际上:正态性假设的违背 当存在模型关系误差时,如果解释变量是随机的, 随机误差项的正态性将得不到保证。 当模型遗漏了显著的变量,如果遗漏的变量是非正 态的随机变量,随机误差项将不具有正态性。 - 如果待估计的模型是原模型经过函数变换得到的, 随机误差项将不再服从正态分布。 当模型存在被解释变量的观测误差,如果观测误差 相对于随机误差项的标准差特别大、样本长度又特 别小,随机误差项的正态性假设会导致显著性水平 产生一定程度的扭曲。 当模型存在解释变量观测误差时,一般情况下,随 机误差项的正态性假设都是不能成立的;只有在回 归函数是线性的,且观测误差分布是正态的特殊情 形下,随机误差项的正态性才成立
实际上:正态性假设的违背 – 当存在模型关系误差时,如果解释变量是随机的, 随机误差项的正态性将得不到保证。 – 当模型遗漏了显著的变量,如果遗漏的变量是非正 态的随机变量,随机误差项将不具有正态性。 – 如果待估计的模型是原模型经过函数变换得到的, 随机误差项将不再服从正态分布。 – 当模型存在被解释变量的观测误差,如果观测误差 相对于随机误差项的标准差特别大、样本长度又特 别小,随机误差项的正态性假设会导致显著性水平 产生一定程度的扭曲。 – 当模型存在解释变量观测误差时,一般情况下,随 机误差项的正态性假设都是不能成立的;只有在回 归函数是线性的,且观测误差分布是正态的特殊情 形下,随机误差项的正态性才成立

§4.1异方差性 Heteroscedasticity 三 异方差的概念 异方差性的后果 三 异方差性的检验 四、 异方差的修正 五、 例题
§4.1 异方差性 Heteroscedasticity 一、异方差的概念 二、异方差性的后果 三、异方差性的检验 四、异方差的修正 五、例题

一、异方差的概念
一、异方差的概念

1、异方差 Y=B+BXi+P2X2:+.+PX后+4 i=1,2,.,n Var(u )=o2 Homoscedasticity Var(u)=o 即对于不同的样本点,随机误差项的方差不再 是常数,而互不相同,则认为出现了异方差性 (Heteroskedasticity)o
Yi = 0 + 1 Xi i + 2 X2i ++ k Xki + i Var i i ( ) = 2 即对于不同的样本点,随机误差项的方差不再 是常数,而互不相同,则认为出现了异方差性 (Heteroskedasticity)。 1、异方差 i = 1,2, , n 2 Var(i ) = Homoscedasticity

2、异方差的类型 ·同方差:o2=常数,与解释变量观测值X无关; 异方差:σ2=fX),与解释变量观测值X有关。 。异方差一般可归结为三种类型: -单调递增型:σ2随X的增大而增大 -单调递减型:σ随X的增大而减小 -复杂型:σ2与X的变化呈复杂形式
2、异方差的类型 • 同方差:i 2 = 常数,与解释变量观测值Xi无关; 异方差:i 2 = f(Xi ),与解释变量观测值Xi有关。 • 异方差一般可归结为三种类型: – 单调递增型:i 2随X的增大而增大 – 单调递减型:i 2随X的增大而减小 – 复 杂 型: i 2与X的变化呈复杂形式
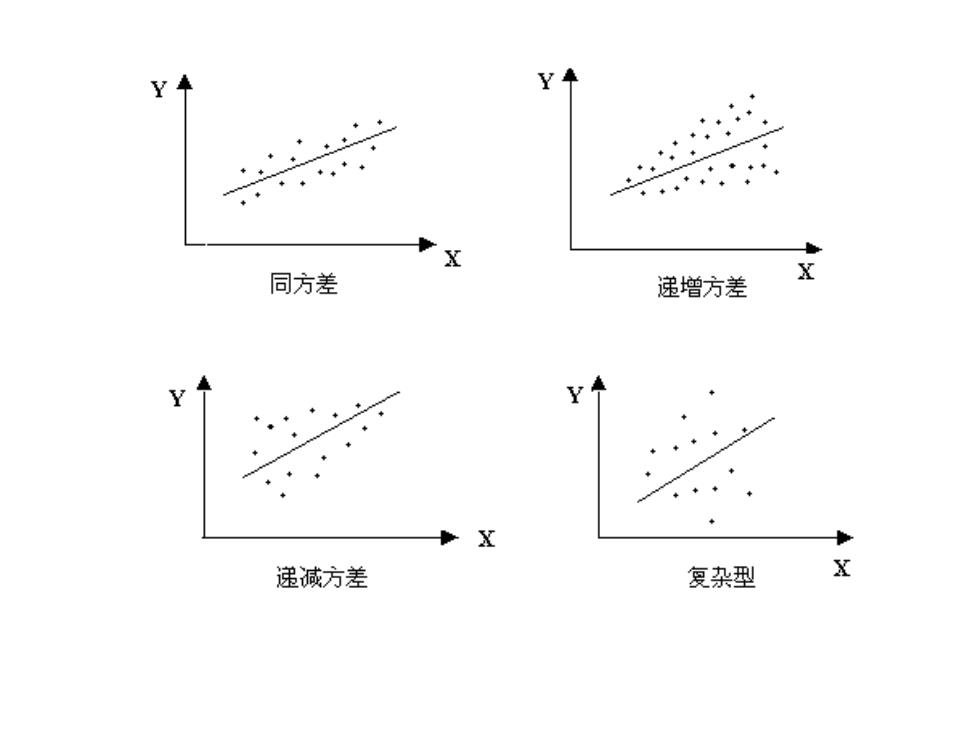
◆ 同方差 递增方差 递减方差 复杂型 X

3、实际经济问题中的异方差性 例4.1.1:截面资料下研究居民家庭的储蓄行为 Y=Bo+B Xi+u Y:第个家庭的储蓄额X:第个家庭的可支配收入。 高收入家庭:储蓄的差异较大; 低收入家庭:储蓄则更有规律性,差异较小。 4的方差呈现单调递增型变化
3、实际经济问题中的异方差性 例4.1.1:截面资料下研究居民家庭的储蓄行为 Yi=0+1Xi+i Yi :第i个家庭的储蓄额 Xi :第i个家庭的可支配收入。 高收入家庭:储蓄的差异较大; 低收入家庭:储蓄则更有规律性,差异较小。 i的方差呈现单调递增型变化