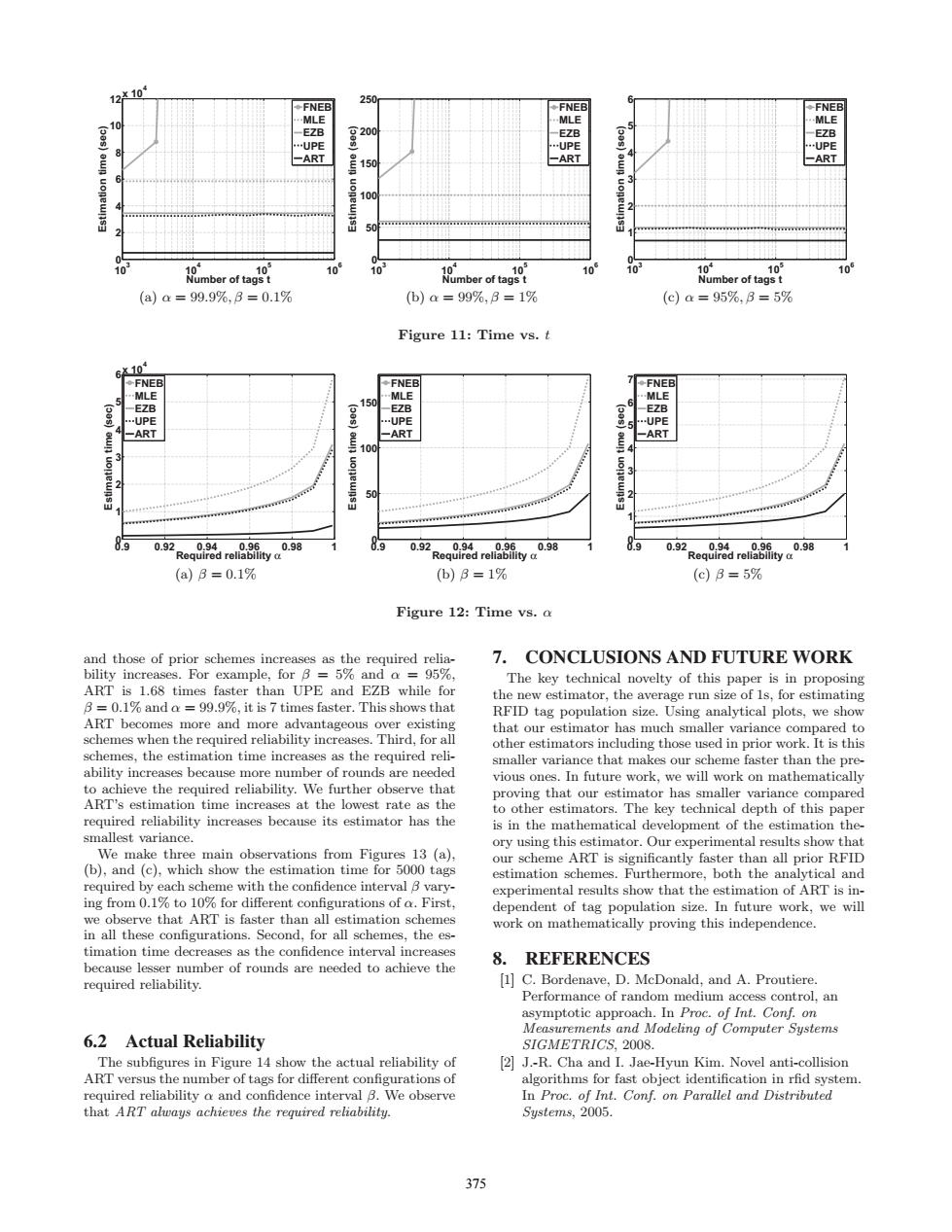
10 250 ◆FNEB ◆FNEB ◆FNEE MLE 10 MLE MLE -EZB 8200 -EZB B ..UPE .UPE .UPE -ART 150 -ART -ART 100 10 10 0 10 103 10 10 (a)a=99.9%,B=0.1% b)a=99%,B=1% (c)a=95%,B=5% Figure 11:Time vs.t 610 ◆FNEB ◆FNEB ◆FNEB MLE MLE MLE EZB 150 EZB EZB ..UPE ..UPE UP日 -ART -ART -ART 号100 Req89arel88盟tya9 0.92 0.94 0.98 0.92 094.096 0.98 0.98 Required reliability a 092Rea89drei888bya (a)B=0.1% (b)B=1% (c)B=5% Figure 12:Time vs.a and those of prior schemes increases as the required relia- 7.CONCLUSIONS AND FUTURE WORK bility increases.For example,for B =5%and a =95%, The key technical novelty of this paper is in proposing ART is 1.68 times faster than UPE and EZB while for the new estimator,the average run size of ls,for estimating B=0.1%and a =99.9%,it is 7 times faster.This shows that RFID tag population size.Using analytical plots,we show ART becomes more and more advantageous over existing that our estimator has much smaller variance compared to schemes when the required reliability increases.Third,for all other estimators including those used in prior work.It is this schemes,the estimation time increases as the required reli- smaller variance that makes our scheme faster than the pre- ability increases because more number of rounds are needed vious ones.In future work,we will work on mathematically to achieve the required reliability.We further observe that proving that our estimator has smaller variance compared ART's estimation time increases at the lowest rate as the to other estimators.The key technical depth of this paper required reliability increases because its estimator has the is in the mathematical development of the estimation the- smallest variance. ory using this estimator.Our experimental results show that We make three main observations from Figures 13(a), our scheme ART is significantly faster than all prior RFID (b),and(c),which show the estimation time for 5000 tags estimation schemes.Furthermore,both the analytical and required by each scheme with the confidence interval B vary- experimental results show that the estimation of ART is in- ing from 0.1%to 10%for different configurations of a.First, dependent of tag population size.In future work,we will we observe that ART is faster than all estimation schemes work on mathematically proving this independence. in all these configurations.Second,for all schemes,the es- timation time decreases as the confidence interval increases 8.REFERENCES because lesser number of rounds are needed to achieve the required reliability. [1]C.Bordenave,D.McDonald,and A.Proutiere. Performance of random medium access control,an asymptotic approach.In Proc.of Int.Conf.on Measurements and Modeling of Computer Systems 6.2 Actual Reliability SIGMETRICS,2008. The subfigures in Figure 14 show the actual reliability of [2]J.-R.Cha and I.Jae-Hyun Kim.Novel anti-collision ART versus the number of tags for different configurations of algorithms for fast object identification in rfid system. required reliability a and confidence interval B.We observe In Proc.of Int.Conf.on Parallel and Distributed that ART always achieves the required reliability. Systems,2005 375103 104 105 106 0 2 4 6 8 10 12x 104 Number of tags t Estimation time (sec) FNEB MLE EZB UPE ART (a) α = 99.9%, β = 0.1% 103 104 105 106 0 50 100 150 200 250 Number of tags t Estimation time (sec) FNEB MLE EZB UPE ART (b) α = 99%, β = 1% 103 104 105 106 0 1 2 3 4 5 6 Number of tags t Estimation time (sec) FNEB MLE EZB UPE ART (c) α = 95%, β = 5% Figure 11: Time vs. t 0.9 0.92 0.94 0.96 0.98 1 0 1 2 3 4 5 6x 104 Required reliability α Estimation time (sec) FNEB MLE EZB UPE ART (a) β = 0.1% 0.9 0.92 0.94 0.96 0.98 1 0 50 100 150 Required reliability α Estimation time (sec) FNEB MLE EZB UPE ART (b) β = 1% 0.9 0.92 0.94 0.96 0.98 1 0 1 2 3 4 5 6 7 Required reliability α Estimation time (sec) FNEB MLE EZB UPE ART (c) β = 5% Figure 12: Time vs. α and those of prior schemes increases as the required relia￾bility increases. For example, for β = 5% and α = 95%, ART is 1.68 times faster than UPE and EZB while for β = 0.1% and α = 99.9%, it is 7 times faster. This shows that ART becomes more and more advantageous over existing schemes when the required reliability increases. Third, for all schemes, the estimation time increases as the required reli￾ability increases because more number of rounds are needed to achieve the required reliability. We further observe that ART’s estimation time increases at the lowest rate as the required reliability increases because its estimator has the smallest variance. We make three main observations from Figures 13 (a), (b), and (c), which show the estimation time for 5000 tags required by each scheme with the confidence interval β vary￾ing from 0.1% to 10% for different configurations of α. First, we observe that ART is faster than all estimation schemes in all these configurations. Second, for all schemes, the es￾timation time decreases as the confidence interval increases because lesser number of rounds are needed to achieve the required reliability. 6.2 Actual Reliability The subfigures in Figure 14 show the actual reliability of ART versus the number of tags for different configurations of required reliability α and confidence interval β. We observe that ART always achieves the required reliability. 7. CONCLUSIONS AND FUTURE WORK The key technical novelty of this paper is in proposing the new estimator, the average run size of 1s, for estimating RFID tag population size. Using analytical plots, we show that our estimator has much smaller variance compared to other estimators including those used in prior work. It is this smaller variance that makes our scheme faster than the pre￾vious ones. In future work, we will work on mathematically proving that our estimator has smaller variance compared to other estimators. The key technical depth of this paper is in the mathematical development of the estimation the￾ory using this estimator. Our experimental results show that our scheme ART is significantly faster than all prior RFID estimation schemes. Furthermore, both the analytical and experimental results show that the estimation of ART is in￾dependent of tag population size. In future work, we will work on mathematically proving this independence. 8. REFERENCES [1] C. Bordenave, D. McDonald, and A. Proutiere. Performance of random medium access control, an asymptotic approach. In Proc. of Int. Conf. on Measurements and Modeling of Computer Systems SIGMETRICS, 2008. [2] J.-R. Cha and I. Jae-Hyun Kim. Novel anti-collision algorithms for fast object identification in rfid system. In Proc. of Int. Conf. on Parallel and Distributed Systems, 2005. 375