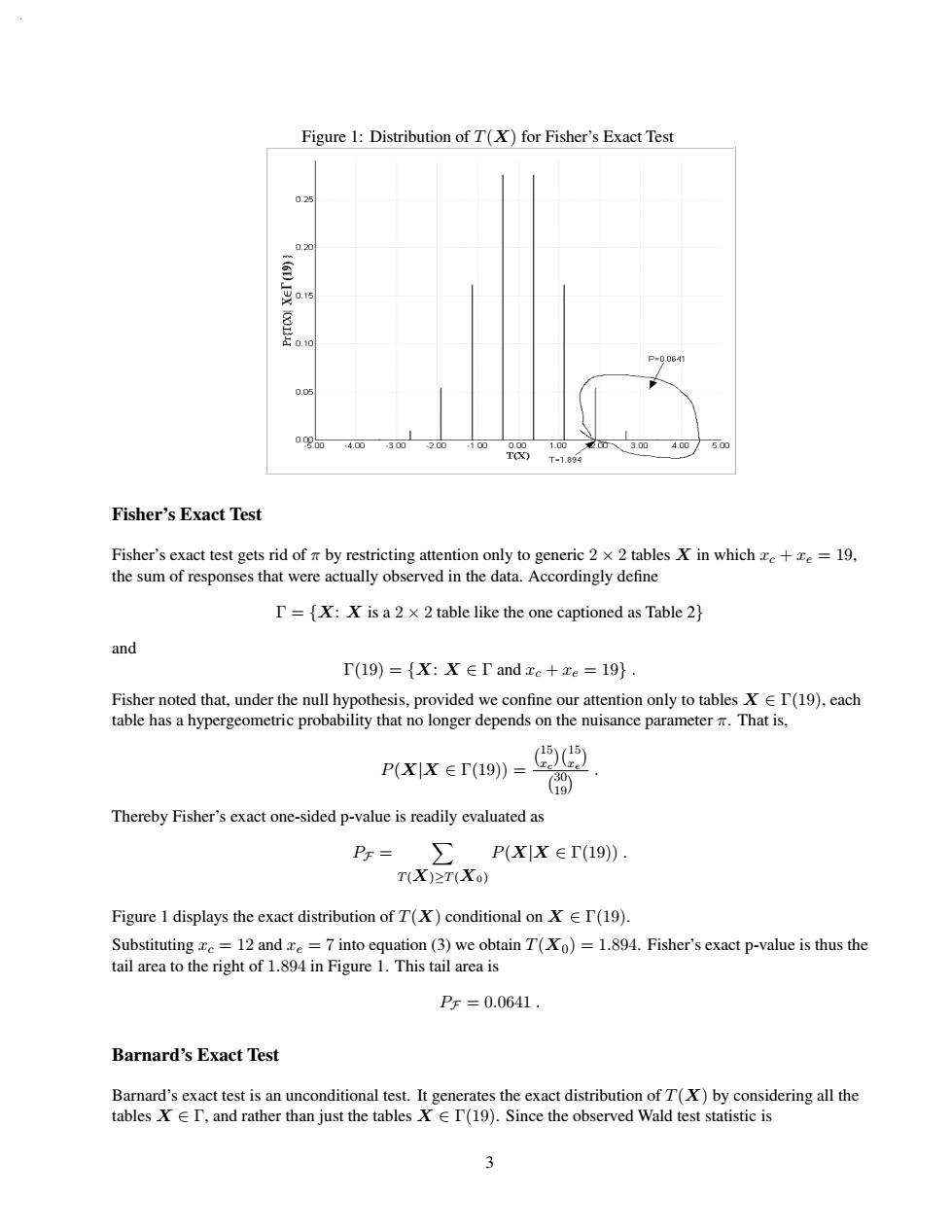
Figure 1:Distribution of T(X)for Fisher's Exact Test 0.25 0.20 0.0641 0.05 4.00 300 .0 1.00 300 4.00 5.00 T-1.894 Fisher's Exact Test Fisher's exact test gets rid of a by restricting attention only to generic 2 x 2 tables X in which e+xe =19, the sum of responses that were actually observed in the data.Accordingly define T=fX:X is a 2 x 2 table like the one captioned as Table 2} and T(19)={X:X EI and xe +xe =19). Fisher noted that,under the null hypothesis,provided we confine our attention only to tables X T(19),each table has a hypergeometric probability that no longer depends on the nuisance parameter That is, P(X|X∈T(19)= Thereby Fisher's exact one-sided p-value is readily evaluated as 王 Pr= P(X1X∈T(19). T(X)≥T(Xo) Figure 1 displays the exact distribution of T(X)conditional on X T(19). Substituting xe 12 and ze =7 into equation (3)we obtain T(Xo)=1.894.Fisher's exact p-value is thus the tail area to the right of 1.894 in Figure 1.This tail area is PF=0.0641. Barnard's Exact Test Barnard's exact test is an unconditional test.It generates the exact distribution of T(X)by considering all the tables X I,and rather than just the tables X EI(19).Since the observed Wald test statistic is 3Figure 1: Distribution of T(X) for Fisher’s Exact Test Fisher’s Exact Test Fisher’s exact test gets rid of π by restricting attention only to generic 2 × 2 tables X in which xc + xe = 19, the sum of responses that were actually observed in the data. Accordingly define Γ = {X: X is a 2 × 2 table like the one captioned as Table 2} and Γ(19) = {X: X ∈ Γ and xc + xe = 19} . Fisher noted that, under the null hypothesis, provided we confine our attention only to tables X ∈ Γ(19), each table has a hypergeometric probability that no longer depends on the nuisance parameter π. That is, P(X|X ∈ Γ(19)) = 15 xc 15 xe  30 19  . Thereby Fisher’s exact one-sided p-value is readily evaluated as PF = T(X)≥T(X0) P(X|X ∈ Γ(19)) . Figure 1 displays the exact distribution of T(X) conditional on X ∈ Γ(19). Substituting xc = 12 and xe = 7 into equation (3) we obtain T(X0)=1.894. Fisher’s exact p-value is thus the tail area to the right of 1.894 in Figure 1. This tail area is PF = 0.0641 . Barnard’s Exact Test Barnard’s exact test is an unconditional test. It generates the exact distribution of T(X) by considering all the tables X ∈ Γ, and rather than just the tables X ∈ Γ(19). Since the observed Wald test statistic is 3