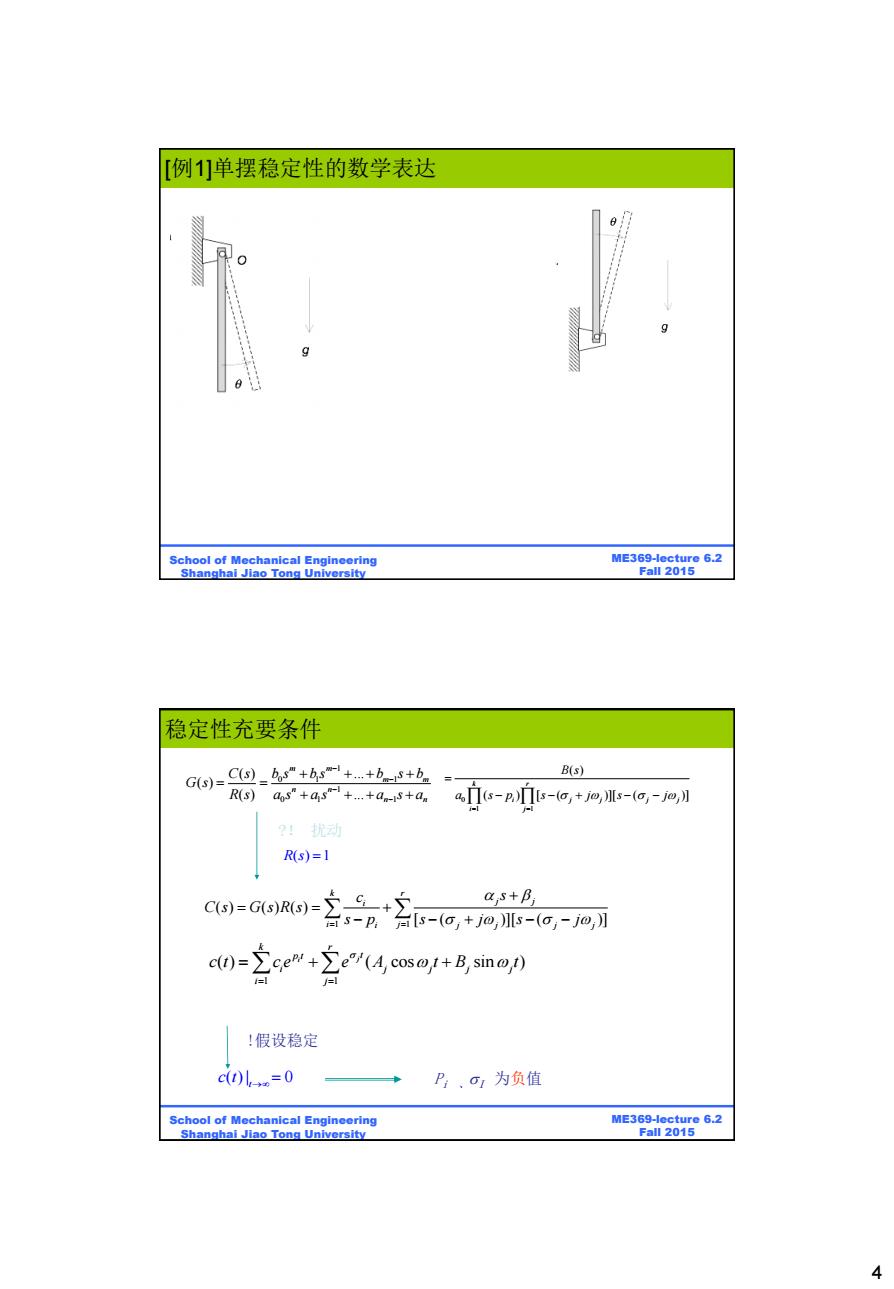
[例1]单摆稳定性的数学表达 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 稳定性充要条件 G6)=C-+hs-++b8+b B(s) R(s)aos"+as"+.+as+a a广s-p-o,+jo,s-(o,-jm,】 2!动 R(s)=1 a,s+B C()-G(S)R(s)ps=(a.+io.s=(a.-o c()(cos+B,sin) 人 !假设稳定 c()l=0 P:、o1为负值 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 44 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1]单摆稳定性的数学表达 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Pi 、I 为负值 !假设稳定 1 1 ( ) ( ) ( ) [ ( )][ ( )] k r j j i i j i j j j j c s C s G s R s s p s j s j                    1 1 ( ) ( cos sin ) j i k r p t t i j j j j i j c t c e e A t B t           ?！ 扰动 R s( ) 1  ( ) | 0 t c t   0 1 1 ( ) ( ) [ ( )][ ( )] k r i j j j j i j B s a s p s j s j               1 0 1 1 1 0 1 1 ( ) ... ( ) ( ) ... m m m m n n n n C s b s b s b s b G s R s a s a s a s a               稳定性充要条件