ME369-系统模型、分析与控制 6.2系统稳定性 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 T引例1]稳定性(Stability)定义 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 1
1 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 6.2 系统稳定性 ME369-系统模型、分析与控制 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [引例1]稳定性(Stability)定义

[引例2]稳定性定义 Tacoma narrows bridge 华盛顿州塔科马峡谷的大桥 Built July Ist,1940 Nov7h,1940 5 seconds School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fal12015 引例3稳定性定义 R(s) E(s) G(s) C(s) C(s)=_ G(s) R(s)1-G(s)H(s) H(s) G(s)=5H(s)=0.1 ()=1 G(s)=10 H(s)=0.1 r)=1 G(s)=5 H(s)=0.2 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 2
2 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Tacoma narrows bridge 华盛顿州塔科马峡谷的大桥 Built : July 1st ,1940 Nov 7th , 1940 [引例2]稳定性定义 5 seconds ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) ( ) ( ) 1 ( ) ( ) C s G s R s G s H s G s( ) 5 H s( ) 0.1 r t( ) 1 G s( ) 10 H s( ) 0.1 G s( ) 5 H s( ) 0.2 r t( ) 1 [引例3]稳定性定义
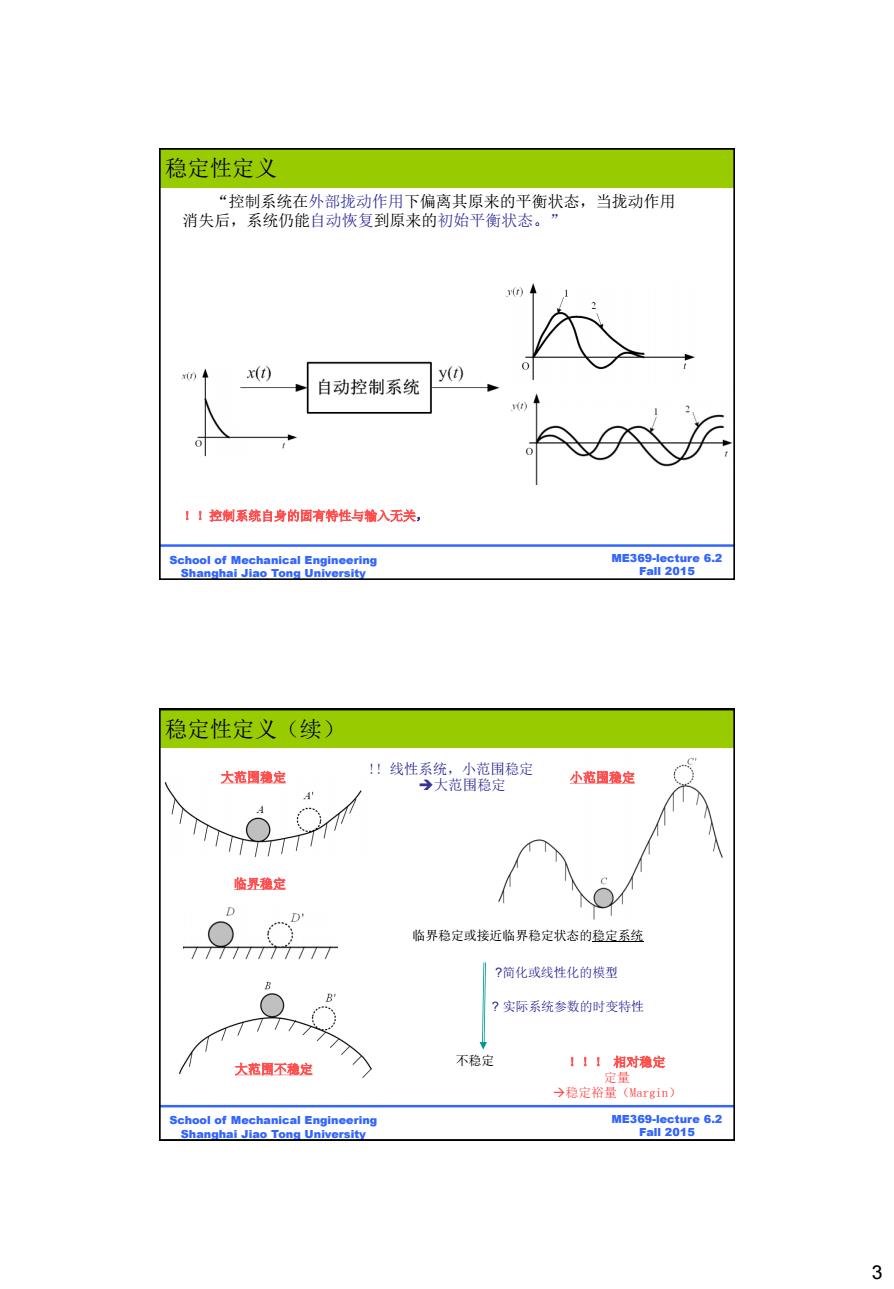
稳定性定义 “控制系统在外部拢动作用下偏离其原来的平衡状态,当拢动作用 消失后,系统仍能自动恢复到原来的初始平衡状态。” v(r) x(t) y(t) 自动控制系统 11控制系统自身的固有特性与输入无关, School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 稳定性定义(续) 大花圆稳定 !线性系统,小范围稳定 →大范围稳定 小范围稳定 临界稳定 D D 临界稳定或接近临界稳定状态的稳定系统 7TT777T777T ?简化或线性化的模型 ?实际系统参数的时变特性 77 大花圆不糖定 入 不稳定 1【1相对稳定 定量 →稳定裕量(Margin) School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 3
3 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University “控制系统在外部拢动作用下偏离其原来的平衡状态,当拢动作用 消失后,系统仍能自动恢复到原来的初始平衡状态。” !!控制系统自身的固有特性与输入无关, 稳定性定义 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 大范围稳定 小范围稳定 !! 线性系统,小范围稳定 大范围稳定 大范围不稳定 临界稳定 !!! 相对稳定 定量 稳定裕量(Margin) ?简化或线性化的模型 ? 实际系统参数的时变特性 不稳定 临界稳定或接近临界稳定状态的稳定系统 稳定性定义(续)
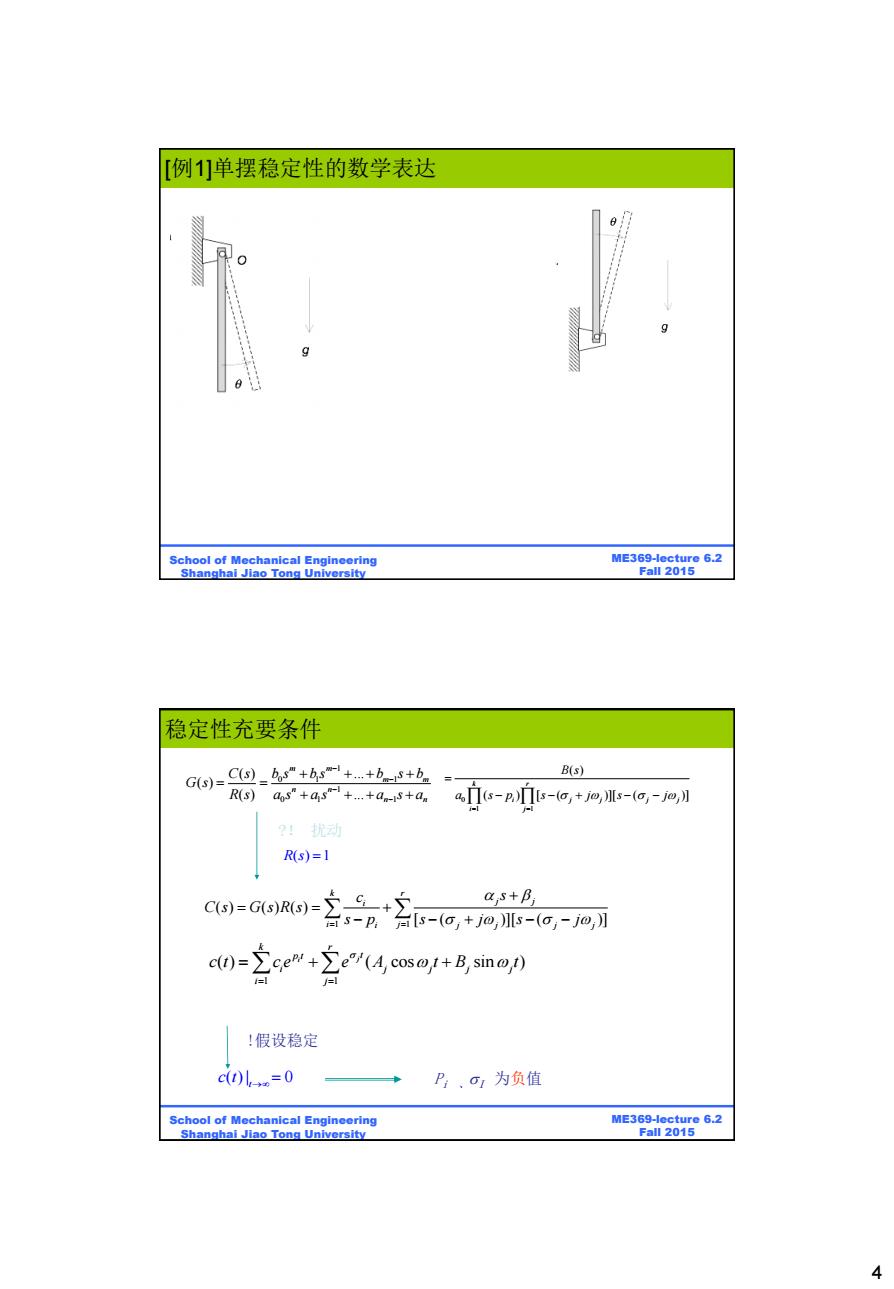
[例1]单摆稳定性的数学表达 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 稳定性充要条件 G6)=C-+hs-++b8+b B(s) R(s)aos"+as"+.+as+a a广s-p-o,+jo,s-(o,-jm,】 2!动 R(s)=1 a,s+B C()-G(S)R(s)ps=(a.+io.s=(a.-o c()(cos+B,sin) 人 !假设稳定 c()l=0 P:、o1为负值 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 4
4 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1]单摆稳定性的数学表达 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Pi 、I 为负值 !假设稳定 1 1 ( ) ( ) ( ) [ ( )][ ( )] k r j j i i j i j j j j c s C s G s R s s p s j s j 1 1 ( ) ( cos sin ) j i k r p t t i j j j j i j c t c e e A t B t ?! 扰动 R s( ) 1 ( ) | 0 t c t 0 1 1 ( ) ( ) [ ( )][ ( )] k r i j j j j i j B s a s p s j s j 1 0 1 1 1 0 1 1 ( ) ... ( ) ( ) ... m m m m n n n n C s b s b s b s b G s R s a s a s a s a 稳定性充要条件

稳定性充要条件(续) Iff condition The poles of characteristic equation have negative real part 系统特征方程的根全部具有负实部 D(s)=a(s-p,)s-(G,+j0,s-(o,-jo,】=0 →闭环系统的极点全部在s平面左半部 x平面 0 (稳定) (不稳定) →稳定性与零点无关 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fal12015 [例1]稳定性充要条件 K 单位反馈系统 G(s)= (K>0,T>0) 求K的取值范围 s(Ts+1) School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 5
5 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Iff condition : The poles of characteristic equation have negative real part 系统特征方程的根全部具有负实部 0 1 1 ( ) ( ) [ ( )][ ( )] 0 K r i j j j j i j D s a s p s j s j 稳定性与零点无关 闭环系统的极点全部在s平面左半部 稳定性充要条件(续) ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) ( 1) K G s s Ts 单位反馈系统 [例1]稳定性充要条件 ( 0, 0) K T 求K的取值范围

稳定性充要条件一Matlab求解 roots(den) 求取多项式的根 D(S)=s5+6s4+2s3+3s2+25+6 c= -5.7375 den=[162326]: -0.6922+0.7650i -0.6922-0.7650i c=roots(den) 0.5609+0.8173i 0.5609-0.8173i School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fal12015 稳定性必要条件 characteristic equation 系统特征方程 D(s)=aos"+a s"+...+as+a=0 characteristic poles D、2、…、Pr1Pa 系统特征根 及=←2p 各根之和 =1 Iff =-'2pp, 每次取两根乘积之和 condition a -)∑P,P,P.每次取三根乘彩 =(-IΠp, 各根之积. a 稳定性必要条件:系统特征各项系数具有相同的符号,且无零系数 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 6
6 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 5 4 3 2 D s s s s s s ( ) 6 2 3 2 6 roots(den) 求取多项式的根 den=[1 6 2 3 2 6]; c=roots(den) c = -5.7375 -0.6922 + 0.7650i -0.6922 - 0.7650i 0.5609 + 0.8173i 0.5609 - 0.8173i 稳定性充要条件—Matlab 求解 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 0 1 1 ( ) ... 0 n n D s a s a s a s a n n p1、p2、…、pn-1、pn 1 1 0 1 ( 1) n i i a p a 2 2 0 2 ( 1) n i j i a p p a 3 3 0 3 ( 1) n i j k i a p p p a 0 1 ( 1) n n n i i a p a 各根之和 每次取两根乘积之和 每次取三根乘积之和 各根之积 Iff condition 稳定性必要条件: 系统特征各项系数具有相同的符号,且无零系数 characteristic poles 系统特征根 characteristic equation 系统特征方程 稳定性必要条件

[例2]稳定性必要条件 如图液位控制系统,如何选取区,T以确保系统的稳定性。 0 用水开关 School of Mechanical Engineering ME369-lecture 6.2 Shanghal Jiao Tong University Fall 2015 劳斯判据(Routh's Stability Criterion)-劳斯阵列 D(s)=aos"+as"+..+an-is+a,=0 aa3a4… 4143a5. 5-2 a0a21 b1=- aa b2=- 5 GC2C3… a a 5 add2d,… 52 e 无 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 7
7 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 如图液位控制系统,如何选取K,Tm 以确保系统的稳定性。 [例2]稳定性必要条件 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 0 1 1 ( ) ... 0 n n D s a s a s a s a n n 1 1 3 0 2 1 a | a a a a | b 1 1 5 0 4 2 a | a a a a | b 1 2 3 4 2 1 0 n n n n n s s s s s s s s 024 1 3 5 a a a a a a 1 2 3 b b b 1 2 3 1 2 3 1 2 1 1 c c c d d d e e f g 劳斯判据(Routh’s Stability Criterion)--劳斯阵列

劳斯判据-充要条件 第一列符号改变次数 =系统特征方程含有正实部根的个数 a a3a4… a 43 as … 充要条件: 5-2 b ba b 劳斯阵列第一列元素不改变符号 s-3 9 C3… 5-3 dd d3… a6>0 s e e2 充要条件, 万 劳斯阵列表中第一列的各数均大于零 50 81 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 [例3]劳斯判据 D(s)=54+2s3+3s2+4s+5 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 8
8 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 充要条件: 劳斯阵列第一列元素不改变符号 第一列符号改变次数 == 系统特征方程含有正实部根的个数 2 4 1 3 5 2 2 3 3 2 3 3 2 3 2 2 1 0 0 1 1 1 1 1 1 1 n n n n n a a s a a s a a s b b c b c d s c s d d s e s f s g e a0 > 0 劳斯判据--充要条件 充要条件: 劳斯阵列表中第一列的各数均大于零 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 4 3 2 D s s s s s ( ) 2 3 4 5 [例3]劳斯判据

[例4]劳斯判据一特殊情况1 D(s)=s+s3+3s2+3s+2 ME369-lecture 6.2 Fall 2015 [例5]劳斯判据一特殊情况2 D(s)=s3+s4+5s3+5s2+6s+6 156 6 15 s 000 s2 s 0 s° x-ju ? s平面有对称分布的根 5u2=j 5,4=±j5 S3=-1 ME369-lecture 6.2 Shanghal Jiao Tong University Fall 2015 9
9 ME369-lecture 6.2 Fall 2015 4 3 2 D s s s s s ( ) 3 3 2 [例4]劳斯判据—特殊情况1 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 5 4 3 2 D s s s s s s ( ) 5 5 6 6 5 4 3 2 1 0 1 5 6 1 5 6 000 s s s s s s e s平面有对称分布的根 ? 1,2 s j 2 3,4 s j 3 5 s 1 [例5]劳斯判据—特殊情况2

[例6]劳斯判据一相对稳定必性 试判断系统有几个特征方程根位于与虚轴平行的直线一-1的右侧。 D(s)=s3+7s2+14s+22=0 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 [讨论]系统阶次与稳定性 D(s)=aos"+as"+...+as+a=0 (a>0) 1st order system a>0 a4>0 (necessary condition) 一阶系统 2nd order system a>041>0a2>0 (necessary condition) 二阶系统 3rd order system -a>04>0a,>0a3>0 (necessary condition) 三阶系统 aaz >aas 4th order system a>0a>0 a,>0a3>0a4>0 四阶系统 (necessary condition) aaas aa +aas School of Mechanical Engineering ME369-lecture 6.2 Shanghal Jiao Tong University Fall 2015 10
10 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 3 2 D s s s s ( ) 7 14 22 0 试判断系统有几个特征方程根位于与虚轴平行的直线s=-1的右侧。 [例6]劳斯判据—相对稳定必性 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 st order system 一阶系统 1 0 1 1 ( ) ... 0 n n D s a s a s a s a n n 0 ( 0) a 0 (necessary condition) a 0 1 a 0 0 a 0 1 a 0 2 a 0 0 a 0 1 a 0 2 a 0 3 a 0 1 2 0 3 a a a a 0 a 0 1 a 0 2 a 0 3 a 0 2 2 1 2 3 0 3 1 4 a a a a a a a 4 a 0 [讨论]系统阶次与稳定性 2 nd order system 二阶系统 3 rd order system 三阶系统 4 th order system 四阶系统 (necessary condition) (necessary condition) (necessary condition)