ME369课后作业5# Fall 2015 提交截止日期:2015-12-09(周三) 学号: 姓名: 第一题某质量-弹簧-阻尼系统10r+c+20x=f),输入为f0)=11cos(o0),求得c,使 后rwn更,5,5六 得x最大稳态幅值不大于华·2 20 5之7叨时(%c2o)元孩,氯场顶=。K3 A()二F% ① M%三k5列r元 Mw八r1≤3 0 eP,a7o7)0月向若拔 f tg6?=ye1)260 5<o7o7 0:②2C之2:6 第二题二阶系统式+2和,i+ox=f),图示为对应的输入波形和稳态输出。求取无阻尼 固有频率和阻尼比。 =顺象疙 f( 图预n练快n36了=时 W二Wn 孕脉T二45Mw子sr4 (t) 由星联文+2S∽文t哈不=, 气房人)=3+25hstu2 201 →F(w-w1+j% |wwzun三2wn 岁妇二首子花W=n时 安应细也可臂 由原知14johem品 =9了20,02
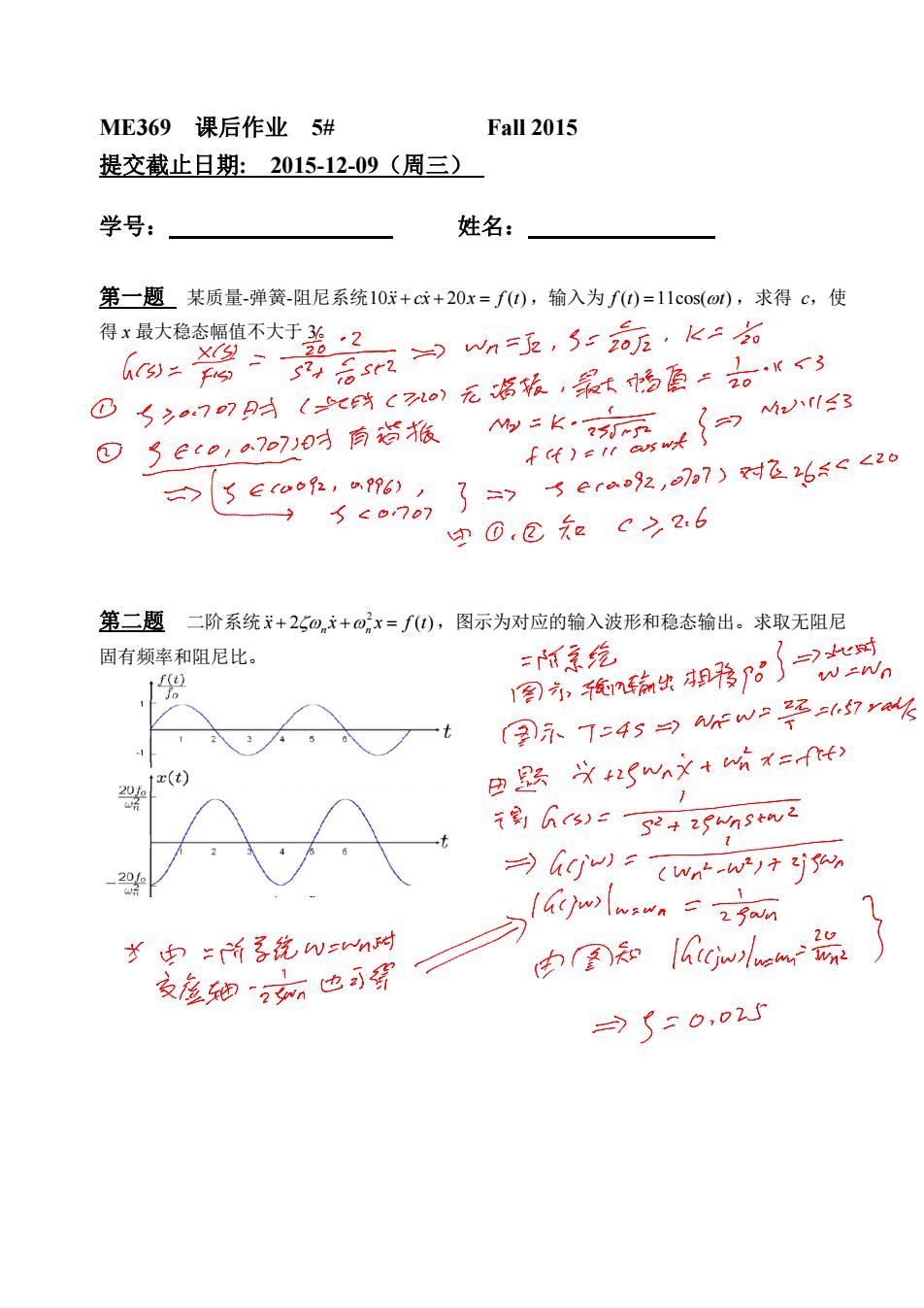
ME369 课后作业 5# Fall 2015 提交截止日期: 2015-12-09(周三) 学号: 姓名: 第一题 某质量-弹簧-阻尼系统10 20 ( ) x cx x f t ,输入为 f ( ) 11cos( ) t t ,求得 c,使 得 x 最大稳态幅值不大于 3。 第二题 二阶系统 2 2 () n n x x x ft ,图示为对应的输入波形和稳态输出。求取无阻尼 固有频率和阻尼比

第三题设单位反馈控制系统的开环传递函数 Gs)=10 5+1,当系统输入信号 r)=2cos(21-45)作用下,试求系统的稳态输出。 1王w)= i12xw4 豆0‘品到品 ∠0=-ran Yf)=At+之4-。lA,mnfr+上] 2知A=2,W=2m459。e9。°+45)=4s° 时(委gl=o99乙)=030 7有cd=76snc2大+47) 或x1k-e=7gcc大-53y 第四题_绘制下列传递函数的幅相频率特性 1 (1)G(s)= (2)G(s)= (s+1)(s+3) 5s+1)(s+3V (9w)-22w2w w4w2(2-)2 w学o 以 Wo Vw)-Imldo-]=o >W4a1 wf uwfe:lag
第三题 设单位反馈控制系统的开环传递函数为 1 10 ( ) s G s ,当系统输入信号 r(t) 2cos(2t 45) 作用下,试求系统的稳态输出。 第四题 绘制下列传递函数的幅相频率特性 (1) ( 1)( 3) 1 ( ) s s G s (2) ( 1)( 3) 1 ( ) s s s G s
第五题 已知最小相位系统的波德图,试求出系统的传递函数. L( 3(F1) C3浅门 20b dB ] 1xf(9 40dB/dee 20 k5 -20dB/dee 6: Stol 0.1 -40dB/dec 92(5H) (a) to CZs) L(o)年 G6) KC25{) dB (?S+)(1sH) ?6 (vs()CO SRi) 20 -20dB/dec 2=2n=⑦ -40dB/dee 0.5 0.050.1 -20dB/dee (b) k G)=s(孟0(&” 2 L() LW1,s)中 0-440 w二o、 dB -20dB/dec css-ywr 7W2” 40 C5,W2)中-20- -40 40dB/dec (SwL19s k÷。 2 -12 C口,W门中,6 L9i52”5四太:744:epr6,国.含 中净东和w%=3%=)h=片wy二s2么 252 2740口 s(?43狐4+27o4)
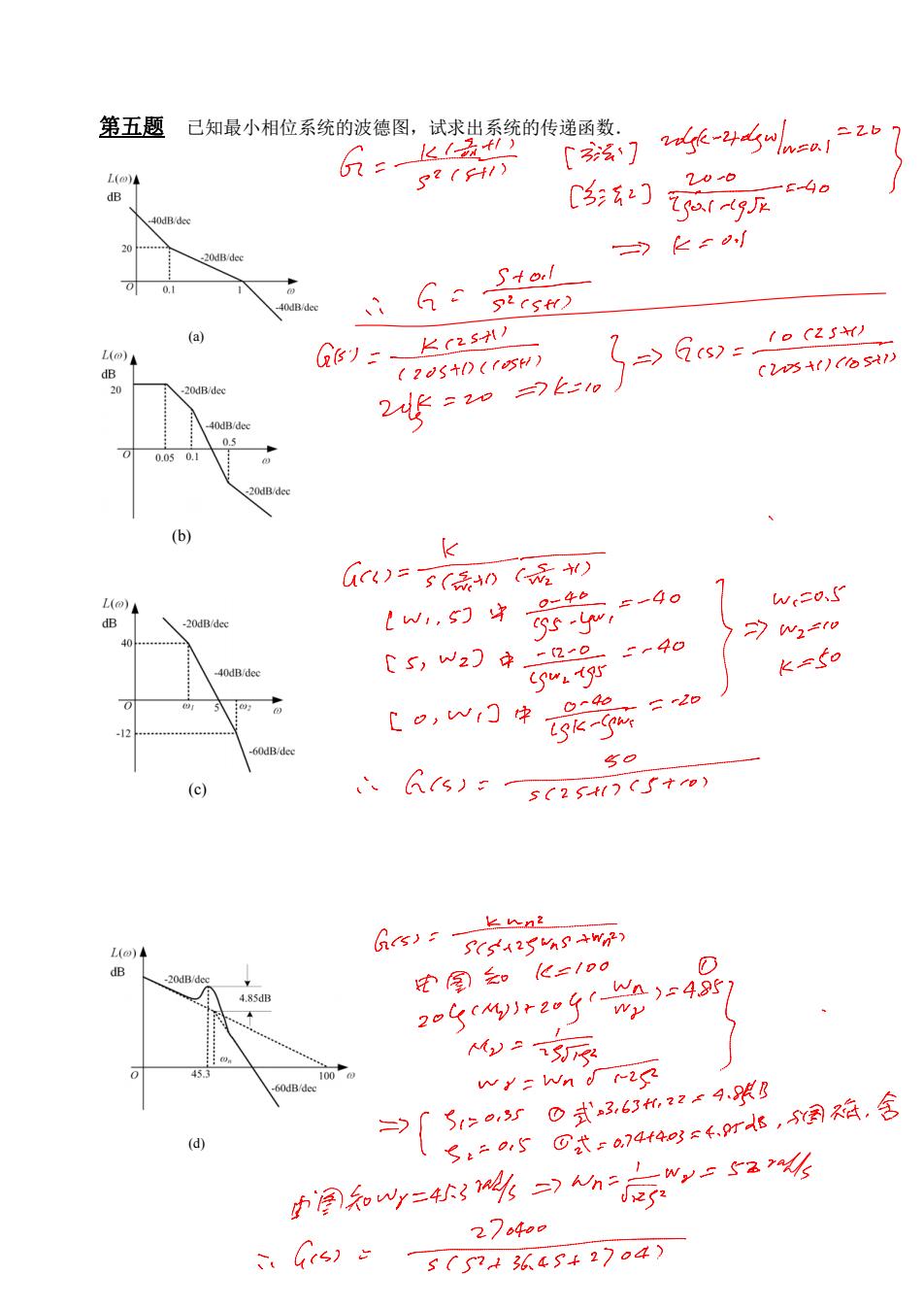
第五题 已知最小相位系统的波德图,试求出系统的传递函数. (a) (b) (c) (d)
第六题 设单位反馈系统如图所示.其中无阻尼自然频率0,=90rd/s,阻尼比5=0.2.试 分别用下述方法确定速度常数K值为多大时,系统是稳定的.分别在尼奎斯特图和波德图上 应用尼奎斯特判据 R(s) C(s) +2女。+ 上 ∠20 w=。) wEwA VCw)0 、3 wnc会) 6K636@ g6→o<k<3t
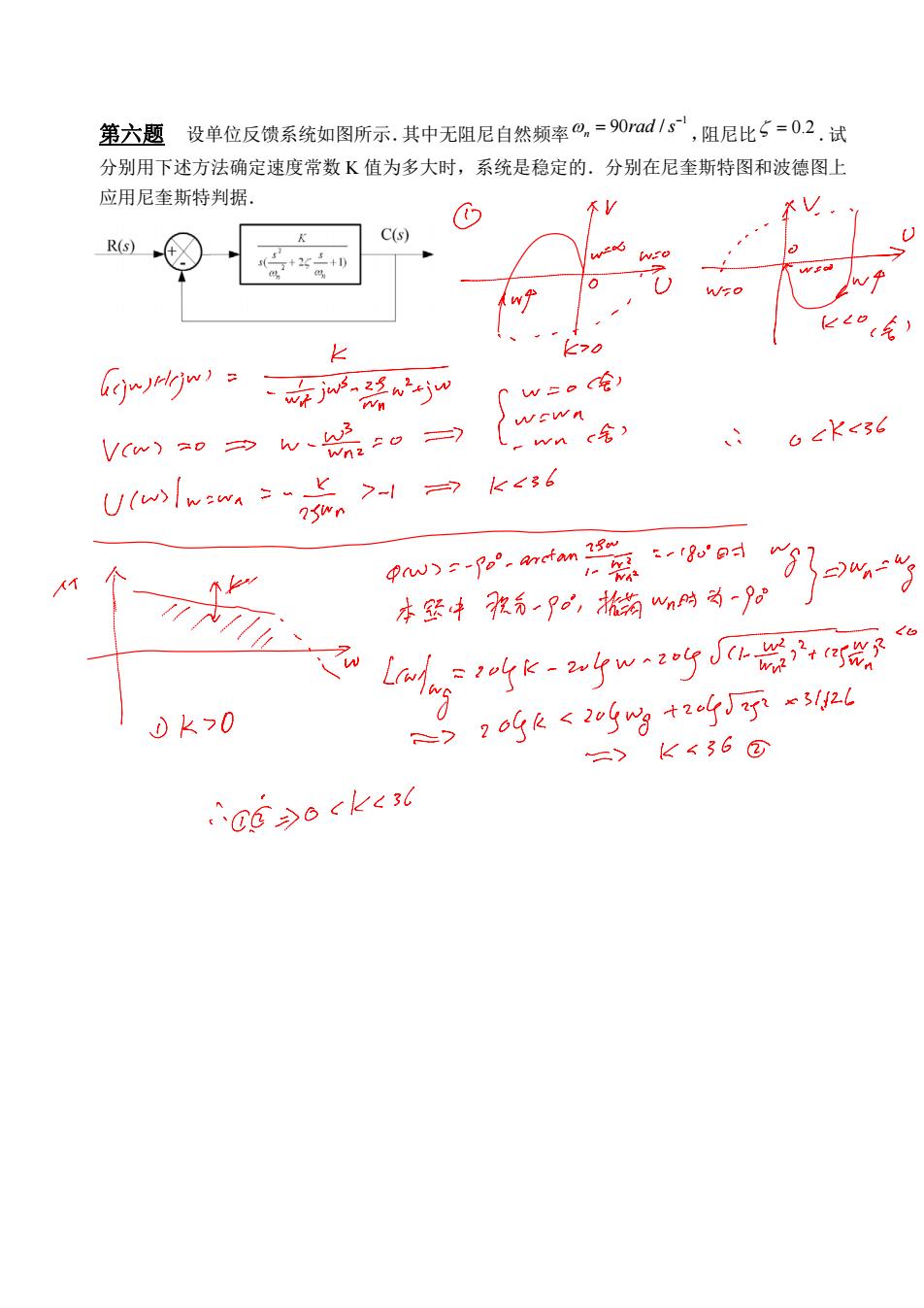
第六题 设单位反馈系统如图所示.其中无阻尼自然频率 1 90 / n rad s ,阻尼比 0.2.试 分别用下述方法确定速度常数 K 值为多大时,系统是稳定的.分别在尼奎斯特图和波德图上 应用尼奎斯特判据.

2e-7 G(s)H(s)=- 第七题有开环传递函数为 (s+1(0.5s+),的闭环系统,试利用尼奎斯特判据 确定系统稳定时T的最大值 个V 与长爱④自支,e台在,A充京早为UV 转唯式泽,一)单2四+永元 Liwlwcwe=o人3 二1 →1,aew gwe+25w9tw2-4=0 CK37风水 c=e3,we-乙6u发 c凭) 9w)w:we7-180 ap -(po tardanw iaean onsw ts7.3w7 wrwe 之7≤,74s
第七题 有开环传递函数为 ( 1)(0.5 1) 2 ( ) ( ) s s s e G s H s sT ,的闭环系统,试利用尼奎斯特判据 确定系统稳定时 T 的最大值.

第八题设系统开环对数幅频特性如图所示,图中0和,为转角频率,为增益交界频率, v为积分环节数,试导出用0和2表示的关于最大相位裕量时的”c表达式,并确定v=1时的 最大相位裕量, L(o)◆ -20v dB/dec -20 dB/dec :及果抽匠统 20v dB/dec 2=80+∠rkt G)w)1)= (jw)(j jw)uijw)=pvtv arctencan( 20 w, =>(V- W2,=(V-()w好w M224w2 vEl,D=p.o Vi,w年W2,(
第八题 设系统开环对数幅频特性如图所示,图中1和2 为转角频率,c 为增益交界频率, v 为积分环节数,试导出用1和2 表示的关于最大相位裕量时的c 表达式,并确定v 1时的 最大相位裕量.