上海交通大学：《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[17]Lecture92-design of control system in state space 控制系统的状态空间设计

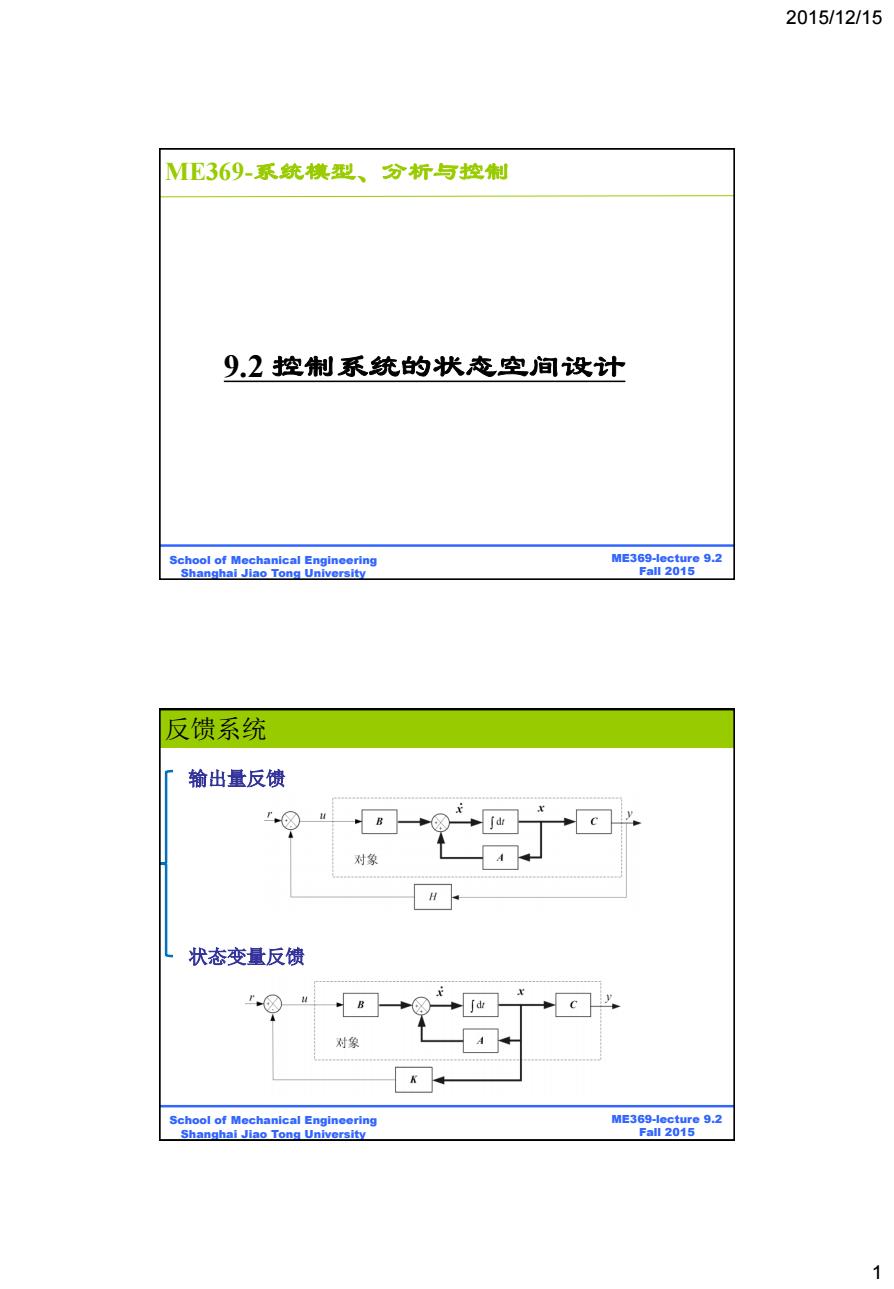
2015/12/15 ME369-系统模型、分析与控制 9.2控制系统的状态空间设计 School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fal12015 反馈系统 输出量反馈 对象 状态变量反馈 B 对象 School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 1

2015/12/15 1 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 9.2 控制系统的状态空间设计 ME369-系统模型、分析与控制 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 反馈系统 状态变量反馈 输出量反馈

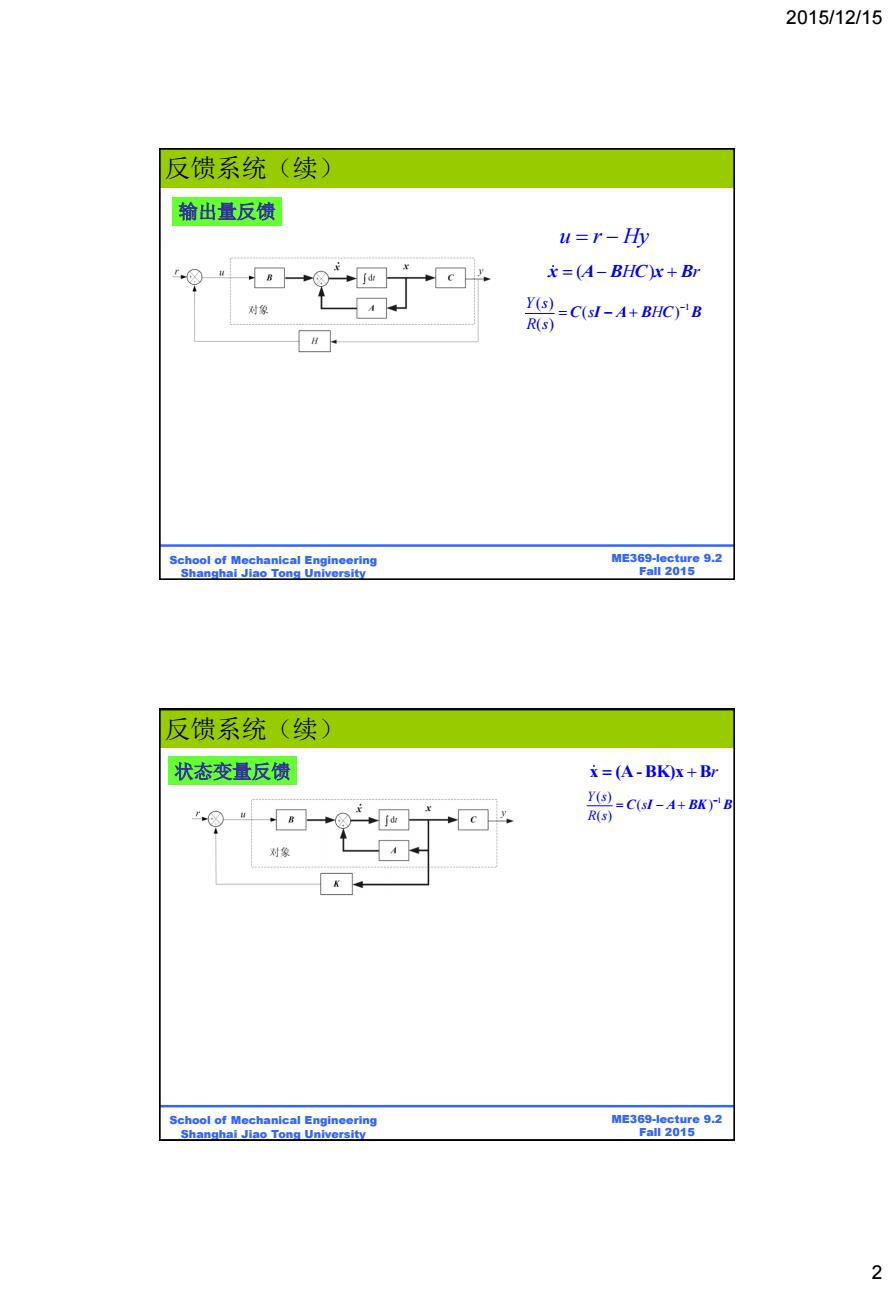
2015/12/15 反馈系统（续） 输出量反馈 u=r-Hy 文=(A-BHC)x+B 对象 Y(s)=C(sI-A+BHC)B R(s) H School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 反馈系统（续） 状态变量反馈 =(A-BK)x+Br Y(s)-C(sI-A+BK)B R(s) 对象 School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 2

2015/12/15 2 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 反馈系统（续） u r Hy   x A B C x B    ( ) H r1 ( ) ( ) ( ) Y s s H R s     C I A B C B 输出量反馈 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 反馈系统（续） x (A - BK)x B   r 1 ( ) ( ) ( ) Y s s R s     C I A BK B 状态变量反馈

2015/12/15 极点配置(Pole Placement) Y(s)=C(sI-A+BK)B R(s) 1I-(A-BK=0 sI-(A-BK)=0 (2-)2-2)…(2-)=0 (s-S)s-S2)…(s-Sn)=0 School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 例1]极点配置 0 1 0 X 0 状态反馈后配使极点为 0 0 + 0 2=-2±j4 -5 -6Lx1 S3=-10 School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 3

2015/12/15 3 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 极点配置（Pole Placement） 1 2 ( ) 0 ( )( ) ( ) 0 n                  I A BK 1 ( ) ( ) ( ) Y s s R s     C I A BK B 1 2 | ( ) | 0 ( )( ) ( ) 0 n s s s s s s s           I A BK ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University u x x x x x x                                              1 0 0 1 5 6 0 0 1 0 1 0 3 2 1 3 2 1    s1,2  2  j4 s3  10 状态反馈后配使极点为 [例1]极点配置

2015/12/15 状态观测器 通过控制量和测得的输出量，估计状态变量 元=A+Bu y=C =A+Bu+G(y-j) 对象 =A+Bu+GC(x-) =(A-GC)元+Bu+Gy G 文-元=Ar+Bu-[(A-GC)R+B+Gy B+③ jd山 =(A-GC)x-) 状态观测器 x-=e4cr(x-元) 「I-(A-GC)=0 sI-(A-GC)0 (2-2)2-22)…(2-1n)=0 (s-5s-52)…(s-sn)=0 School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 例2]状态观测器设计 -3 设计一个全阶状态观测器，其期望特性值为 =-1.8+j2.4 y=[0x 元2=-1.8-j2.4 School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 4

2015/12/15 4 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 状态观测器 -通过控制量和测得的输出量，估计状态变量 x Ax B   u y  Cx ( ) ( ) ( ) u y y u u y             x Ax B G Ax B GC x x A GC x B G [( ) ] ( )( )        u u y    x x Ax B A GC x B G A GC x x ( ) 0 0 ( ) t e     A GC x x x x 1 2 ( ) 0 ( )( ) ( ) 0 n  GC                 I A 1 2 | ( ) | 0 ( )( ) ( ) 0 n s GC s s s s s s           I A ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University   0 20.6 0 1 0 1 0 1 u y                x x x 设计一个全阶状态观测器，其期望特性值为 1     1.8 2.4 j 2    1.8 2.4 j [例2]状态观测器设计

2015/12/15 基于状态观测器的状态量反馈 对象 状方观料法 T-ce School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 例3]基于状态观测器的状态变量反馈 b 要求 5k1,2=-7.07±7.07 y=[0]x 5g2=-50 School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 5

2015/12/15 5 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 基于状态观测器的状态量反馈 r                              x x B x A BK GC A GC BK x B y  0        x C x 1 0 0 0                                   I A BK I A BK BK I I GC A GC BK I I A GC ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 0 1 0 0 5 100 u               x x y  1 0 x 要求 sk1,2  7.07  j7.07 sg1,2  50 [例3]基于状态观测器的状态变量反馈

2015/12/15 [Matlab]状态空间表达 文=Ax+Bu ss(A,B,C,D) y=Cx+Du a= xl x2 x101 x252 b= ul x10 x23 .0 1 c= xl x2 y101 d= y=[01]x ul y10 ss[01-5-2].[0,3],[01],0) Continuous-time model. School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 [Matlab]模型转换 num(s) =C(sI-A)B+D den(s) [num,den]=ss2tf(A,B,C,D,iu) [A,B,C,D]=tf2ss(num,den) k(s-=(DXs-=(2))(s-=(m))=C(sI-A)B+D (s-p1)s-p2)…(s-p(n) [z,p,k]=ss2zp(A,B,C,D,iu) [A,B,C,D]=zp2ss(z,p,k) School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 6

2015/12/15 6 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [Matlab]状态空间表达 ss([0 1;-5 -2],[0;3],[0 1],0) a = x1 x2 x1 0 1 x2 -5 -2 b = u1 x1 0 x2 3 c = x1 x2 y1 0 1 d = u1 y1 0 Continuous-time model. x   Ax  Bu y  Cx  Du ss(A,B,C,D) 0 1 0 [ ] [ ] 5 2 3   u   x x y [0 1]x ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [z,p,k]=ss2zp(A,B,C,D, iu)  C I  A B  D 1 ( ) ( ) ( ) s den s num s [num,den]=ss2tf(A,B,C,D,iu)  C I  A B  D       1 ( ) ( (1))( (2)) ( ( )) ( (1))( (2)) ( ( )) s s p s p s p n s z s z s z n k   [A,B,C,D]=tf2ss(num,den) [A,B,C,D]=zp2ss(z,p,k) [Matlab]模型转换

2015/12/15 Matlab]模型转换（续） s2-0.5s+2 G(s)= s2+0.4s+1 z= 0.2500+1.3919i 0.2500-1.3919i p* -0.2000+0.9798i -0.2000-0.9798i k= 1 A= -0.4000-1.0000 1.0000 0 B= 1 0 num=1-0.52 C= den=10.41: -0.90001.0000 [z.p.k]=tf2zp(num,den) D= [A.B.C.D]=tf2ss(num,den) School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fal12015 [Matlab]模型转换（续） ]-0] A=01;-25-4: B=11:01] C=1001 D=00:001: 找 [num1,den1]=ss2tfA.B.C.D.1) [num2,den2]=ss2tfA,B,C,D,2) Y(s) U(s) Y(s) U,(s) numl= 01.00004.0000 0 0-25.0000 Y() denl= 1.00004.000025.0000 U,(s) num2= 01.00005.0000 Y2(s) 01.0000-25.0000 U,(s) den2= 1.00004.000025.0000 School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 7

2015/12/15 7 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 0.4 1 0.5 2 ( ) 2 2      s s s s G s num=[1 -0.5 2]; den=[1 0.4 1]; [z,p,k]=tf2zp(num,den) [A,B,C,D]=tf2ss(num,den) z = 0.2500 + 1.3919i 0.2500 - 1.3919i p = -0.2000 + 0.9798i -0.2000 - 0.9798i k = 1 A = -0.4000 -1.0000 1.0000 0 B = 1 0 C = -0.9000 1.0000 D = 1 [Matlab]模型转换（续） ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University                                 2 1 2 1 2 1 0 1 1 1 25 4 0 1 u u x x x x   找 ( ) ( ) 1 1 U s Y s ( ) ( ) 1 2 U s Y s ( ) ( ) 2 1 U s Y s ( ) ( ) 2 2 U s Y s A=[0 1;-25 -4]; B=[1 1;0 1]; C=[1 0;0 1]; D=[0 0;0 0]; [num1,den1]=ss2tf(A,B,C,D,1) [num2,den2]=ss2tf(A,B,C,D,2) num1 = 0 1.0000 4.0000 0 0 -25.0000 den1 = 1.0000 4.0000 25.0000 num2 = 0 1.0000 5.0000 0 1.0000 -25.0000 den2 = 1.0000 4.0000 25.0000 [Matlab]模型转换（续）

2015/12/15 Matlab状态空间中动态分析函数 ①impulse(A,B,C,D) ②step(A,B,C,D) ③lsim(A,B,C,D,u,) ④bode(A,B,C,D) ⑤nyqusit((A,B,C,D) ⑥rlocus(A,B,C,D) ⑦ozmap(A,B,C,D) School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fal12015 Matlab]状态空间中系统设计 ①K=places(A,B,P) ②K=acker(A,B,P) 对偶问题(Dual problem) I文=Ax+Bu 元=AIR+CTǜ y=Cx i=BTx |sl-(A-BK)川 |sl-(A'-CG)川 School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 8

2015/12/15 8 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ①impulse(A,B,C,D) ②step(A,B,C,D) ③lsim(A,B,C,D,u,t) ④bode(A,B,C,D) ⑤nyqusit(A,B,C,D) ⑥rlocus(A,B,C,D) ⑦pzmap(A,B,C,D) [Matlab]状态空间中动态分析函数 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ①K=places(A,B,P) ②K=acker(A,B,P) | ( ) | sI A BK   | ( ) | T T s C G I A   x = Ax + Bu y  Cx ˆ ˆ ˆ T T x = A x + C u ˆ ˆ T y  B x 对偶问题（Dual problem） [Matlab]状态空间中系统设计

2015/12/15 [例4]状态空间中系统设计 0 目的 Pk12=-1.8±2.4 y=lo以 Pg1,2=-8 A=01:20.601: B=0:11: C=1,01: QC=[BA*B]: nc-可ank(QC) QO=ICA*C1 nc no=rank(QO) 2 PK=-1.8+2.4*i-1.8-2.4*ij: n0= K=acker(A,B,PK) AA=A K= BB-C; 9.60003.6000 PG=-8-81: G+ GG=acker(AA.BB,PG); 16.0000 G-GG 84.6000 School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fal12015 例5]状态空间中系统设计 目的P2=-2±j2W3 P3=p4=-10 m=0.1kg M-2kg =0.5m 77777777 A=0100,20.60000;0001:-0.490001: B=0:-1:0:0.5: K= P=-2+2*sqrt(3)*1(-2-2*sqrt3)*i-10-10 -298.1494-60.6972-163.0989-73.394 K=acker(A,B,P) School of Mechanical Engineering ME369-lecture 9.2 Shanghai Jiao Tong University Fall 2015 9

2015/12/15 9 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University u              1 0 20.6 0 0 1 x x y  1 0x 1,2 1.8 2.4 k 目的 p j    pg1,2  8 A=[0 1; 20.6 0]; B=[0;1]; C=[1,0]; QC=[B A*B]; nc=rank(QC) QO=[C' A'*C']; no=rank(QO) PK=[-1.8+2.4*i -1.8-2.4*i]; K=acker(A,B,PK) AA=A'; BB=C'; PG=[-8 -8]; GG=acker(AA,BB,PG); G=GG' nc = 2 no = 2 K = 29.6000 3.6000 G = 16.0000 84.6000 [例 4]状态空间中系统设计 ME369-lecture 9.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University m=0.1kg M=2kg l=0.5m 目的 p1,2  2  j2 3 p3  p4  10 A=[0 1 0 0;20.60 0 0 0 ;0 0 0 1;-0.49 0 0 0]; B=[0;-1;0;0.5]; P=[(-2+2*sqrt(3)*i) (-2-2*sqrt(3)*i) -10 -10]; K=acker(A,B,P) K = -298.1494 -60.6972 -163.0989 -73.394 [例 5]状态空间中系统设计