
2015/12/1 ME369-系统模型、分析与控制 8.2PD校正 School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 PID控制器 Disturbance Controller D(s) Reference Control Plant Input Error Gc(s) Input Output Gp(s) R(s) -E(s) U(s) Y(s) H(s) 比例(P)+积分(I)+微分(D) 时 :(-Ke()+Ke(dr+Kp). 频域: UG)-KKE() Gc(s) [Ko=Kc Ge()-Ke De 9 Nc(s)Kps2+Kps+KLKp(s+)s+) Kp=Kc(白+) 5 K1=Ko2 School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 1
2015/12/1 1 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 8.2 PID 校正 ME369-系统模型、分析与控制 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University PID 控制器 比例(P)+ 积分(I)+ 微分(D) 时域: 频域:
2015/12/1 例1-1] P控制 系统设计要求:1)零稳态误差;2)阶跃响应时超调量小于10%: 3)2%允许误差范围时的调整时间小于6秒。 Disturbance Ds) Reference Coutroller Plant Gp(s) Control Input + Error Input 4 Output Gc(s) R E(s) Us) (2s+100.5+1) Sensor H(s) G(s)=Kp 4 G(s).Gp(s) Kr+1X(0.5s+1) 4Kp Gp(3) 1+G.-Gr0-H阿1+K,2s+D0.5+D (2s+100.55+1)+4Kp Gp(s) 4 Gm⊙=1+Gc-G,(9-H©(2s+0.5+0+4K, School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 例1-11 P控制(续) 1.5 1.0 05 0 0.5 -1.0 -15 -2.5 -2.0-15-1.0-0.5 0.5 School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 2
2015/12/1 2 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1-1] P控制 系统设计要求:1)零稳态误差;2)阶跃响应时超调量小于10%; 3)2%允许误差范围时的调整时间小于6秒。 ( ) G s K c P BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1-1] P控制(续)
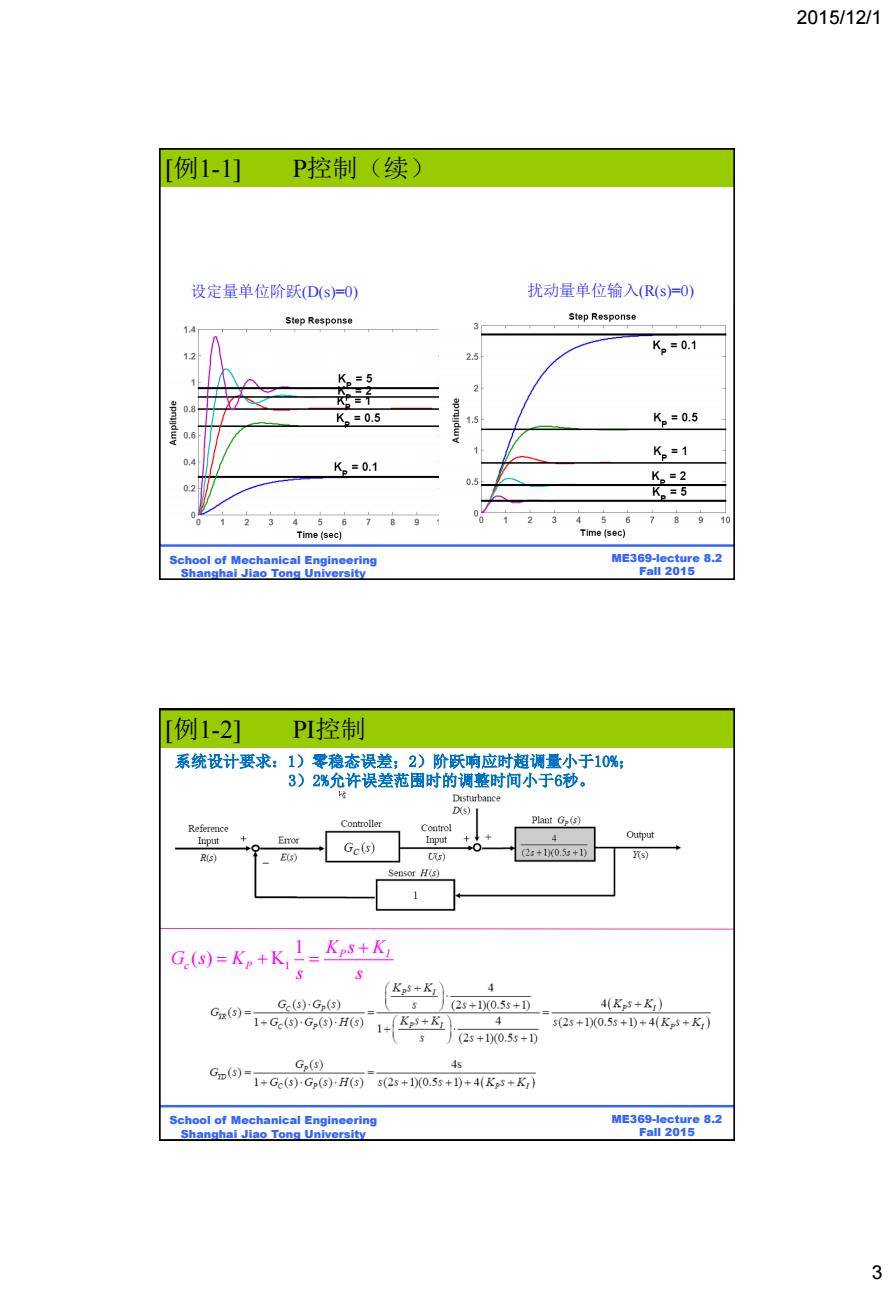
2015/12/1 T例1-11 P控制(续) 设定量单位阶跃(D(s)=O) 扰动量单位输入(R(s)=O) Step Response Step Response K2=0.1 K=5 0.8 K。=0.5 K。=0.5 0.6 K。=1 0.4 K。=0.1 K。=2 0.2 K。=5 234567891 2 3 456 7 89 10 Time(sec) Time (sec) School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 例1-2] PI控制 系统设计要求:1)零稳态误差;2)阶跃响应时超调量小于10%; 3)2%允许误差范围时的调整时间小于6秒。 Disturbance D(s)I Reference Comt山oller Control Plant Ge(s) Input Input+ 4 Output R(s) E(s) Gc(s) Us) (2s+1D(0.5x+1) s Sensor H(s) 1 1 G.(s)=Kp+K Kps+K Kos+KI 4 G(s)G(s) (25+1(0.55+1) 4(Kp3+K) G(5)= 1+G(s)G(3)H(s) 1+8+K 4 5(25+1(0.55+1)+4K-+K,) (25+10(0.55+1) G(s)= G(s) +Gc(s)-Gp(s)H(s)s(2s+10(0.5s+1)+4(Kps+,) School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 3
2015/12/1 3 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 设定量单位阶跃(D(s)=0) 扰动量单位输入(R(s)=0) [例1-1] P控制(续) BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1-2] PI控制 系统设计要求:1)零稳态误差;2)阶跃响应时超调量小于10%; 3)2%允许误差范围时的调整时间小于6秒。 I 1 ( ) K P I c P K s K G s K s s
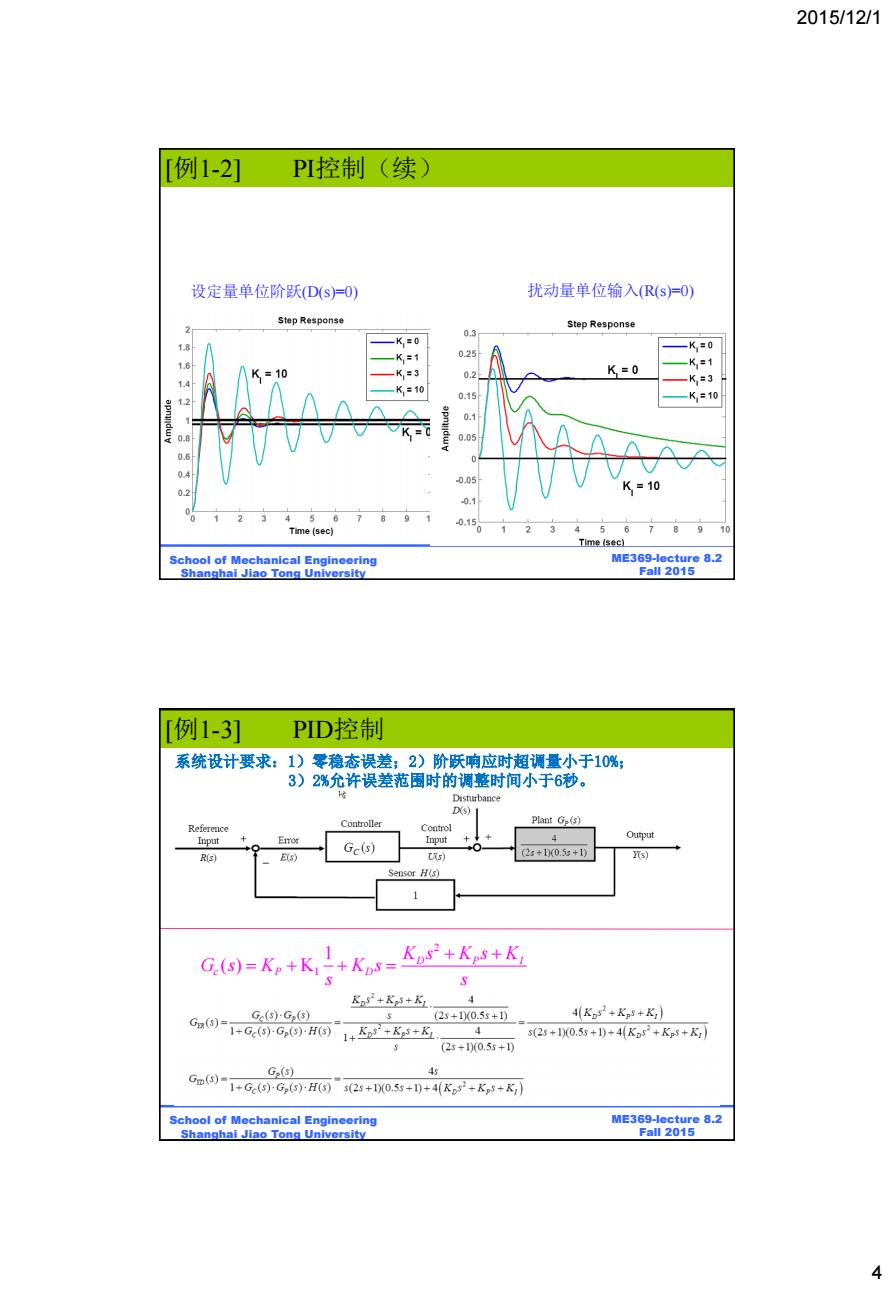
2015/12/1 T例1-21 PI控制(续) 设定量单位阶跃(D(s)=O) 扰动量单位输入(R(s)=O) Step Response Step Response 1.8 K=0 03 -K=0 K,=1 025 K=1 K=10 K=3 02 K=0 1.4 K,=3 K=10 12 K=10 0.8 0.6 0.05 0.2 K=10 0.1 015。 Time (sec) 5 6 Time (sec) School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fal12015 例1-3] PID控制 系统设计要求:1)零稳态误差;2)阶跃响应时超调量小于10%; 3)2%允许误差范围时的调整时间小于6秒。 Disturbance D(s) Reference Comt山oller Control Plant Ge(s) Input Input 4 Output E(s) Gc(s) R(s) Us) (2s+10(0.5x+1) s Sensor H(s) 1 G(s)=Kp+K-+Kps= Kos2+Kps+K Kos+Ks+K1 4 Ge(s)-G(s) (2s+1)(0.5s+1) 4K2+Kn+K) G(S)= 1+Ce(6)G,(H⑤1++K5+&. 4 s(23+100.5s+1)+4Ks2+K3+K,) (25+100.55+1) G.(s) 4 6m0)1+G.)-G,9-HOs2s+X0.5s+)+4Ko+K,5+) School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 4
2015/12/1 4 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 设定量单位阶跃(D(s)=0) 扰动量单位输入(R(s)=0) [例1-2] PI控制(续) BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University PID controller [例1-3] PID—控制example--PID 系统设计要求:1)零稳态误差;2)阶跃响应时超调量小于10%; 3)2%允许误差范围时的调整时间小于6秒。 2 I 1 ( ) K D P I c P D K s K s K G s K K s s s
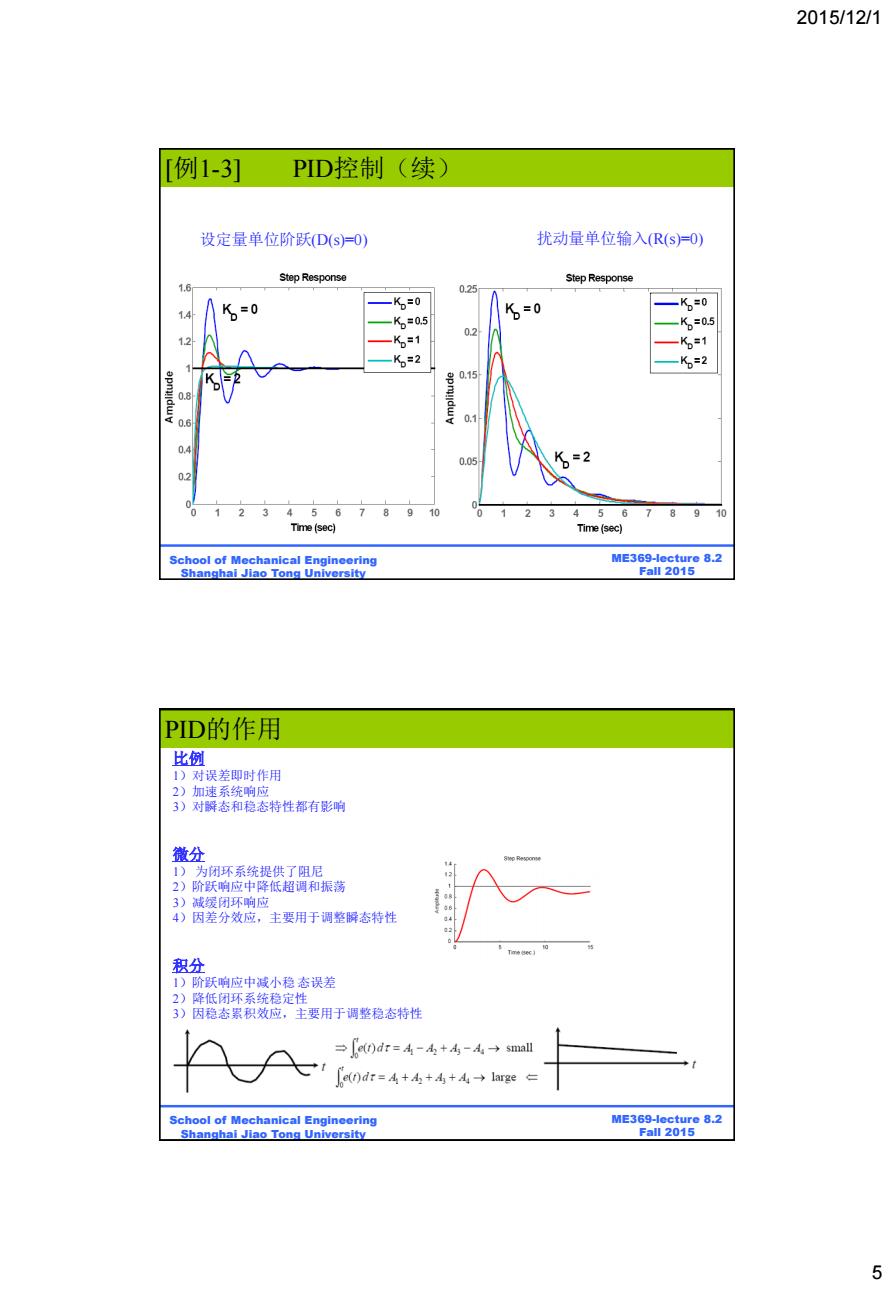
2015/12/1 T例1-3] PID控制(续) 设定量单位阶跃(D(s)=O) 扰动量单位输入(R(s)=O) Step Response Step Response 1.6 0.25 K=0 =0 0 K=0 K=0.5 K=0.5 0.2 12 X=1 K=2 K=2 0.15 0.6 0.4 0.05 K=2 0.2 0 123456 7 4 6 1 8 910 Time(sec) Time (sec) School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fal12015 PID的作用 比例 」)对误差即时作用 2)加速系统响应 3)对瞬态和稳态特性都有影响 徽分 1)为闭环系统提供了阻尼 2)阶跃响应中降低超调和振荡 3)减缓闭环响应 4)因差分效应,主要用于调整瞬态特性 积分 1)阶跃响应中减小稳态误差 2)降低闭环系统稳定性 3)因稳态累积效应,主要用于调整稳态特性 台e0dr=4-4+4-A→smal e0dr=4+4+4+4→large School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 5
2015/12/1 5 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1-3] PID控制(续) 设定量单位阶跃(D(s)=0) 扰动量单位输入(R(s)=0) BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University PID的作用 比例 1)对误差即时作用 2)加速系统响应 3)对瞬态和稳态特性都有影响 微分 1) 为闭环系统提供了阻尼 2)阶跃响应中降低超调和振荡 3)减缓闭环响应 4)因差分效应,主要用于调整瞬态特性 积分 1)阶跃响应中减小稳 态误差 2)降低闭环系统稳定性 3)因稳态累积效应,主要用于调整稳态特性

2015/12/1 频域分析-P控制 G(s) C G.(s)= U(s)=Kp E(s) H(s) L(w) 已校正 -20 -20 -40 L(@)=20lgKp 0 40 (o)◆ 校正 p.(o)=0 0° -90 -180 (@)1 K>1 →开环增益个→稳态误差↓ →aoc个过渡过程时间↓ →原系统稳定裕量充分大时才采用P控制 →系统稳定性↓ School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fal12015 频域分析-PD控制 G(s)= U=K。+Ts G(s) U(s) G(s) E(s) o) H(s) G.(jo)=K,(1+ Kp L(o)↑ +20 L.(@)=20lgK。+20lgV1+To2 201gk 0 .(@)arctan(T@) p(o)4 +90° +45 K School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 6
2015/12/1 6 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 ( ) ( ) ( ) c P U s G s K E s Lc Kp () 20lg c () 0 Kp>1 开环增益 稳态误差 ωc 过渡过程时间 系统稳定性 原系统稳定裕量充分大时才采用P控制 频域分析--P控制 School of Mechanical Engineering Shanghai Jiao Tong University BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) ( ) ( ) c p d U s G s K T s E s ( ) (1 ) d c p p T G j K j K 2 2 Lc () 20lg Kp 20lg 1Td ( ) arctan( ) c d T 频域分析--PD控制

2015/12/1 频域分析-PD控制(续) 。=) L(4 已校正 校正装置 稳态性能不变 -20 相位裕量个 →稳定性个: K./Ta @ -60 未棱正 a.个→快速性个: 90° 校正法置 0 高频段增益个→抗干扰↓ 90e 己校正 -180 y(o) .270° 未校正 School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 频域分析-PI控制 G(s)= U(s)=Kp+Ts 1 K Ts+1 C() E(s) Ts G(s) Ts H(s) ao-票 L() L(@)=201gK,+201g1+To-20gTo +20 (@)arctan(T)-90 0 积分环节→稳态精度个 q(0)4 0° 岛=方 →稳定性↓ 开环零点 →稳定性↑ -450 -90 School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 7
2015/12/1 7 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 相位裕量 稳定性; c 快速性; 稳态性能不变 高频段增益 抗干扰 (Kp=1) 频域分析--PD控制(续) BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) 1 ( ) ( ) c p i U s G s K E s T s 1 p i i K T s Ts 1 ( ) i c p i jT G j K jT 2 2 L K T gT c p i i ( ) 20lg 20lg 1 20 c i ( ) arctan( ) 90 T 积分环节 稳态精度 稳定性 开环零点 稳定性 频域分析--PI控制
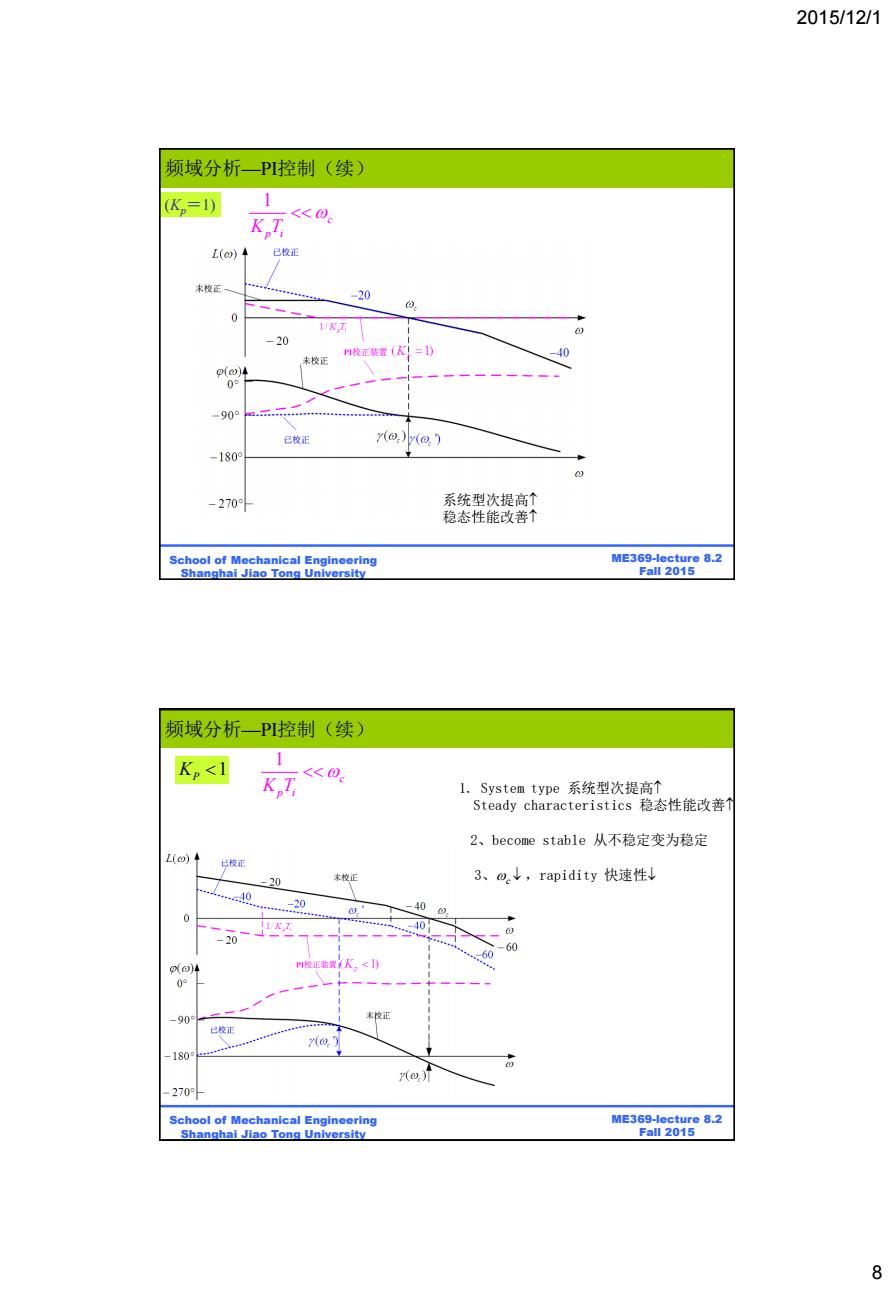
2015/12/1 频域分析PI控制(续) (K2=1) 1 K T <<0 L()◆ 已校正 术校正 20 0 -20 校正装置(K!=1) -40 未校正 p()4 0° 900.mm 已枚正 y(o.)(o.) -180° -270 系统型次提高个 稳态性能改善个 School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 频域分析一PI控制(续) K<1 1 KT <<0 l.System type系统型次提高↑ Steady characteristics稳态性能改善T 2、become stable从不稳定变为稳定 L() 已校正 20 末校正 3、o,↓,rapidity快速性↓ 40 -20 40 40 20 60 -60 o)4 90 校正 已校正 180 ro. 270 School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 8
2015/12/1 8 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 系统型次提高 稳态性能改善 1 c K Tp i (Kp=1) 频域分析—PI控制(续) BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 2、become stable 从不稳定变为稳定 3、c ,rapidity 快速性 KP 1 1 c K Tp i 1. System type 系统型次提高 Steady characteristics 稳态性能改善 频域分析—PI控制(续)
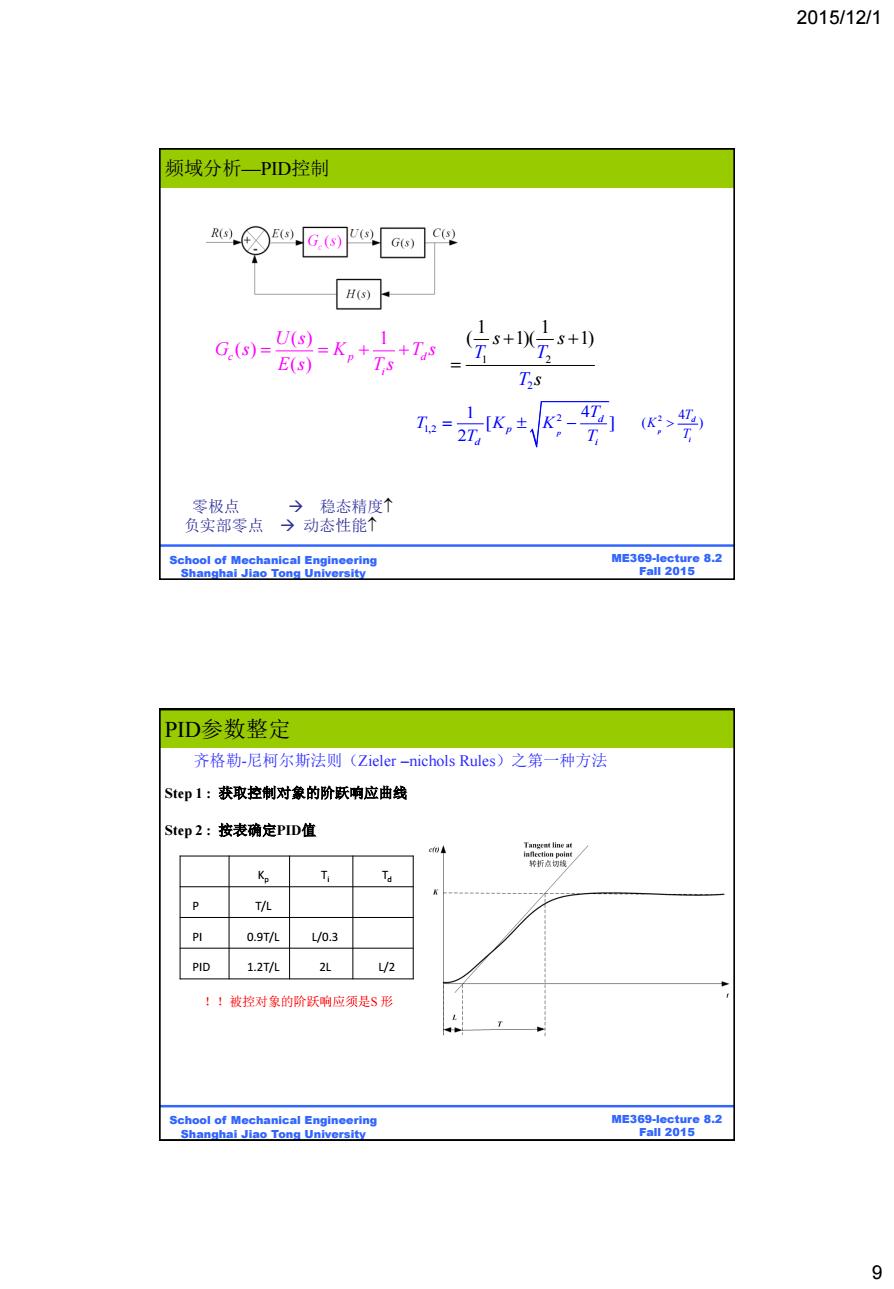
2015/12/1 频域分析PD控制 ☒G.T G(s) H(s) G(s)= U(S=K,+ 1 s+1) +Ts E(s) Ts Ts 1 4T T2= [K,±K (K2> 零极点 →稳态精度个 负实部零点→动态性能个 School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 PID参数整定 齐格勒-尼柯尔斯法则(Zieler-nichols Rules)之第一种方法 Step1:获取控制对象的阶跃响应曲线 Step2:按表确定PID值 Tangeat line at 转折切线 Kp T/L 0.9T/L L/0.3 PID 1.2T/L 2 !!被控对象的阶跃响应须是S形 School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 9
2015/12/1 9 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) 1 ( ) ( ) c p d i U s G s K T s E s T s 2 1,2 1 4 [ ] 2 p d p d i T T K K T T 2 4 ( ) p d i T K T 零极点 稳态精度 负实部零点 动态性能 1 2 2 1 1 ( 1)( 1) T s s T T s 频域分析—PID控制 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University PID参数整定 齐格勒-尼柯尔斯法则(Zieler –nichols Rules)之第一种方法 !!被控对象的阶跃响应须是S 形 Step 1 : 获取控制对象的阶跃响应曲线 Step 2 : 按表确定PID值 Kp Ti Td P T/L PI 0.9T/L L/0.3 PID 1.2T/L 2L L/2

2015/12/1 PID参数整定 齐格勒-尼柯尔斯法则(Zieler-nichols Rules)之第二种方法 Step1:采用P控制,取得使输出第一次呈现持续振荡时的临界增益K,及此时对应的振荡 周期Pr Step2:按表确定PID值 K D Ta 0.5Ka PI 0.45Kr P/1.2 PID 0.6K P/2 P./8 School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 例]PID参数整定 齐格勒-尼柯尔斯法则-2R G.()a C G(s)= s(s+1)(s+5) School of Mechanical Engineering ME369-lecture 8.2 Shanghai Jiao Tong University Fall 2015 10
2015/12/1 10 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University PID参数整定 Step 1 : 采用P控制,取得使输出第一次呈现持续振荡时的临界增益Kcr及此时对应的振荡 周期Pcr Step 2 : 按表确定PID值 Kp Ti Td P 0.5Kcr PI 0.45Kcr Pcr/1.2 PID 0.6Kcr Pcr/2 Pcr/8 齐格勒-尼柯尔斯法则(Zieler –nichols Rules)之第二种方法 BE315-Lecture 8.2 Fall 2011 ME369-lecture 8.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例]PID参数整定 1 ( ) ( 1)( 5) G s s s s 齐格勒-尼柯尔斯法则-2