上海交通大学：《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[07]Lecture53-lineariztion of nonlinear mathematical models 非线性数字模型的线性化

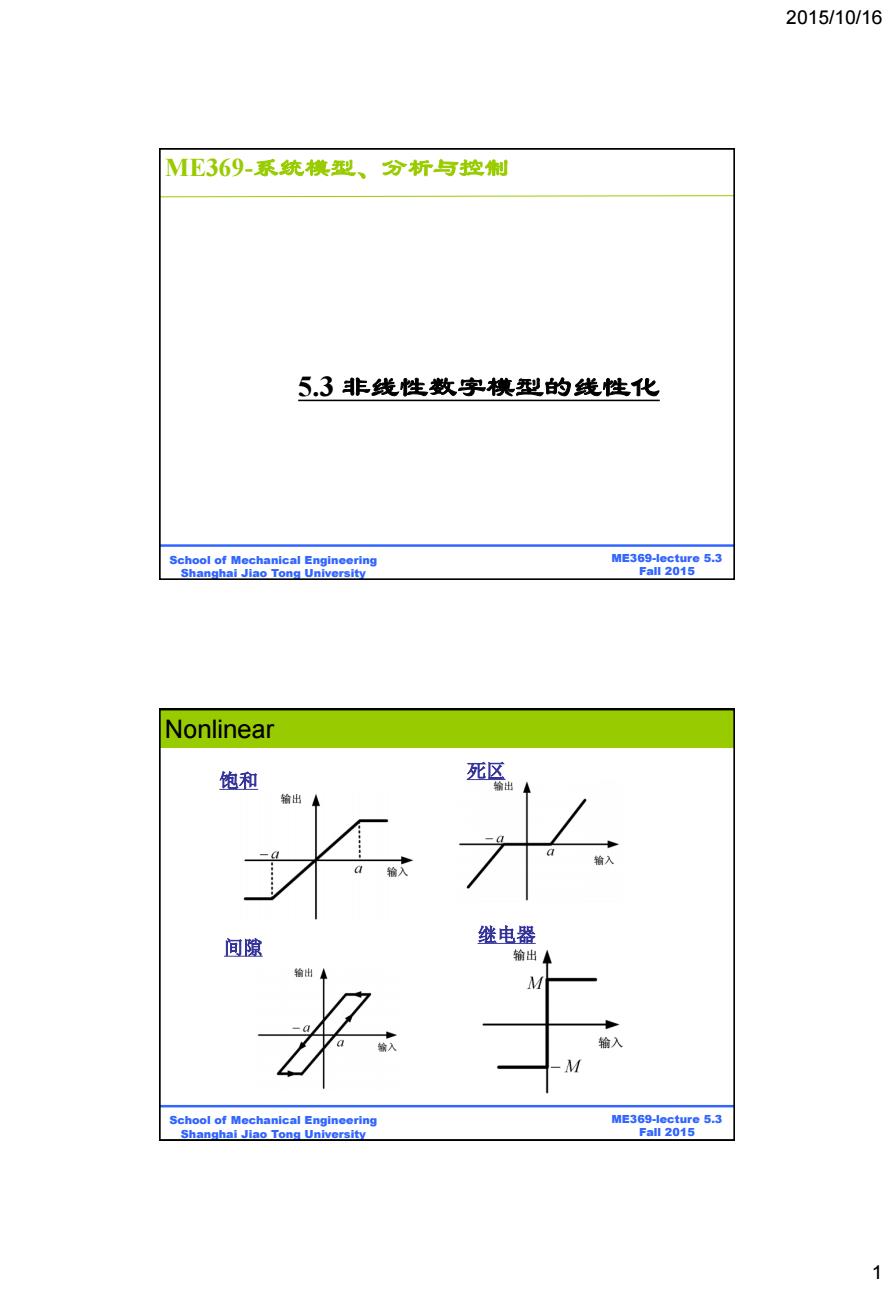
2015/10/16 M369-系统模型、分析与控制 5.3非线性数字模型的线性化 School of Mechanical Engineering ME369-lecture 5.3 Shanghai Jiao Tong University Fall 2015 Nonlinear 饱和 死区 出 输出 a输入 间隙 继电器 输出人 输入 M School of Mechanical Engineering ME369-lecture 5.3 Shanghai Jiao Tong University Fall 2015 1

2015/10/16 1 ME369-lecture 5.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 5.3 非线性数字模型的线性化 ME369-系统模型、分析与控制 ME369-lecture 5.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 饱和 死区 间隙 继电器 Nonlinear

2015/10/16 [例1]单摆 Length Mass m ml+mgsin=0 平衡位置(Equilibrium position)O=0 sin0≈0 很小摆动(Nee swing) mle+mg=0 School of Mechanical Engineering ME369-lecture 5.3 Shanghai Jiao Tong University Fal12015 [例2-1]液位系统 dh o-0 A (横载面积) g.=a√h 取消中间变量Q。 += dt A A School of Mechanical Engineering ME369-lecture 5.3 Shanghai Jiao Tong University Fall 2015 2

2015/10/16 2 ME369-lecture 5.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1]单摆 ml mg     sin 0   0 很小摆动（Wee swing） sin   ml mg     0 平衡位置（Equilibrium position） ME369-lecture 5.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University d 1 d r h a h Q t A A   取消中间变量Qc （横载面积） d d Qr c A h Q t   Q h c  a [例2-1]液位系统

2015/10/16 非线性方程的线性化(Linearization) 忽略 一增量 (徽小偏差) 假设： 在控制系统整个调节过程中，所有变量与稳态值之间只会产生足够微小的偏差。 →增量方程 将参考坐标的原点移到系统或元件的平衡工作点上 School of Mechanical Engineering ME369-lecture 5.3 Shanghai Jiao Tong University Fall 2015 Linearization of single variable function %=f(x) 工作点及静态方程 y=f(x)=f(x)+ (x-x)+7 、,1df 1 df dx 21dr2 x-x)2+…+ -(x-x) n!dx" 泰勒级数展开 保留线性项。略去含有高次的项 =fx=)+(x-x) slope df =K dx dx y=f(x y-=fx)+(x-x)-f) dx df()(x-%) dx △y=△f(x)=K△x 增量方程 School of Mechanical Engineering ME369-lecture 5.3 Shanghai Jiao Tong University Fall 2015 3

2015/10/16 3 ME369-lecture 5.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 非线性方程的线性化（Linearization） ---- 忽略 ----增量 （微小偏差） 假设： 在控制系统整个调节过程中，所有变量与稳态值之间只会产生足够微小的偏差．  增量方程 将参考坐标的原点移到系统或元件的平衡工作点上 ME369-lecture 5.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 0 0 y f x  ( ) 工作点及静态方程 增量方程 保留线性项。略去含有高次的项 0 0 0 d ( ) d ( ) ( ) ( ) f x y f x f x x    x x y f x K x   ( ) 2 (n 0 0 ) 2 2 0 0 d ( ) ( ) ( ) 1 d 1 d ( ) ( ) d 2! d ! d n n f f x x x x x f y f x f x x n x x x           Linearization of single variable function 泰勒级数展开 0 0 0 0 0 0 0 ( ) ( ) d ( ) d d ( ) d ( ) ( ) y y f x x x f x f x f x x x x x        x y f x  ( ) 0 x 0 y 0 x x df slope K dx   

2015/10/16 多变量函数线性化 静态 f(x,y) f(xo2yo) 增量 △fx,)= △f(x,y)=K△x+K△y School of Mechanical Engineering ME369-lecture 5.3 Shanghai Jiao Tong University Fall 2015 [例2-2]液位系统线性化 O School of Mechanical Engineering ME369-lecture 5.3 Shanghai Jiao Tong University Fall 2015 4

2015/10/16 4 ME369-lecture 5.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 0 0 0 0 ( , ) ( , ) ( , ) x y x y f f f x y x y x y          f x y ( , ) 1 2    f x y K x K y ( , )   静态 增量 0 0 f x y ( , ) 多变量函数线性化 ME369-lecture 5.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University d 1 d r h a Q t A h A   [例2-2]液位系统线性化

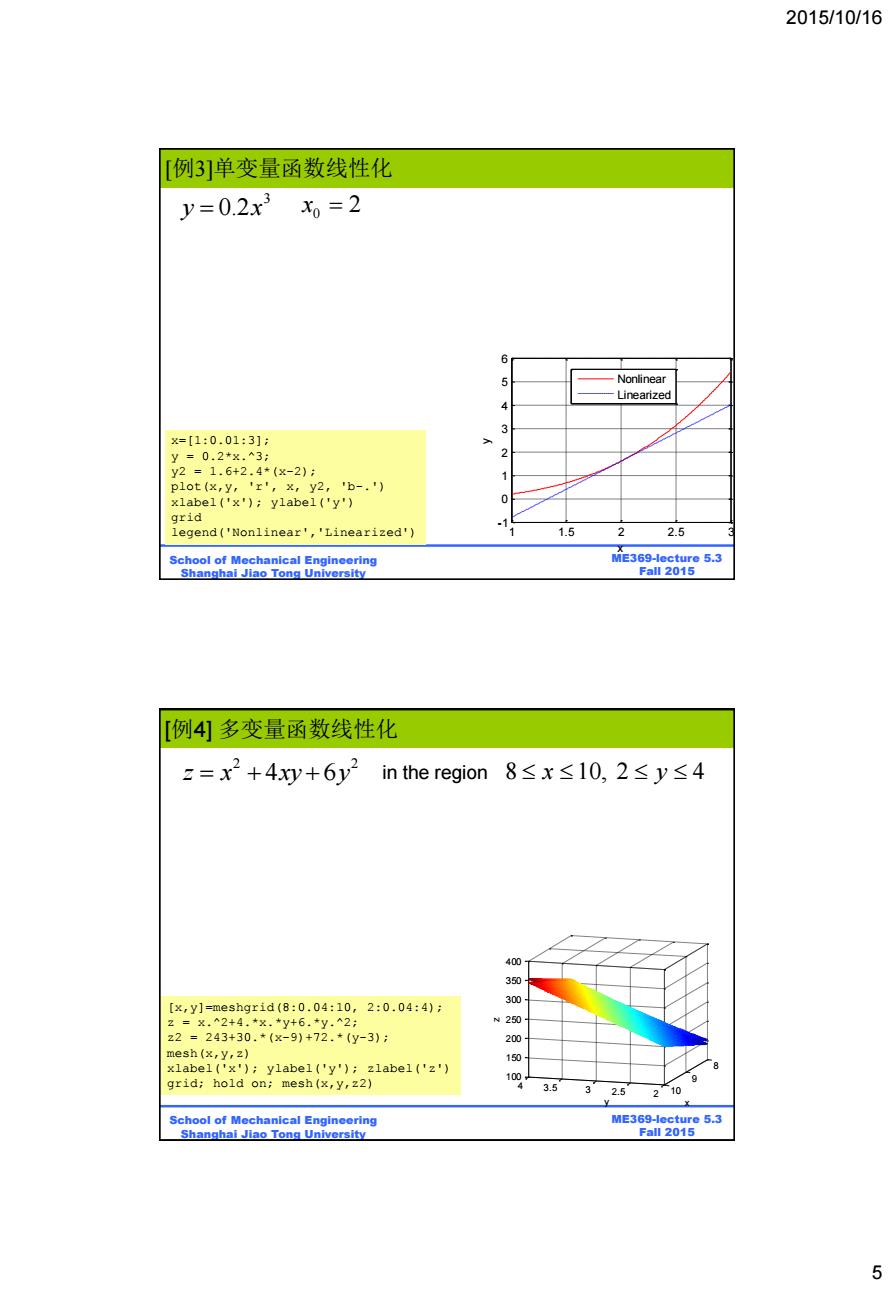
2015/10/16 例3]单变量函数线性化 y=0.2x3 x=2 5 Nonlinear Linearized 4 =[1:0.01:3]: y=0.2*x.3: y2=1.6+2.4*(x-2): 1 plot (x,y,'r',x,y2,'b-.') xlabel('x');ylabel('y') grid legend('Nonlinear','Linearized') 1.5 2 2.5 School of Mechanical Engineering ME369-lecture 5.3 Shanghai Jiao Tong University Fall 2015 [例4]多变量函数线性化 z=x2+4y+6y2 in the region8≤x≤10,2≤y≤4 400 350 [x,y]=meshgrid(8:0.04:10, 2:0.04:4): z=.^2+4.*x.*y+6.*y.^2; N 250 z2=243+30.*(x-9)+72.*(y-3): mesh (x,y,z) 150 xlabel('x');ylabel('y');zlabel('z') grid;hold on;mesh(x,y,z2) 100 3.5 3 2.5 210 School of Mechanical Engineering ME369-lecture 5.3 Shanghai Jiao Tong University Fall 2015 5

2015/10/16 5 ME369-lecture 5.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 3 y x  0.2 0 x  2 1 1.5 2 2.5 3 -1 0 1 2 3 4 5 6 x y Nonlinear Linearized [例3]单变量函数线性化 x=[1:0.01:3]; y = 0.2*x.^3; y2 = 1.6+2.4*(x-2); plot(x,y, 'r', x, y2, 'b-.') xlabel('x'); ylabel('y') grid legend('Nonlinear','Linearized') ME369-lecture 5.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例4] 多变量函数线性化 2 2 z x xy y    4 6 in the region 8 10, 2 4     x y [x,y]=meshgrid(8:0.04:10, 2:0.04:4); z = x.^2+4.*x.*y+6.*y.^2; z2 = 243+30.*(x-9)+72.*(y-3); mesh(x,y,z) xlabel('x'); ylabel('y'); zlabel('z') grid; hold on; mesh(x,y,z2) 8 9 10 2.5 2 3.5 3 4 100 150 200 250 300 350 400 y x z