上海交通大学：《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[15]Lecture81-control system design introduction 控制系统设计概述

ME369-系统模型、分析与控制 8.1控制系统设计概述 School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fall 2015 “控制系统设计”？ 控制系统组成元件 0)控制对象 1)执行元件 2)测量元件 3)给定元件 4)放大元件 设定性能 5)比较元件 6)控制器 7)校正元件（补偿器） School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fall 2015 1

1 ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 8.1 控制系统设计概述 ME369-系统模型、分析与控制 ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University “控制系统设计”？ 控制系统组成元件 0）控制对象 1）执行元件 2) 测量元件 3) 给定元件 4）放大元件 5) 比较元件 6) 控制器 7) 校正元件（补偿器） 设定性能

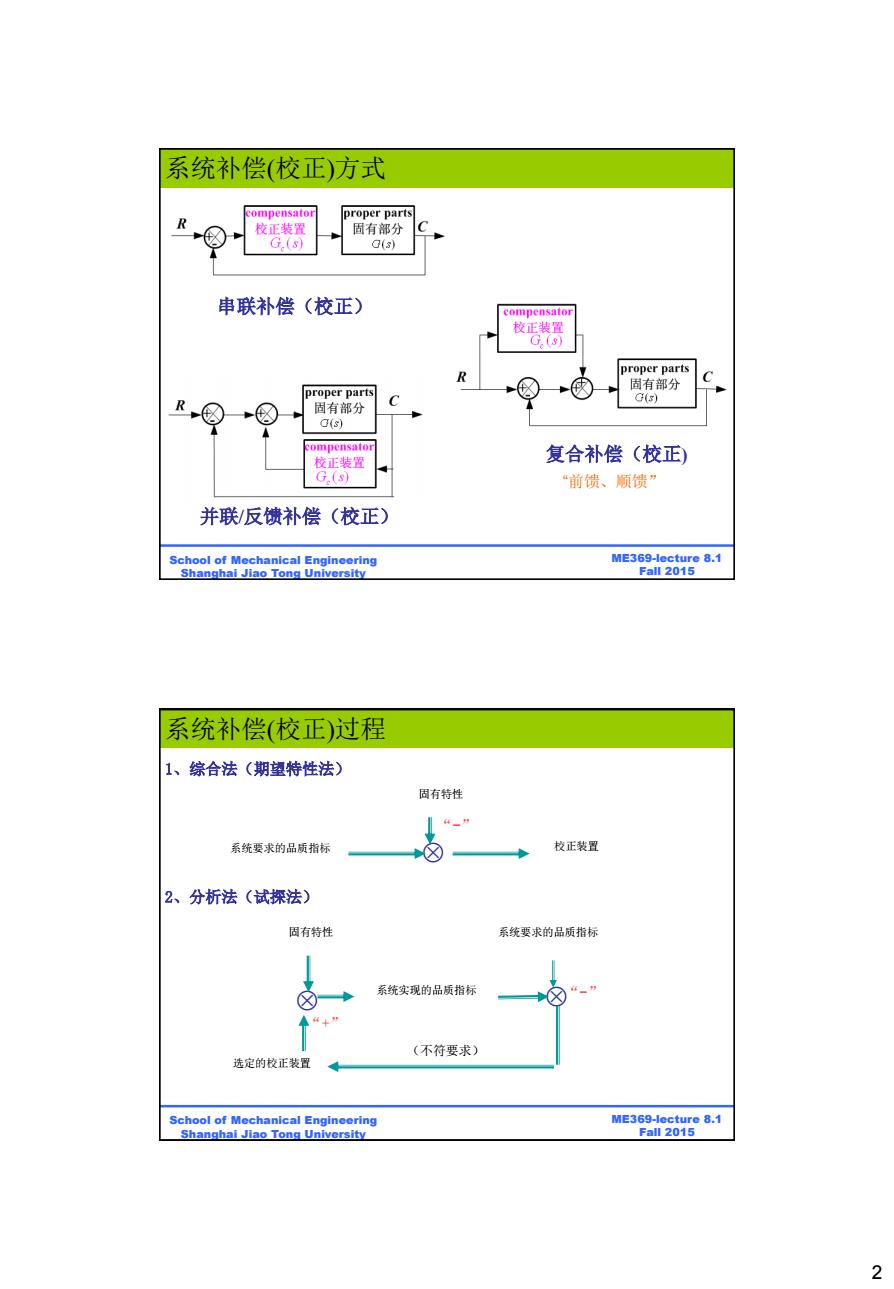
系统补偿（校正）方式 R compensator proper parts +⑧ 校正装置 固有部分 G.(s) (s) 串联补偿（校正） compensator 校正装置 G(3) proper parts +⑧ 固有部分 proper parts C G() R,☒ 固有部分 C(s) compensator 校正装置 复合补偿（校正） G.(8) “前馈、顺馈” 并联/反馈补偿（校正） School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fal12015 系统补偿（校正）过程 1、综合法（期望特性法） 固有特性 系统要求的品质指标 ☒ 校正装置 2、分析法（试探法） 固有特性 系统要求的品质指标 系统实现的品质指标 4+” (不符要求) 选定的校正装置 School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fall 2015 2

2 ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 串联补偿（校正） 并联/反馈补偿（校正） 复合补偿（校正) 系统补偿(校正)方式 “前馈、顺馈” ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 系统补偿(校正)过程 1、综合法（期望特性法） 固有特性 系统要求的品质指标 校正装置  “-” 2、分析法（试探法） （不符要求）   “+” “-” 固有特性 系统要求的品质指标 选定的校正装置 系统实现的品质指标

!?！频率响应设计法 1、频率特性图可以清楚表明系统改变性能指标的方向 2、频域设计通过Bode图进行，处理起来十分简单。 3、对于某些数学模型推导起来比较困难的元件，如液压和气动元件， 通常可以通过频率响应实验来获得其Bode图 4、在涉及到高频噪声时，频域法设计比其他方法更为方便 School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fal12015 三频段 L(@) -20dB/dec -40dB/dec -20dB/dec 03 @ 40dB/dec -60dB/dec 低颜段(《)，) →稳态性能 →大斜率 中麵段(w1~10m,) →动态性能 →斜率一20dB, 足够的带宽 高颜段(>10w.) →抗干扰 →大斜率 School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fall 2015 3

3 ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1、频率特性图可以清楚表明系统改变性能指标的方向 2、频域设计通过Bode图进行,处理起来十分简单。 4、在涉及到高频噪声时，频域法设计比其他方法更为方便 ！？！频率响应设计法 3、对于某些数学模型推导起来比较困难的元件，如液压和气动元件， 通常可以通过频率响应实验来获得其Bode图 ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 低频段 (10ωc ) 抗干扰 斜率 －20dB, 足够的带宽 大斜率 大斜率 三频段

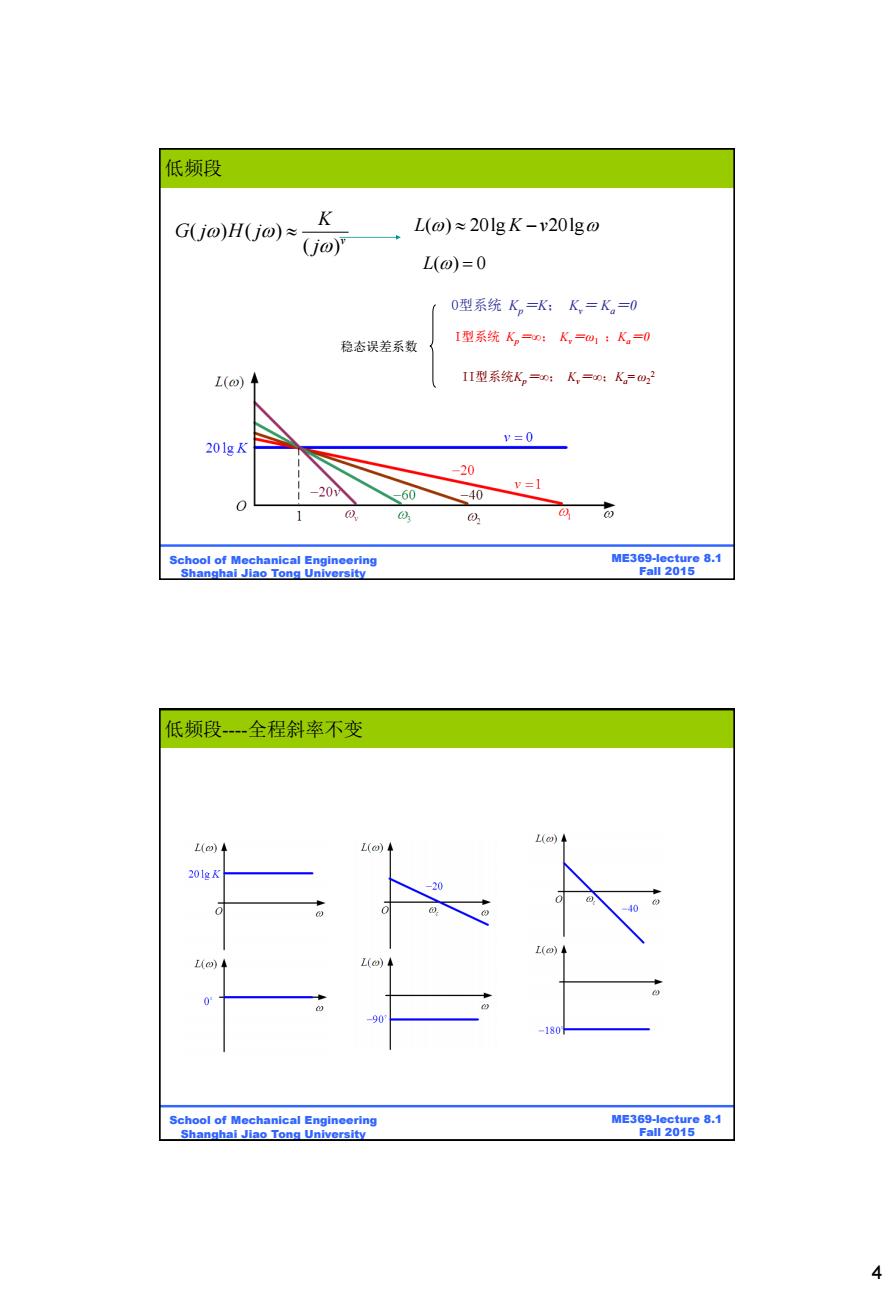
低频段 K Gjo)H(jo)≈ L(o)≈20lgK-v20lgo (jo) L(o)=0 0型系统K。=K:K,=K。=0 稳态误差系数 I型系统K,=0:K,=1:K=0 L(o)◆ I型系统K。=0:K,=0:K。=2 y=0 201gK -20 -20N v=1 60 -40 O 1 0 可 School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fall 2015 低频段全程斜率不变 L(◆ L()◆ L(o) -20 40 L(a)◆ L()◆ L(o) 0. -180 School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fall 2015 4

4 ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) ( ) ( )v K G j H j j     L K v ( ) 20lg 20lg     L( ) 0   稳态误差系数 0型系统 Kp＝K； Kv＝ Ka＝0 I型系统 Kp＝∞； Kv＝ω1 ；Ka＝0 II型系统Kp＝∞； Kv＝∞；Ka= ω2 2 低频段 ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 低频段----全程斜率不变

低频段--中频段保持-20db/dec L() L(o)◆ K G()H(@)=- 2)f)= 0 1+@ jo -20 0 y=180°-g9 y=90° Lo) ◆ GU)H(j) L(ao)◆ 迎+2+（巴1 K1+巴 60 40 G(io)H(io)= 1 (op (Uj)2 -20 -20 物 9 0 y=g1 y=-90°+g1 1-(@2 School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fal12015 高频段 L(co)◆ G(i@)H(jo)= K R jo L(am)◆ G(j)H(j) j0+2+巴 -20 03 -20 7=90° -60 K 25 L(o)◆ G(j)H(jo)=- jo1+@ y=90°-g 1-@ -20 -40 y=90°-g10=g@ @3 School of Mechanical Engineering ME369-lecture 8.1 Shanghal Jiao Tong University Fall 2015 5

5 ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 1 ( ) ( )     j K G j H j   1 1 180 c tg        γ=90° ( ) ( ) K G j H j j     2 1 ( ) (1 ) ( ) ( )      j j K G j H j   1 1 c tg      2 1 1 3 ( ) ( ) [1 ( ) ] ( ) G j H j j j K j           1 1 2 1 2 90 1 ( ) c c tg             低频段----中频段保持-20db/dec ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University (1 ) ( ) ( ) 2     j j K G j H j   1 1 2 2 90 c c tg tg            [1 ( ) ] ( ) ( ) 2 2 2       j j j K G j H j    1 2 2 2 2 90 1 ( ) c c tg            γ=90° ( ) ( ) K G j H j j     高频段

中频段 L( y=90°-g2+g19-g2-g2 -20dB/dec 3 -40dB/dec -20dB/dec *g4-g1丝>0° 0 0 -40dB/dec -60dB/dee 60 50 广mx(o)=tg1√h-g厉=gh/ 2√万 30 h=@ 20 02 3 0 2 4 68101214161820 0mx=V0203= =0h School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fall 2015 中频段 K G(sH(s)= s(0.2s+1)(0.02s+1) K=40.=3.3/sy=52.6 -20dB/dec K=10 0.=6.2/s y=31.7 -40dB/dec K=30 o=11.6/s y=10.3 -40dB/dec K=60o.=16.5/s y=-1.4 -40dB/dec K=12000=61.3/sy=-46.1 -60dB/dec -60dB/dec 背定不稳定 -40dB/dec 可能稳定，但稳定裕量较小 -20dB/dec 一般稳定，且稳定裕量大 School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fall 2015 6

6 ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 1 1 1 1 2 3 4 1 1 2 3 90 0 c c c c c c tg tg tg tg tg tg                              中频段 3 cmax 2 3 2 h h         h h tg h c tg h tg 2 1 1 ( ) 1 1 1 max          3 2 h    ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University –60dB/dec 肯定不稳定 –40dB/dec 可能稳定，但稳定裕量较小 –20dB/dec 一般稳定，且稳定裕量大 ( ) ( ) (0.2 1)(0.02 1) K G s H s s s s    K  4 3.3/ c   s   52.6 20 / dB dec K 10 6.2/ c   s   31.7 40 / dB dec K  30 11.6/ c   s  10.3 40 / dB dec K  60 16.5/ c   s   1.4 40 / dB dec K 1200 61.3/ c   s   46.1 60 / dB dec 中频段

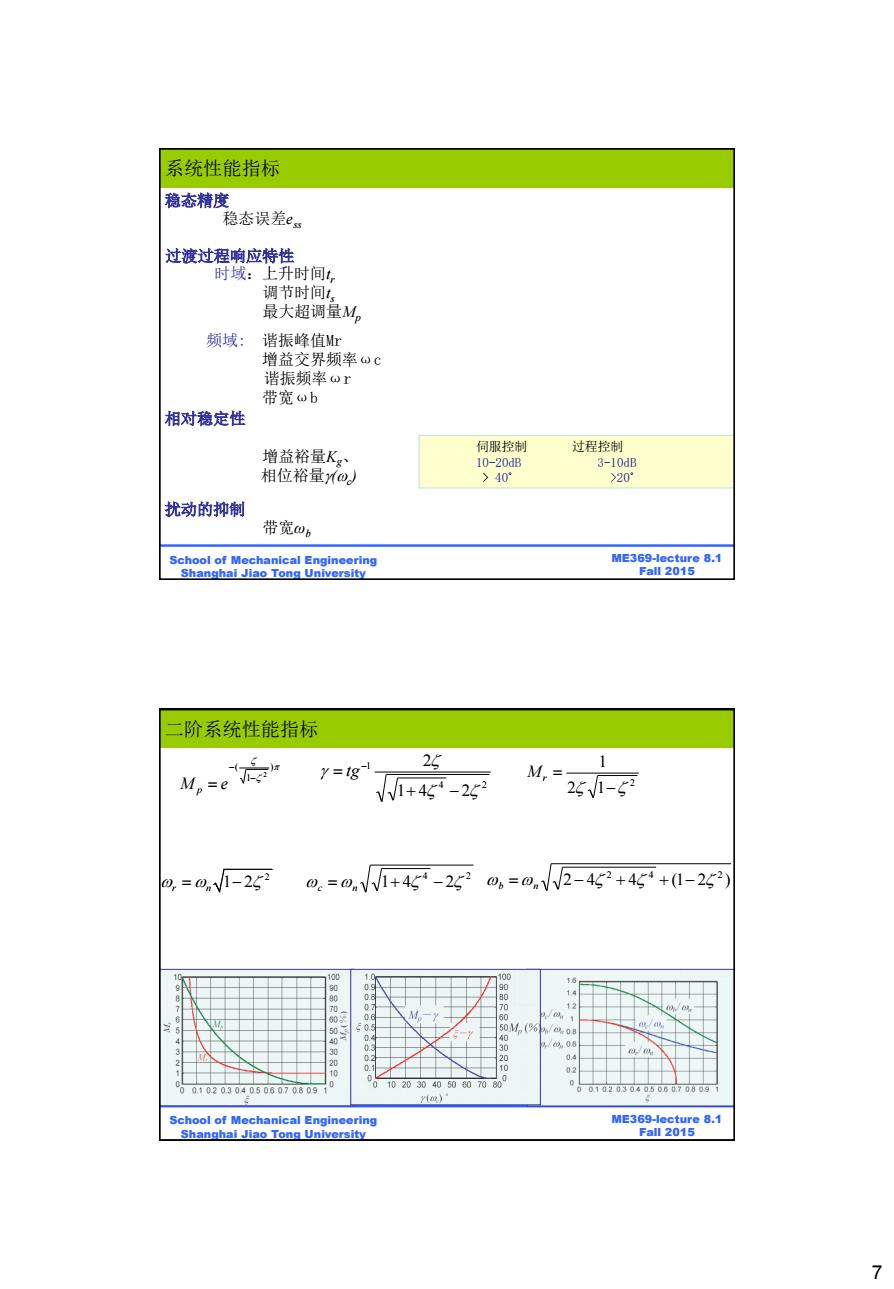
系统性能指标 稳态精 稳态误差e 过渡过程响应特性 时域：上升时间1， 调节时间：， 最大超调量M。 频域：谐振峰值Mr 增益交界频率ωc 谐振频率ωr 带宽wb 相对稳定性 增益裕量Kg、 同服控制 过程控制 10-20dB 3-10dB 相位裕量@。 >40° >20° 扰动的抑制 带宽6 School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fal12015 阶系统性能指标 se 1 Y=18- 25 M, VV1+45-252 25V-5 0,=0V1-252 a.=.V1+45-2520,=0.VV2-42+45+1-252 96000 Mn(% 0.8 02010 03 1020304050070 00102030405060.70.809.1 10203040506070809 r(m)' School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fall 2015 7

7 ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 稳态精度 稳态误差ess 过渡过程响应特性 时域：上升时间t r 调节时间t s 最大超调量Mp 频域: 谐振峰值Mr 增益交界频率ωc 谐振频率ωr 带宽ωb 相对稳定性 增益裕量Kg、 相位裕量(c ) 扰动的抑制 带宽ωb 系统性能指标 伺服控制 过程控制 10-20dB 3-10dB > 40˚ >20˚ ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University    ) 1 ( 2   M  e p 2 2 1 1   Mr  4 2 1 1 4 2 2         tg 二阶系统性能指标 4 2 c n 1 4  2 2    r n  1 2 2 4 4 (1 2 ) 2 4 2 b n       

阶系统性能指标 =±5% 3 1,=- o 04= 31-25 5 3/V2-452+45+0-25) 01= 3N1+4-252 6 5 tgy(o.】 School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fal12015 高阶系统性能指标 高阶系统 主导极点 阶或二阶系统 M。=0.16+0.4M,-1) 1≤M,≤1.8) 经验公式 M,≈ 1 siny (34°≤y≤90) t=- 2+1.5M,-10+2.5M,-12] 0。 School of Mechanical Engineering ME369-lecture 8.1 Shanghai Jiao Tong University Fall 2015 8

8 ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [ ( )] 3 1 4 2 6 4 2 c c s tg t              2 3 1 2 r t s       3 2 4 4 (1 2 ) 2 4 2     b t s  3 s n t     5% 二阶系统性能指标 ME369-lecture 8.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 经验公式  0.16 0.4( 1) M p Mr (1 1.8)   Mr sin 1 Mr  (34 90 )      [2 1.5( 1) 2.5( 1) ] 2   r   r  c t s M M   高阶系统 一阶或二阶系统 高阶系统性能指标 主导极点