上海交通大学：《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[13]Lecture73-stability analysis in frequency domain 系统稳定性的频域分析

ME369-系统模型、分析与控制 7.3系统稳定性的频域分析 School of Mechanical Engineering ME369-lecture 7.3 Shanghai Jiao Tong University Fall 2015 特征矢量与稳定性 一阶系统 s平面 D(s)=s+p D)=1+ 0 (s=j0) s平面 s平面 D(jo) D(jo jo D(j0) ∠DU -P -P -D 【正实特征根】 【负实特征根】 4∠Djo)=T 4∠Djo)=- 0++o 2 r-0◆+o 2 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 1

1 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering ME369-lecture 7.3 Shanghai Jiao Tong University 7.3 系统稳定性的频域分析 ME369-系统模型、分析与控制 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 特征矢量与稳定性 一阶系统 D s s p ( )   【负实特征根】 【正实特征根】 :0 ( )  2       D j : 0 ( )  2         D j （s j  ）

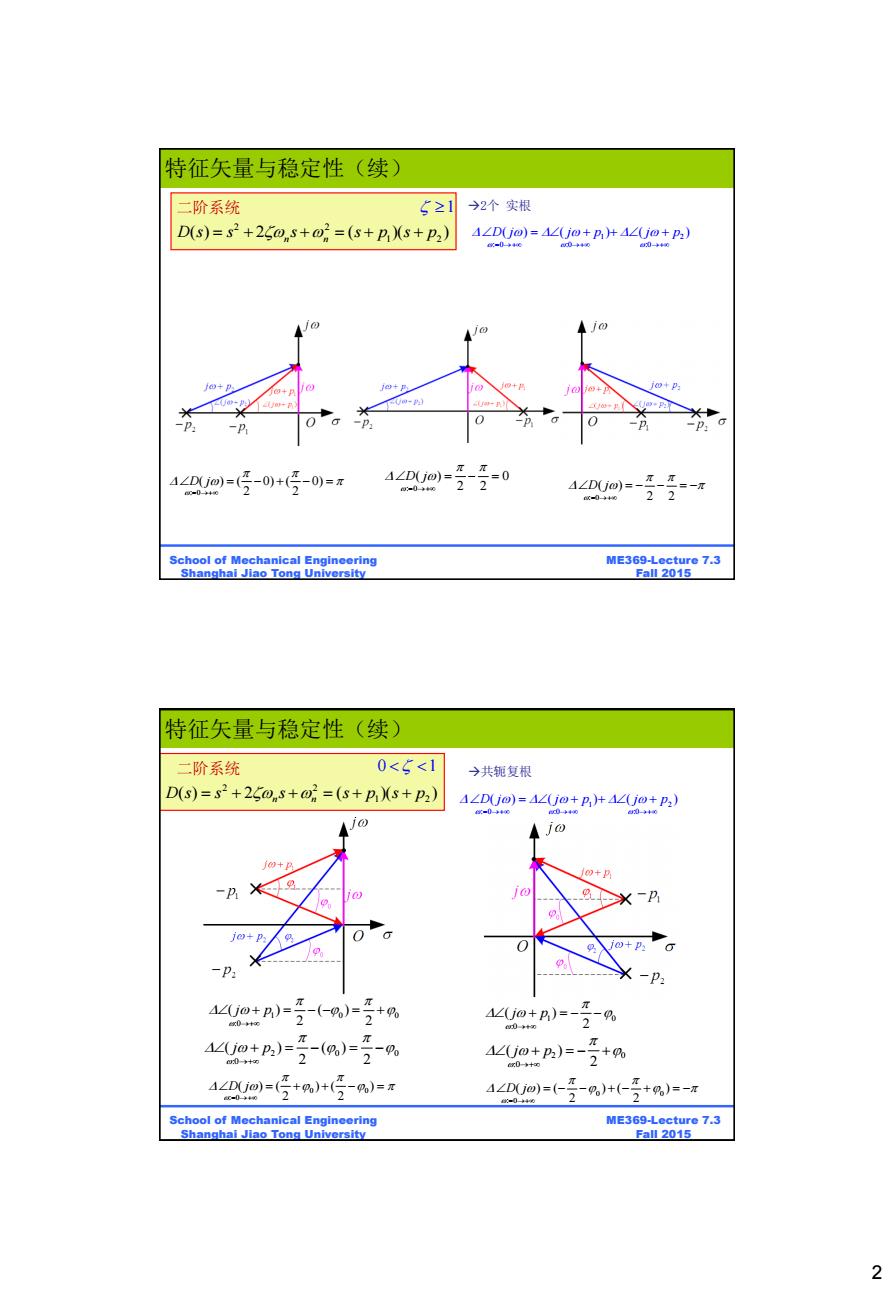
特征矢量与稳定性（续） 二阶系统 521 →2个实根 D(s)=s2+25D,S+o2=(s+Ps+P2) 4∠Djo)=4jo+BHA∠(Uo+P) -0→4 0 jo @+P +P + 1+ -P: ππ 4∠DU)=( -0)+ 2 -0)=π A∠DUj)= -0+e 4∠D(jo)=- =一π 22 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 特征矢量与稳定性（续） 二阶系统 0<5<1 →共轭复根 D(s)=s2+25@s+=(s+pXs+P2) 4∠DUjo)=4∠Uo+B+4∠(jo+P2) =040 040 'u040 j + 10+p -P x-p g入J+P P. X-P 4∠(jo+B)= (%)= π +% A∠j0+乃)=- 0+ 0+汤 2% 4(o+B)= (%) 2 2% 4Uo+Pp2)= 0十0. 2+% A∠Dj=( c-00 +)+（区 2 %)=π =0440 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 2

2 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 二阶系统 2 2 1 2 ( ) 2 ( )( ) D s s s s p s p n n          1 : 0 ( ) ( 0) ( 0) 2 2 D j               : 0 ( ) 0 2 2 D j            : 0 ( ) 2 2 D j               2个 实根 1 2 : 0 :0 :0 D j j p j p ( ) ( ) ( )                     特征矢量与稳定性（续） ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 0 1    1 0 0 :0 ( ) ( ) 2 2 j p                2 0 0 :0 ( ) ( ) 2 2 j p               0 0 : 0 ( ) ( ) ( ) 2 2 D j                 1 0 :0 ( ) 2 j p            2 0 :0 ( ) 2 j p           0 0 : 0 ( ) ( ) ( ) 2 2 D j                    共轭复根 1 2 : 0 :0 :0 D j j p j p ( ) ( ) ( )                     2 2 1 2 ( ) 2 ( )( ) D s s s s p s p n n         特征矢量与稳定性（续） 二阶系统

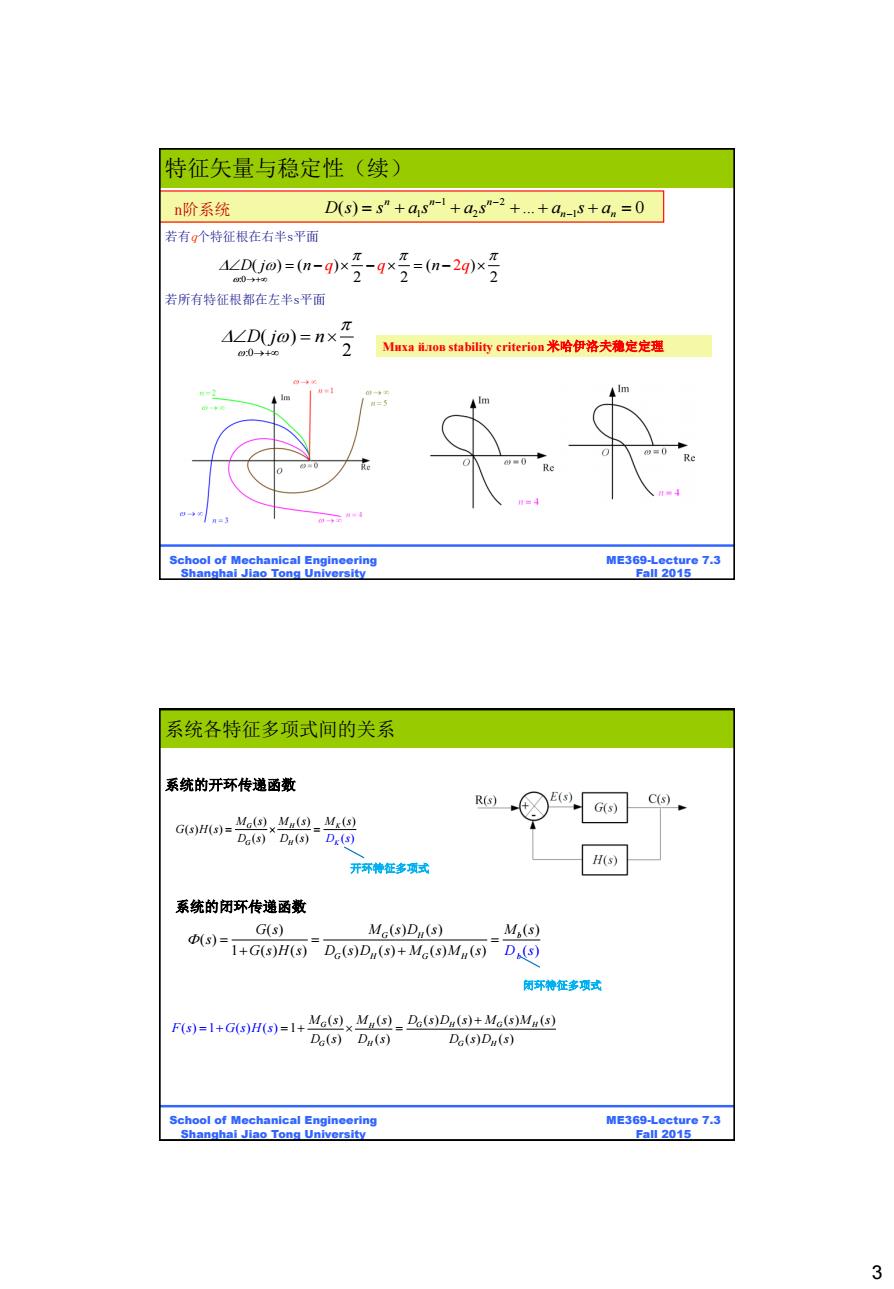
特征矢量与稳定性（续） n阶系统 Ds）=3”+a3-+as"-2++an-3+an=0 若有g个特征根在右半s平面 A/D(jo)=(n-q)xI 0→+a0 =a-240x号 若所有特征根都在左半s平面 ALD(j0)=nX2 00-→+0 Mmxa蓝ostability criterion米哈伊洛夫稳定定理 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 系统各特征多项式间的关系 系统的开环传递函数 R(s) E(s) G(s) C(s) Gs)H(s）= Ma(s)Mu(s)M(s) Da(s)Du(s)De(s) 开环神征多项式 H(s) 系统的闭环传递函数 (s)= G(s) MG(s)Du(s) M,(s) 1+G(s)H(s)Da(s)Du(s)+MG(s)Mn(s)D(s) 闭环神征多项式 Fs=l+GsH句=l+Me(xMn@_Ds)DaS)+Me(s)M包 D(s)D(s) Da(s)Da(s) School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 3

3 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 若所有特征根都在左半s平面 若有q个特征根在右半s平面 :0 ( ) ( ) ( ) 2 2 2 D j n q q n 2q                 :0 ( ) 2 D j n        ( ) ... 1 0 2 2 1   1         n n n n n n阶系统 D s s a s a s a s a Миха йлов stability criterion 米哈伊洛夫稳定定理 特征矢量与稳定性（续） ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 闭环特征多项式 系统的开环传递函数 系统的闭环传递函数 ( ) ( ) ( ) ( ) ( ( ) ) ( ) ( ) G H K G H K M s M s M s G s H s D s D s D s    ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ) ) ( ( ) G H b G H G H b G s M s D s M s s G s H s D s M M s D s s D s       ( ) ( ) ( ) ( ( ) 1 ( ) ) ( ) 1 ( ) ( ) ( ) ( ( ) ( ) ) G G H G H H G H G H M s D s D s M s M s M s D s D s D s D s F s G s H s        系统各特征多项式间的关系 开环特征多项式

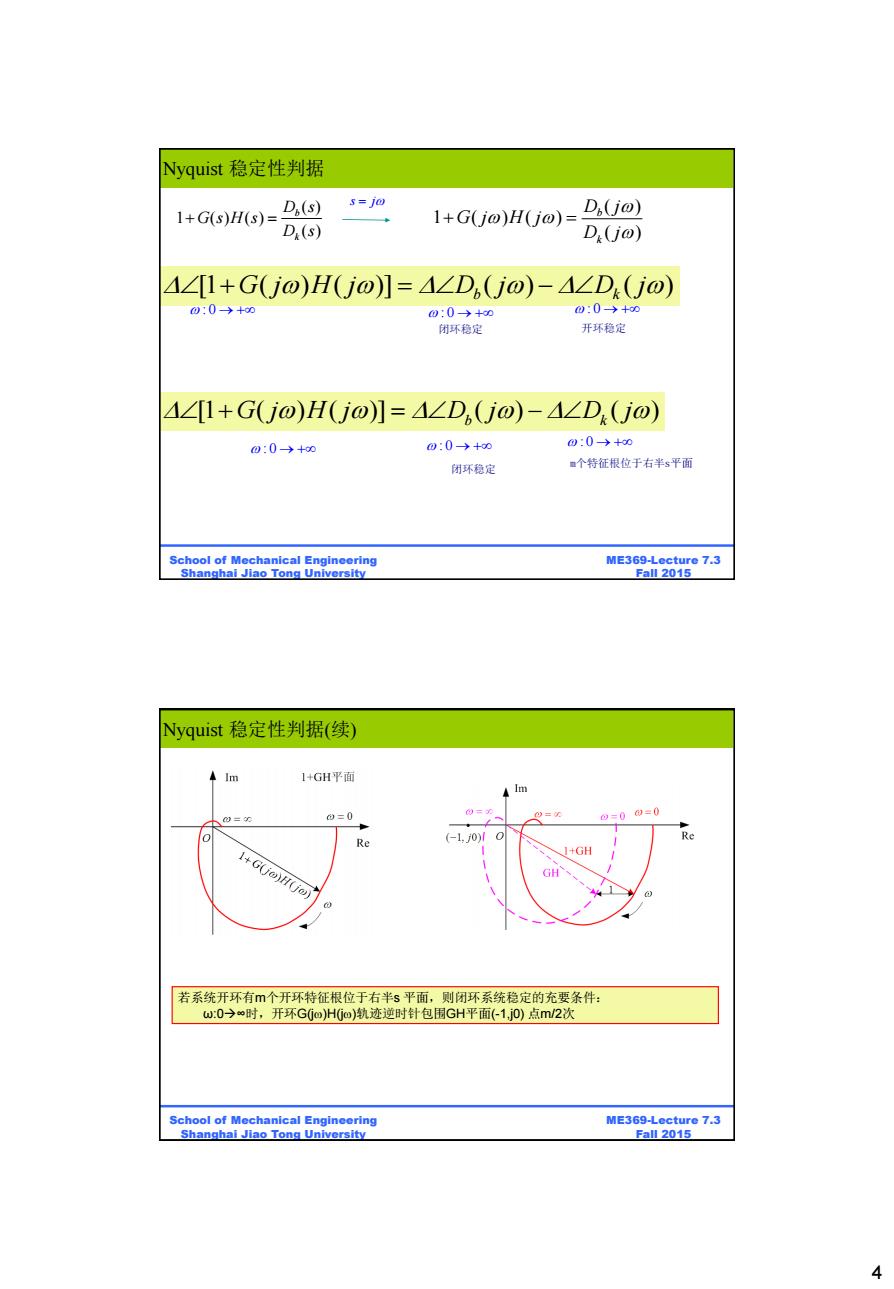
Nyquist稳定性判据 D,(s) 3=j0 1+G(s)H(s)= 1+G(jo)H(U@)= D,(jo) D(s) D(jo) A∠1+G(jo)H(jo)]=4∠D(jo)-A∠D(jo) 0:0→+0 0:0→+0 0:0→+0 闭环稳定 开环稳定 4∠1+G(jo)H(jo)]=△∠D,(jo)-4∠D(Uo) 0:0→+0 0:0→+0 0:0→+0 闭环稳定 ■个特征根位于右半s平面 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 Nyquist稳定性判据（续） ◆lm 1+GH平面 A Im 0=0 =0 ”= =001=0 Re Re 1+GH 1+G(jo GH 若系统开环有m个开环特征根位于右半s平面，则闭环系统稳定的充要条件： w:0→∞时，开环G(o)Ho)轨迹逆时针包围GH平面(-1，j0)点m/2次 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 4

4 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [1 ( ) ( )] ( ) ( )              G j H j D j D j b k ( ) ( ) 1 ( ) ( ) D s D s G s H s k b   ( ) ( ) 1 ( ) ( )     D j D j G j H j k b   闭环稳定 开环稳定 s j    :0   Nyquist 稳定性判据  :0    :0   [1 ( ) ( )] ( ) ( )              G j H j D j D j b k m个特征根位于右半s平面  :0    :0    :0   闭环稳定 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Nyquist 稳定性判据(续) 若系统开环有m个开环特征根位于右半s 平面，则闭环系统稳定的充要条件： ω:0∞时，开环G(j)H(j)轨迹逆时针包围GH平面(-1,j0) 点m/2次

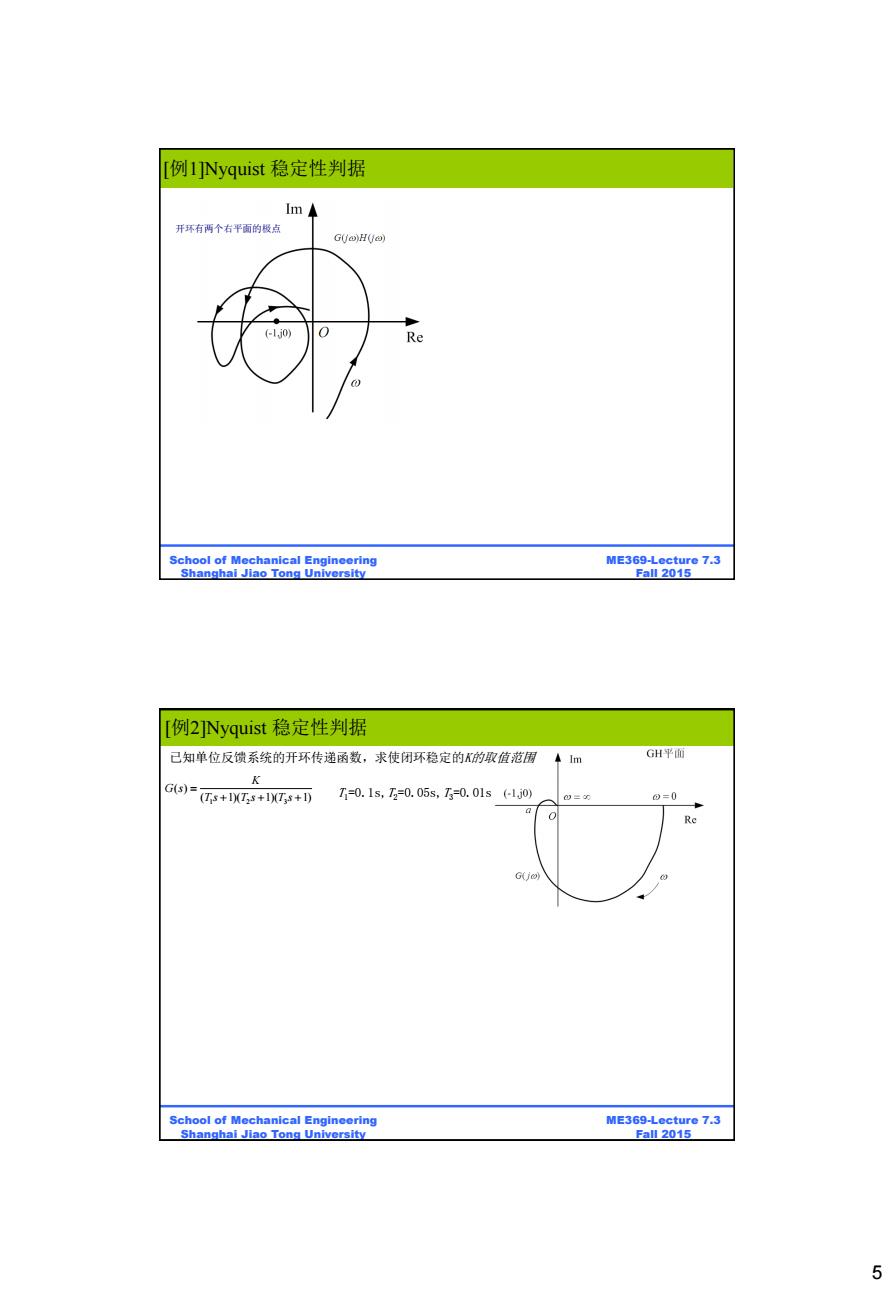
T例1 Nyquist稳定性判据 Im◆ 开环有两个右平面的极点 G(o)H() 10) 0 Re School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 [例2 Nyquist稳定性判据 已知单位反馈系统的开环传递函数，求使闭环稳定的的取值范围 GH平面 G)严p+lXI+T+ T=0.1s,T2=0.05s,T=0.01s1j0) a)=0 0=0 Re G(jw) School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 5

5 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 开环有两个右平面的极点 [例1]Nyquist 稳定性判据 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 2 3 ( ) ( 1)( 1)( 1) K G s T s T s T s     已知单位反馈系统的开环传递函数，求使闭环稳定的K的取值范围 T1=0.1s,T2=0.05s,T3=0.01s [例2]Nyquist 稳定性判据

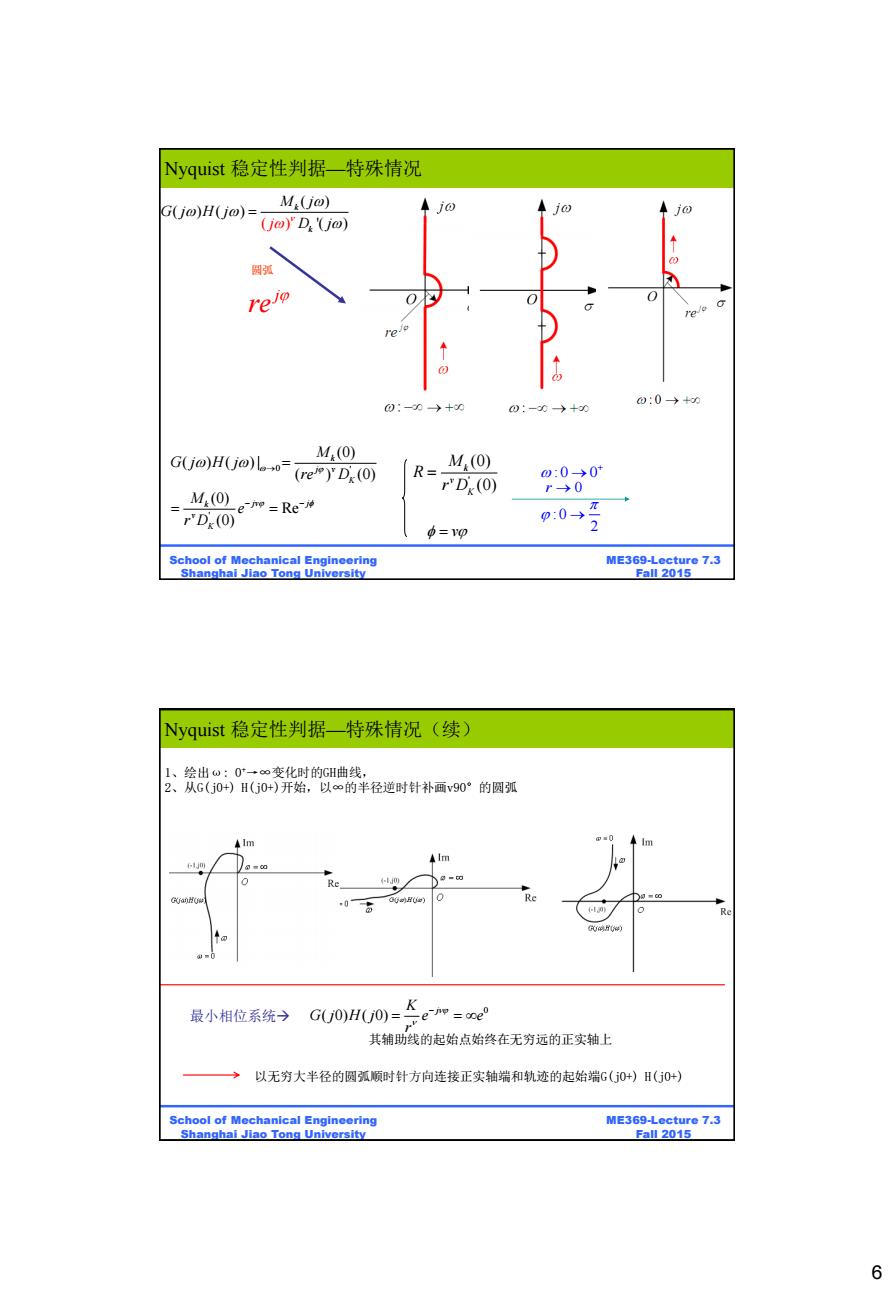
Nyquist稳定性判据特殊情况 G(j@)H(j@)= M(jo) jo Um)'D'(j@) 删弧 Felo 1 e o 0:-0+0 0:0→+0 0:-0→+0 GUo)Hjo)l。-6= M(0) (re)"D(0) R= M(0) 0:00+ r'D(0) M,(O) r→0 m=Re帅 r'D(0) 中=1p 90→2 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 Nyquist稳定性判据特殊情况（续） I、绘出w:0→∞变化时的GH曲线， 2、从G(j0+)H(j0+)开始，以∞的半径逆时针补画v90°的圆弧 lm =0 ◆lm Re 0 a K 最小相位系统) GU0)HG0)=△ep=ne° 其辅助线的起始点始终在无穷远的正实轴上 →以无穷大半径的圆弧顺时针方向连接正实轴端和轨迹的起始端G(j0+)H(0+) School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 6

6 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 圆弧 j re  ( ) ( ) ( ) '( ) ) ( k k M j G j H j j D j        :0 2    0 ' ' (0) ( ) ( ) | ( ) (0) (0) Re (0) k j v K k jv j v K M G j H j re D M e r D             ' (0) (0) k v K M R r D     v :0 0   r  0 Nyquist 稳定性判据—特殊情况 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1、绘出ω: 0+→∞变化时的GH曲线， 2、从G(j0+) H(j0+)开始，以∞的半径逆时针补画v90°的圆弧 最小相位系统 0 ( 0) ( 0) K j G j H j e e r       其辅助线的起始点始终在无穷远的正实轴上 以无穷大半径的圆弧顺时针方向连接正实轴端和轨迹的起始端G(j0+) H(j0+) Nyquist 稳定性判据—特殊情况（续）

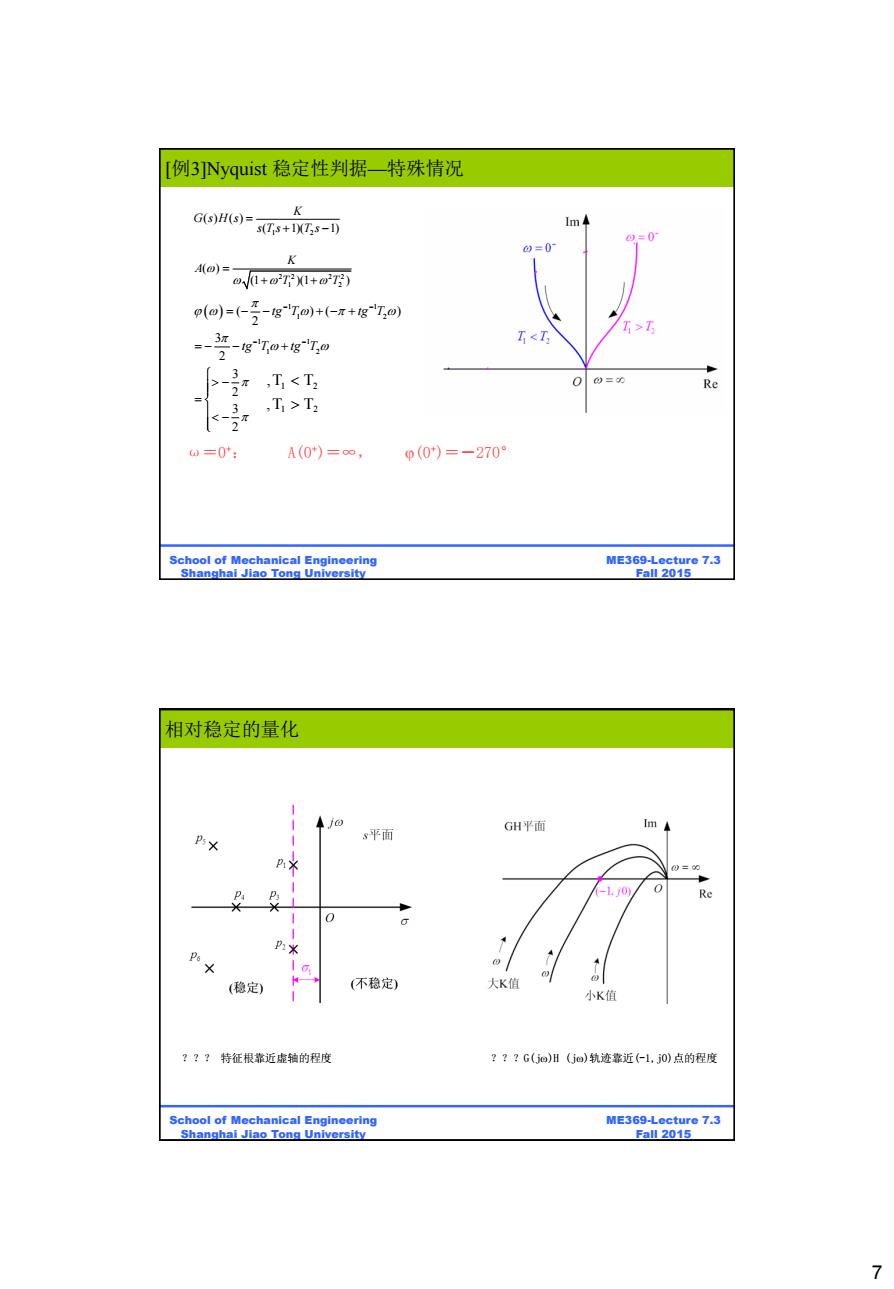
[例3 Nyquist稳定性判据特殊情况 G(s)H(s)= ← s(Ts+IXTs-1) Im4 =0 0=0 40)= o(1+oTX1+@'T) po)=-受g7oj+(-+go） -受-g7a+gTe TT 0=0 Re = 3 ,T1>T2 0=0*: A(0）=∞， 0(0)=-270° School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 相对稳定的量化 GH平面 s平面 B -1,j0 Re 米 + (稳定) (不稳定) 大K值 小K值 ???特征根靠近虚轴的程度 ???G(@)H(jo)轨迹靠近(-1，j0)点的程度 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 7

7 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University   1 1 1 2 1 1 1 2 ( ) ( ) 2 3 2 3 2 3 2 tg T tg T tg T tg T                                  ω＝0 +： A(0+)＝∞， (0+)＝－270° 1 2 ( ) ( ) ( 1)( 1) K G s H s s T s T s    2 2 2 2 1 2 ( ) (1 )(1 ) K A T T        1 2 1 2 ,T T ,T T   [例3]Nyquist 稳定性判据—特殊情况 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ？？？ 特征根靠近虚轴的程度 ？？？G(j)H (j)轨迹靠近(-1,j0)点的程度 相对稳定的量化

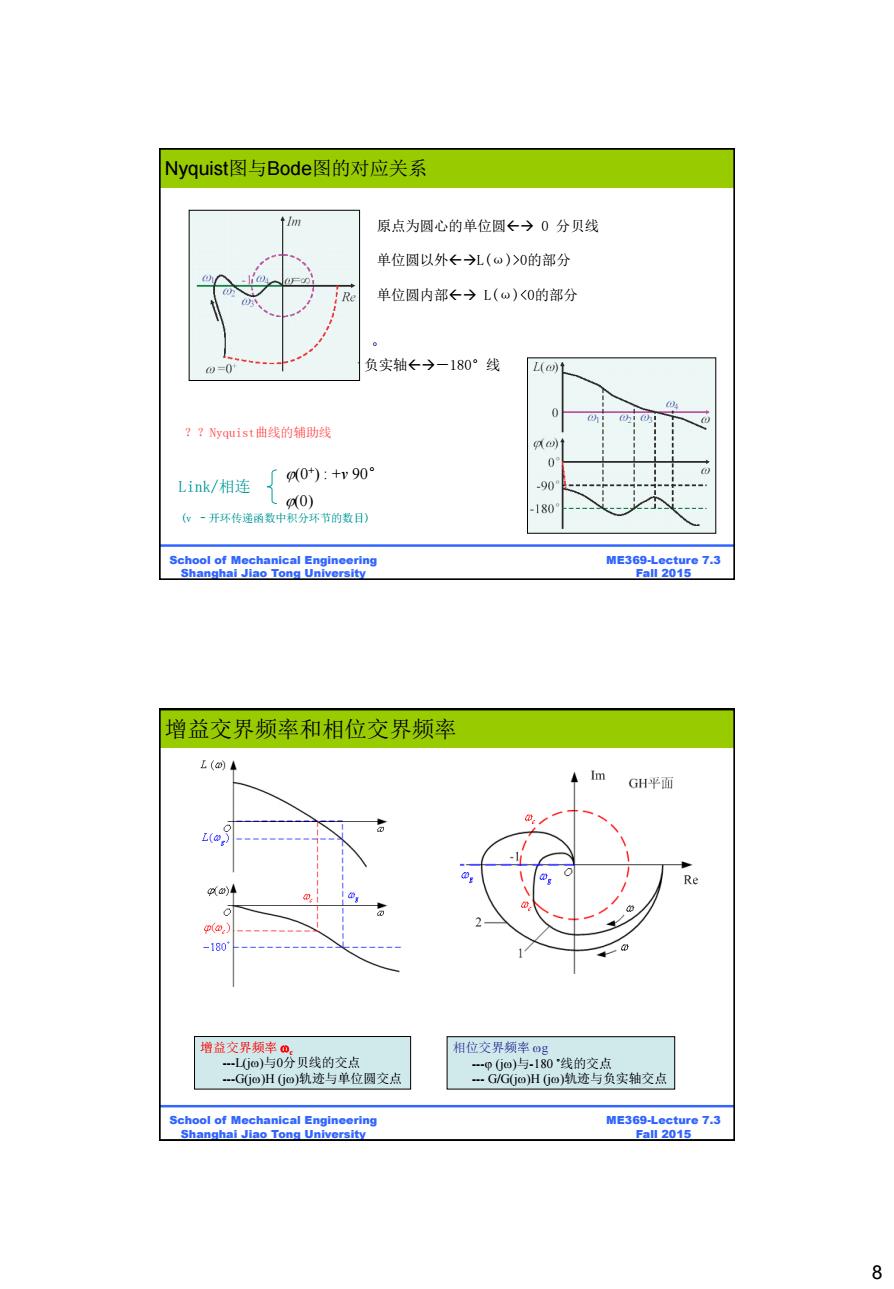
Nyquist图与Bode图的对应关系 ↑lm 原点为圆心的单位圆←→0分贝线 单位圆以外←→L(0)>0的部分 Re 单位圆内部←→L(w)<0的部分 =0 负实轴←→-180°线 L(o ?？Nyquist曲线的辅助线 o) 00*):+v90° 0 Link/相连 90 0) 180 (w一开环传递函数中积分环节的数目) School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 增益交界频率和相位交界频率 L(+ A Im GH平面 Re @)4 4p@ -180 增益交界频率m。 相位交界频率四g -LG回)与0分贝线的交点 -pGo)与-180线的交点 G(oHGo)轨迹与单位圆交点 -…G/GGo)HGo)轨迹与负实轴交点 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 8

8 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 原点为圆心的单位圆 0 分贝线 单位圆以外L(ω)>0的部分 单位圆内部 L(ω)<0的部分 ° 负实轴－180°线 Link/相连 (v –开环传递函数中积分环节的数目) (0) ？？Nyquist曲线的辅助线 (0+ ) : +v 90° Nyquist图与Bode图的对应关系 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 增益交界频率 c ---L(j)与0分贝线的交点 ---G(j)H (j)轨迹与单位圆交点 相位交界频率 g --- (j)与-180 ˚线的交点 --- G/G(j)H (j)轨迹与负实轴交点 增益交界频率和相位交界频率

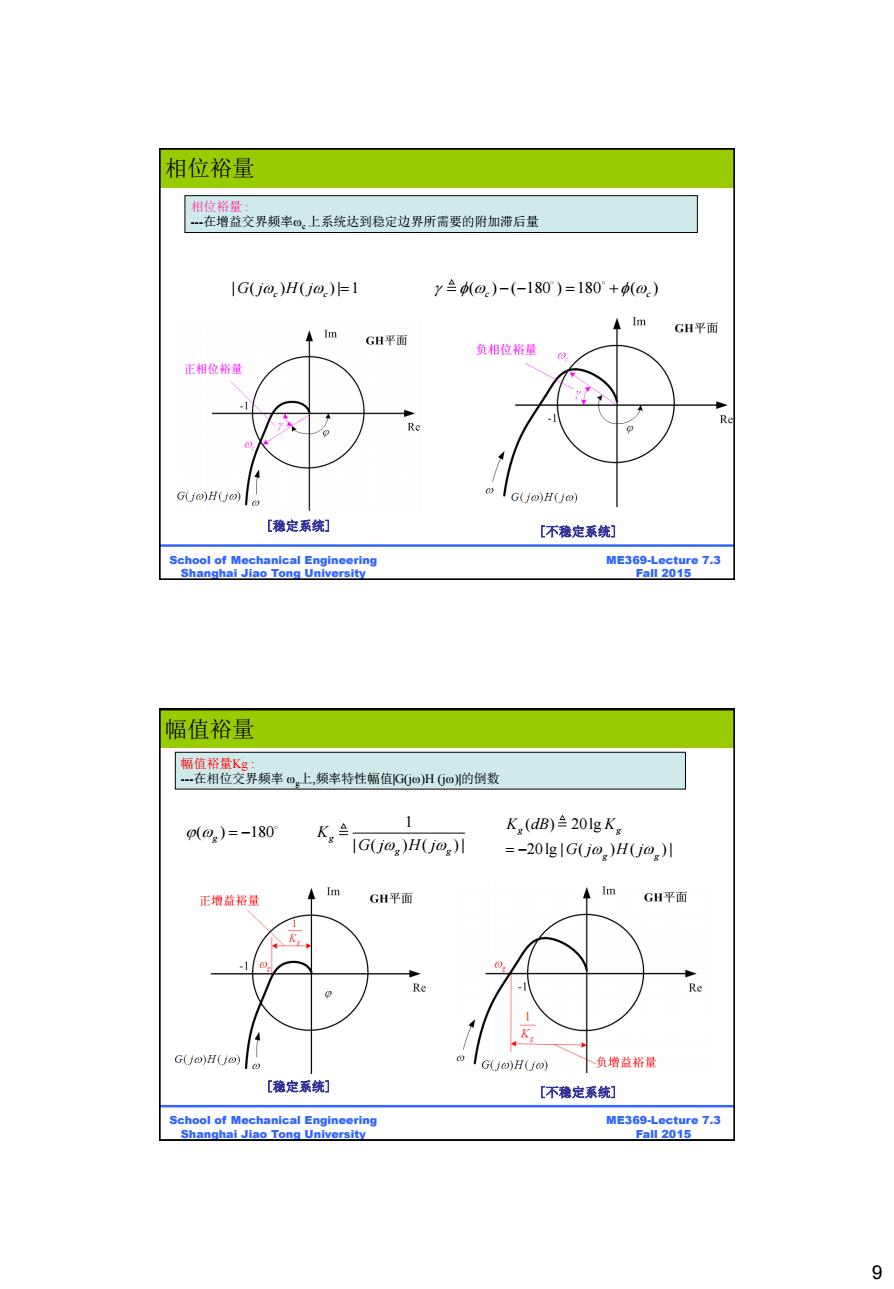
相位裕量 相位裕量 一在增益交界频率0。上系统达到稳定边界所需要的附加滞后量 IG(j@)H(j@.)F1 y兰(@.)-(-180)=180°+@) Im m GH平面 GH平面 负相位裕量 正相位裕量 Re e Gjo)H(j)o I G(j@)H(jo) [稳定系统] [不稳定系统] School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 幅值裕量 幅值裕量Kg: -在相位交界频率o。上，频率特性幅值G(GoH(o)的倒数 p(0)=-180 K(dB)≌20lgKg G(j@)H(j@g) =-20lg1GU0)H(U0)川 Im 正增益裕量 GH平面 A Im GH平面 Re Re G(H(j) G(JH(io) 、负增益裕量 [稳定系统] [不稳定系统] School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 9

9 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University | ( ) ( ) | 1 G j H j   c c  ( ) ( 180 ) 180 ( ) c c          相位裕量 : ---在增益交界频率c 上系统达到稳定边界所需要的附加滞后量 [不稳定系统] [稳定系统] 相位裕量 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 幅值裕量Kg : ---在相位交界频率 g上,频率特性幅值|G(j)H (j)|的倒数 ( ) 180  g   1 | ( ) ( ) | g g g K G j H j   ( ) 20lg 20lg | ( ) ( ) | g g g g K dB K   G j H j   幅值裕量 [不稳定系统] [稳定系统]

[例4]稳定裕量 已知单位反馈系统的开环传递函数，求取稳定裕量 100 Gs)=- +++2+0 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 稳定系统的稳定裕量 G(i@H (i@)轨迹： -一不包围(-1j0)点： -一先穿过单位圆，后穿过负实轴 L(◆ Positive gain margin Positive gain margin ◆Im 正增益裕量 正增益裕量 GH平面 正相位裕量 Positive 心 phase margin Re (4 -180 G(jo)H(jo) 正相位裕量 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 10

10 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 5 100 ( ) ( 2)( 10) ( 1)( 1) 2 10 G s s s s s s s       已知单位反馈系统的开环传递函数，求取稳定裕量 [例4]稳定裕量 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University G(j)H (j)轨迹: ---不包围(-1,j0)点; ---先穿过单位圆，后穿过负实轴 稳定系统的稳定裕量 Positive gain margin Positive gain margin Positive phase margin