上海交通大学：《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[13]Lecture72-frequency characteristic plots 频率特性图

2015/11/14 ME369-系统模型、分析与控制 7.2频率特性图 School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 伯德图/波德图(Bode diagrams)定义 -对数幅频图(Magnitude Plot) L(@)=201g|G(j@)|vs logo@ 对数相频图(Phase Plot) p(o)=∠Gjo)vs log1oo 20 150 decade (dec) 40 一个十倍频程 0 02 04 0.60.8 1 0 10e 0 个 一个十倍颜程 倍频程 倍频程 150 60 octave School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 1

2015/11/14 1 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 7.2 频率特性图 ME369-系统模型、分析与控制 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 伯德图/波德图（Bode diagrams ）定义 decade (dec) L G j ( ) 20lg | ( ) |       ( ) ( )  G j VS 10 log  --对数幅频图(Magnitude Plot ) VS 10 log  --对数相频图(Phase Plot ） octave

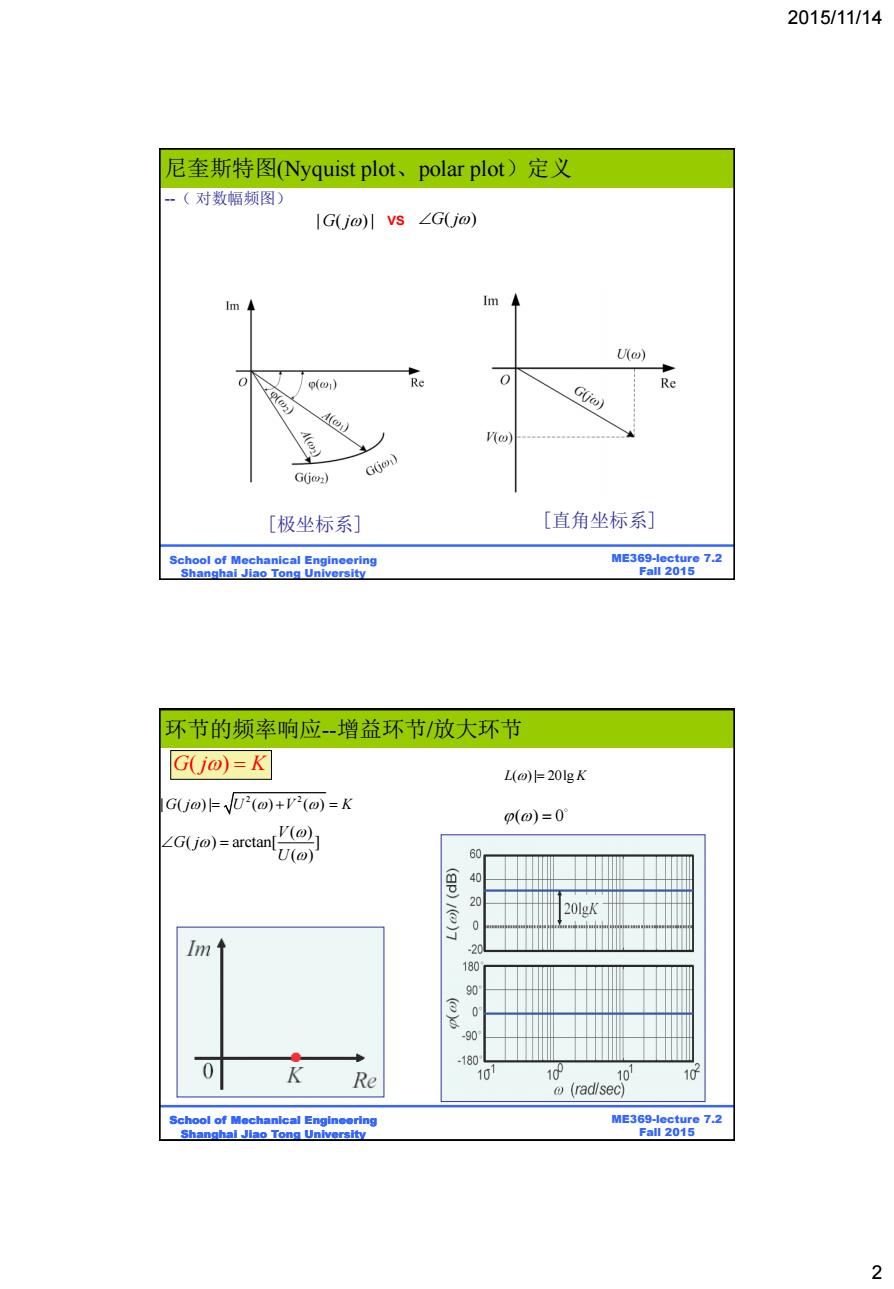
2015/11/14 尼奎斯特图Nyquist plot、polar plot)定义 一（对数幅频图） IGjo)lvs∠G(Ujo) lm◆ Im Uo) 9(1) Re 0 Re G(jw) G60m) GG2） [极坐标系] [直角坐标系] School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 环节的频率响应-增益环节/放大环节 G(jo)=K L(@)=201g K G(j@)FU-(@)+V2(@)=K p(o)=0° ∠G(jo)=arctan V(@) U(a) 14420 0 201gK Im 20 180 0 -90 -180 0 K Re 0 10 10 10 (rad/sec) School of Mechanical Engineering ME369-lecture 7.2 Shanghal Jiao Tong University Fall 2015 2

2015/11/14 2 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 尼奎斯特图(Nyquist plot、polar plot）定义 [极坐标系] [直角坐标系] --（ 对数幅频图） | ( ) | G j VS G j ( )  BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University G j K ( )   2 2 | ( ) | ( ) ( ) G j U V K       ( ) ( ) arctan[ ] ( ) V G j U      L K ( ) | 20lg    ( ) 0  环节的频率响应--增益环节/放大环节

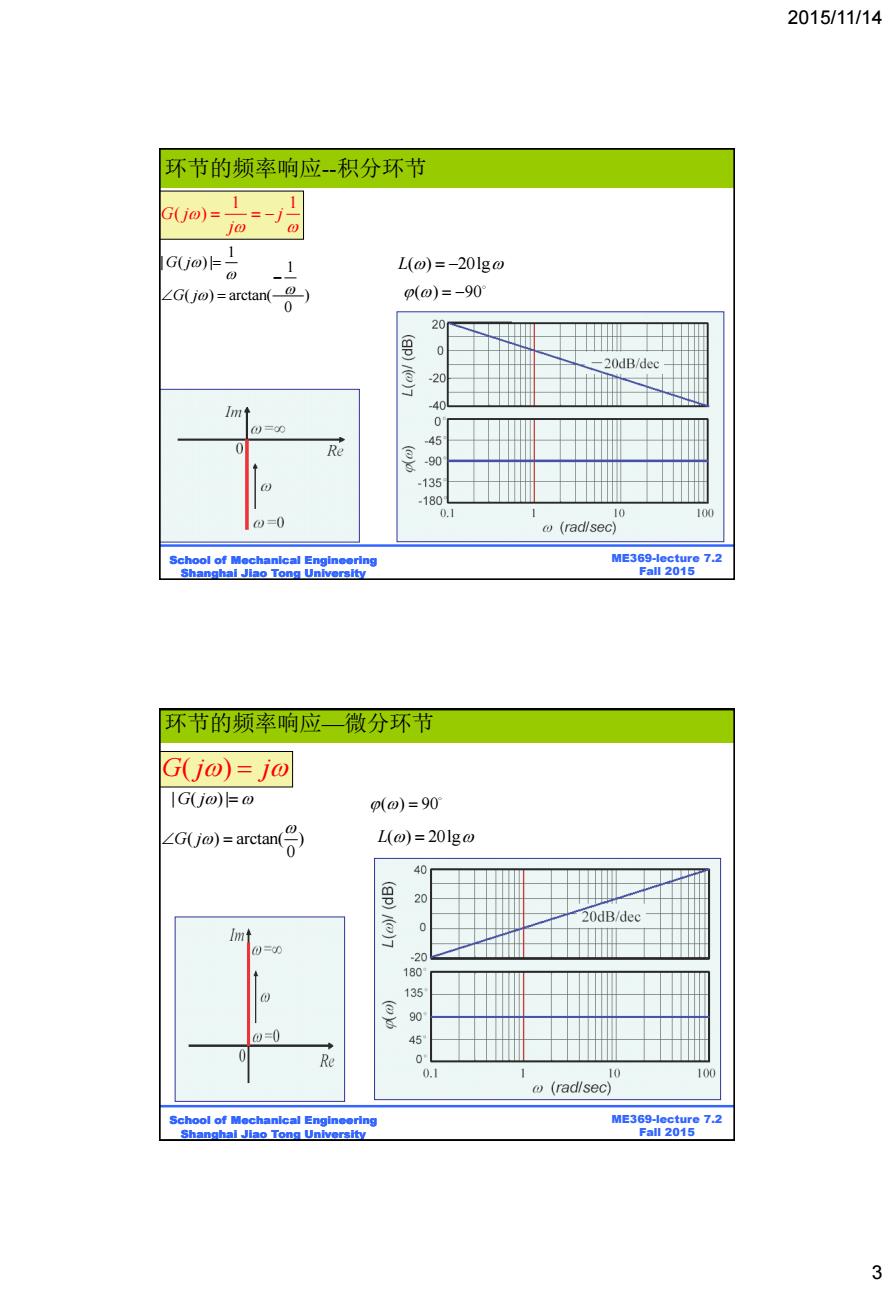
2015/11/14 环节的频率响应-积分环节 1 Gj0)==-j G(j@)1 1 L(@)=-201g@ ∠Gjo)=arctan(-o-） p(@)=-90° 0 0 20dB/dec Imt 40 0=0 0 e 悬 % -90 -180 0.1 10 100 0=0 w (radlsec) School of Mechanical Engineering ME369-lecture 7.2 Shanghal Jiao Tong University Fall 2015 环节的频率响应一微分环节 G(jo)=j@ G(j@)=@ p(o)=90 G(jo)=arctan( L(@)=201g@ 20dB/dec Imt 0 0=0 -20 180 1 90 0=0 45 0 Re 0 0.1 10 100 (radisec) School of Mechanical Engineering ME369-lecture 7.2 Shanghal Jiao Tong University Fall 2015 3

2015/11/14 3 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 1 G j j ( ) j       1 | ( ) | G j   1 ( ) arctan( ) 0 G j      L( ) 20lg      ( ) 90   环节的频率响应--积分环节 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University G j j ( )    | ( ) | G j  ( ) arctan( ) 0 G j     L( ) 20lg     ( ) 90  环节的频率响应—微分环节

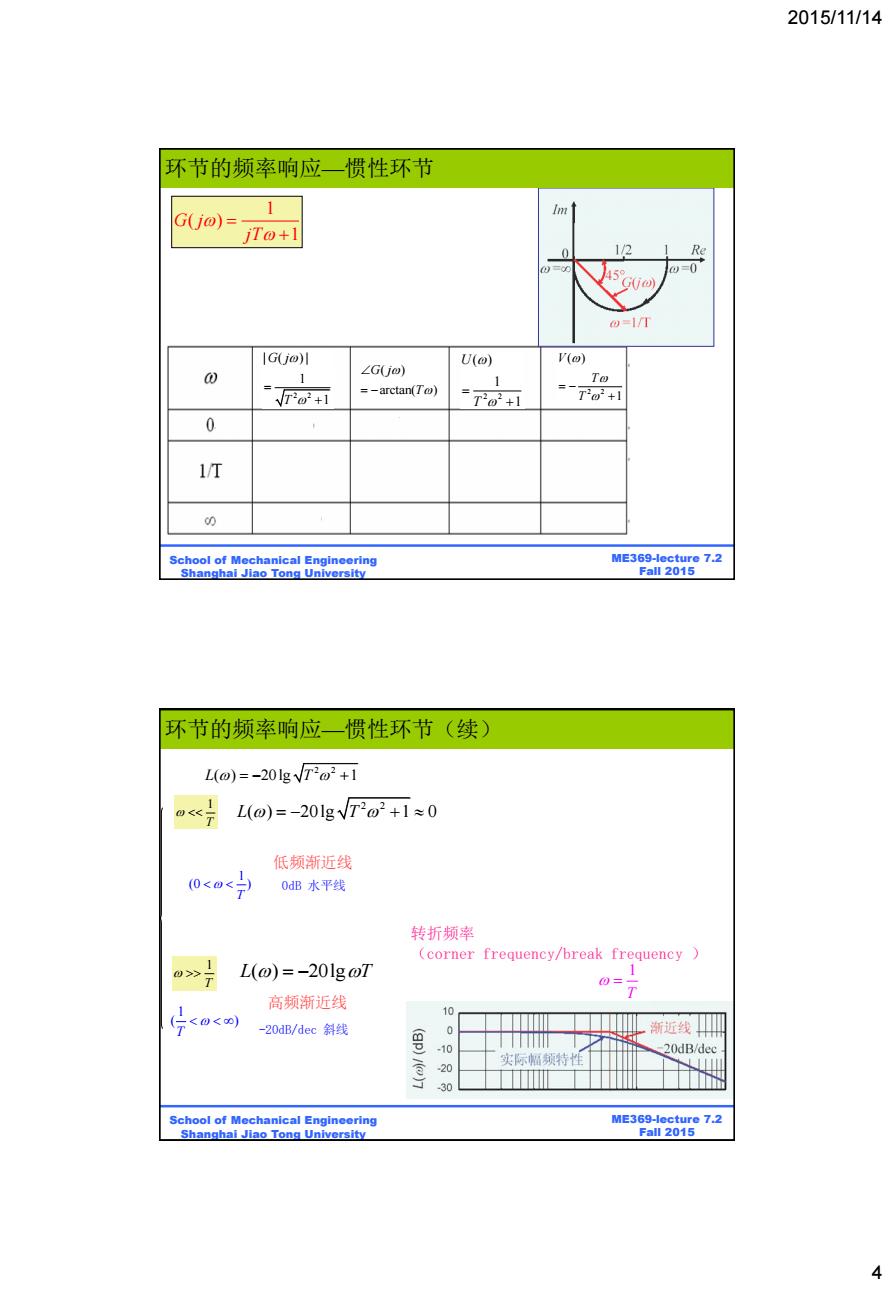
2015/11/14 环节的频率响应一惯性环节 1 G(jo)= iTo+l 0 1/2 Re 0=00 45 l@=0" G(j o=1/T 1Gjo)川 U(o) () 0 ∠GUw) 1 1 To r2a2+1 =-arctan(To) T2o2+1 T2o2+1 0 1/T 00 School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 环节的频率响应一惯性环节（续） L(@)=-20lgTo+1 L(@)=-20lgVF2o2+1≈0 低频渐近线 0<<宁 0dB水平线 转折频率 (corner frequency/break frequency 1 L(@)=-201g @T 高频渐近线 02个 10 -20dB/dec斜线 0 渐近线吗 -10 -20dB/dec 20 实际幅频特性 I 30 School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 4

2015/11/14 4 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 ( ) 1 G j jT     ( ) arctan( ) G j T      2 2 | ( ) | 1 1 G j T     2 2 ( ) 1 1 U T     2 2 ( ) 1 V T T       环节的频率响应—惯性环节 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 2 2 L T ( ) 20lg 1      1 T   2 2 L T ( ) 20lg 1 0       L T ( ) 20lg     1 T   低频渐近线 1 (0 ) T    1 ( ) T     0dB 水平线 -20dB/dec 斜线 转折频率 （corner frequency/break frequency ） 1 T   高频渐近线 环节的频率响应—惯性环节（续）

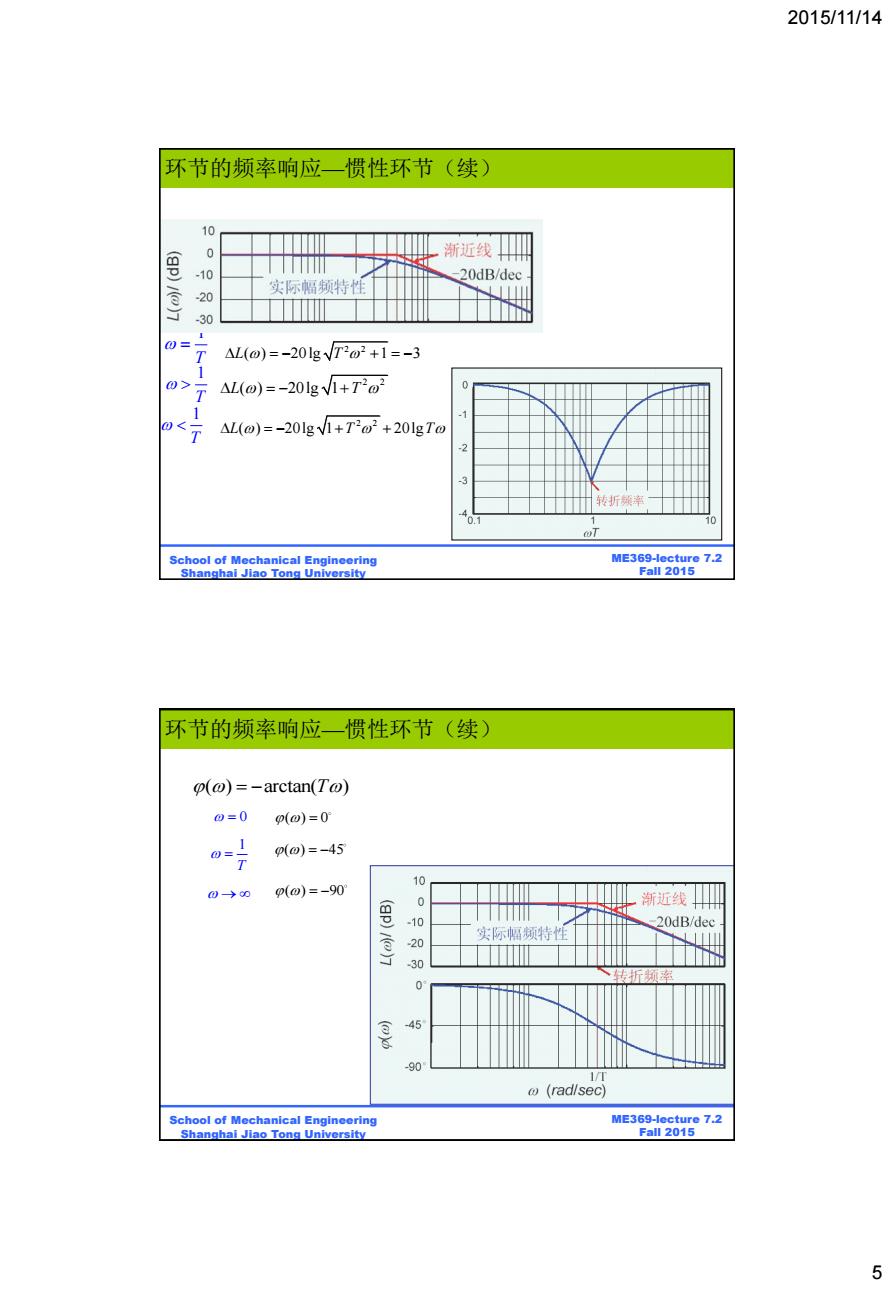
2015/11/14 环节的频率响应一惯性环节（续） 0 渐近线吗 0 20dB/dec 名 实际幅频特性 -30 0= △L(o)=-20lg√To2+1=-3 0> T AL(@)=-201gv1+T22 AL(@)=-201gv1+T@2+20lgT@ -3 转折频率 A0 School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fal12015 环节的频率响应一惯性环节（续） (@)=-arctan(T@) 0=0 0(0)=0 p(o)=-45 0→0 p(0)=-90° 0 (gp)/)7 - mm 渐近线皿 -20dB/dec 20 实际幅频特性 30 转折频率 是 -45 90 1/T @(radlsec) School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 5

2015/11/14 5 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 2 2     L T ( ) 20lg 1   1 T   1 T   2 2      L T T ( ) 20lg 1 20lg    1 T   2 2       L T ( ) 20lg 1 3   环节的频率响应—惯性环节（续） BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University    ( ) arctan( )   T  ( ) 0   1 T    ( ) 45    ( ) 90     0 环节的频率响应—惯性环节（续）

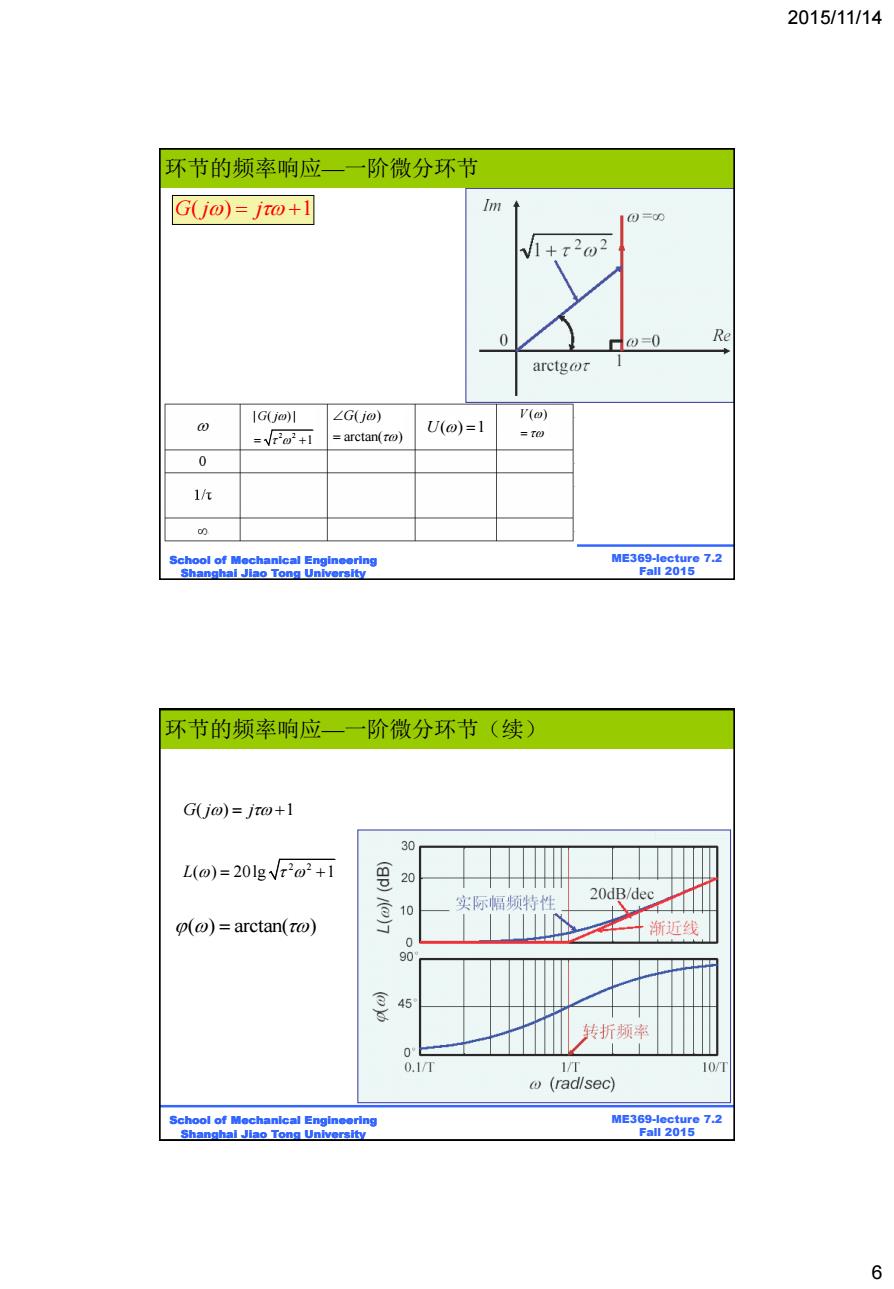
2015/11/14 环节的频率响应一一 阶微分环节 G(j@)=jw@+1 Im 0=00 0 =0 Re arctgor IG(j@)川 ∠G(jo) V() 0 =√F2o2+i arctan(ro) U(o)=1 =t0 0 lh 00 School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 环节的频率响应一一阶微分环节（续） G(j@)=jt@+1 30 L(@)=201gv202+1 (gp)/)7 20 10 实际幅频特性 20dB/dec (@)arctan(ro) 渐近线 9 是 45 转折频率 0" 0.1/T 1/T 10T (radlsec) School of Mechanical Engineering ME369-lecture 7.2 Shanghal Jiao Tong University Fall 2015 6

2015/11/14 6 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) arctan( ) G j   2 2  | ( ) | 1 G j     G j j ( ) 1     V ( )    U( ) 1   环节的频率响应—一阶微分环节 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University    ( ) arctan( )  2 2 L( ) 20lg 1      G j j ( ) 1     环节的频率响应—一阶微分环节（续）

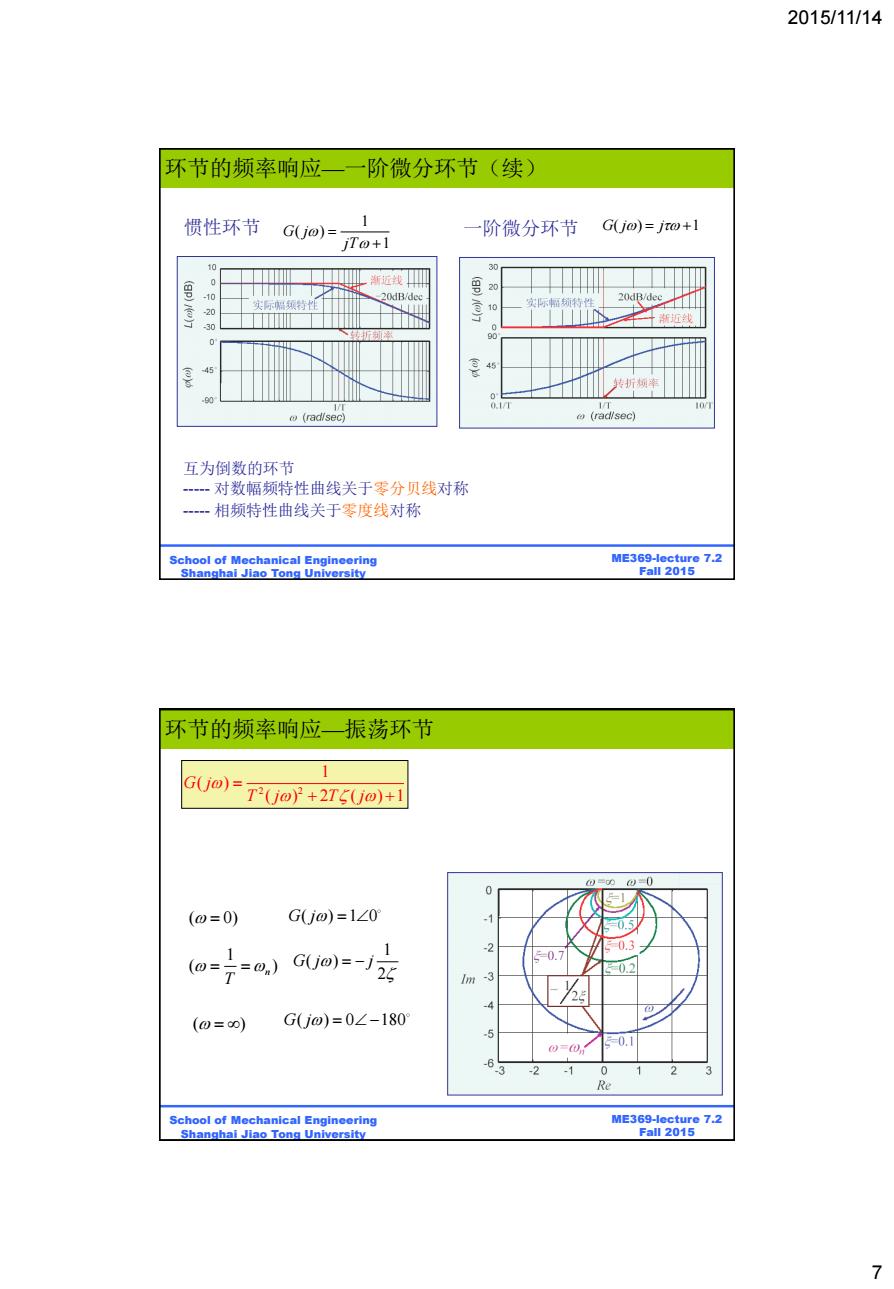
2015/11/14 环节的频率响应一一阶微分环节（续） 惯性环节 1 G(jo)= 阶微分环节 G(j@)=jt@+1 jT@+1 30 (p)/o)7 20dB/dee 20 际幅须特性 10 实际城特性 20ddee∠ 30 渐近线 0 转折率 10 (radisec) 互为倒数的环节 -对数幅频特性曲线关于零分贝线对称 -一相频特性曲线关于零度线对称 School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 环节的频率响应一振荡环节 1 G(j0)= T2(jo2+2T5(jo)+1 )0 (0=0) Gjo)=1∠0 1 G(jo)--J2G =0.3 -0.7 0.2 (0=o) Gj@)=0∠-180 0=0 0.1 2 -1 Re School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 7

2015/11/14 7 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 惯性环节 一阶微分环节 G j j ( ) 1     1 ( ) 1 G j jT     互为倒数的环节 ----- 对数幅频特性曲线关于零分贝线对称 ----- 相频特性曲线关于零度线对称 环节的频率响应—一阶微分环节（续） BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 2 2 1 ( ) ( ) 2 ( ) 1 G j T j T j        ( )   ( 0)   G j ( ) 1 0    1 ( ) n T     1 ( ) 2 G j j     G j ( ) 0 180     环节的频率响应—振荡环节

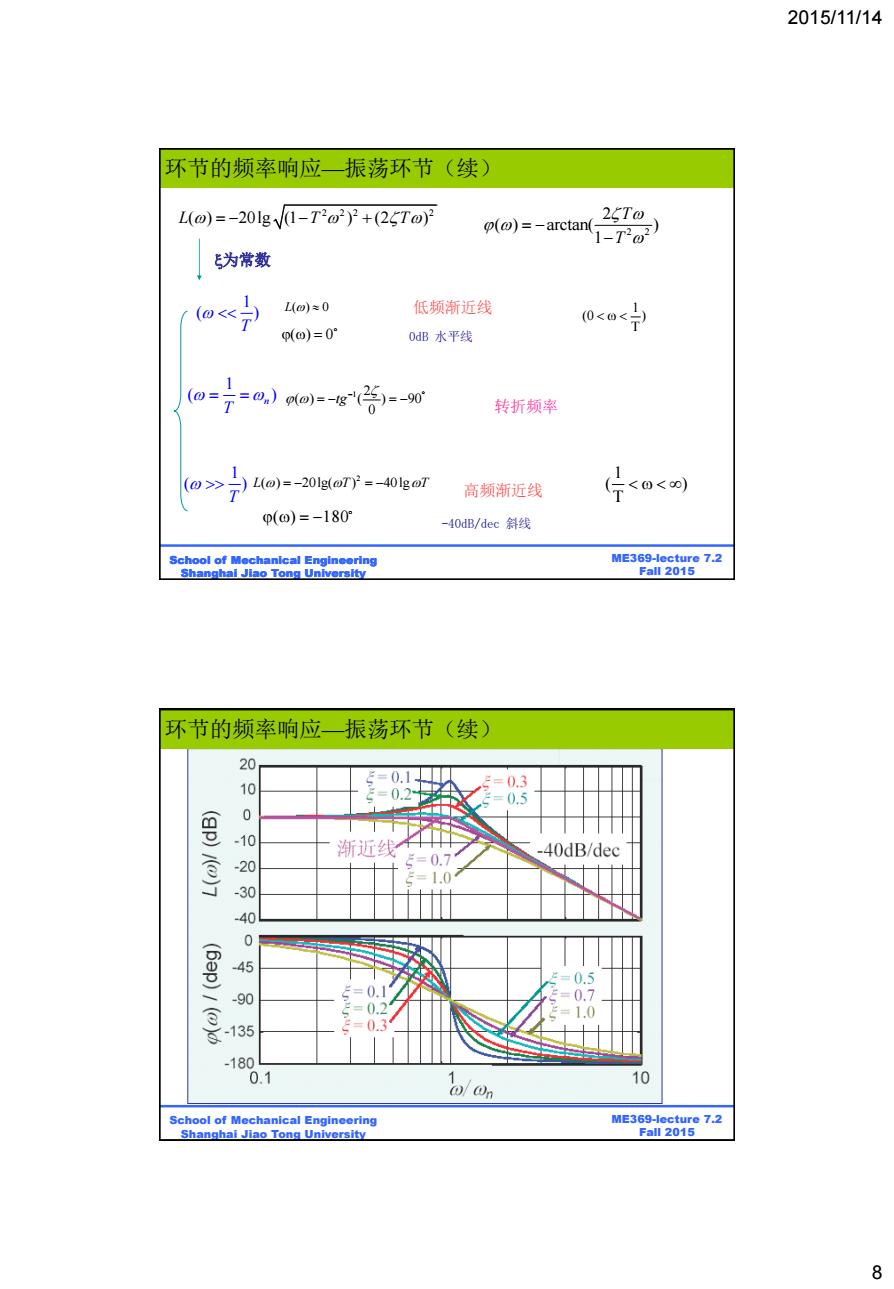
2015/11/14 环节的频率响应一振荡环节（续） L(o)=-20lgV1-T2o2)2+(25To)2 (@)=-arctan 25T0 1-72） E为常数 (0） L(@)=-201g(OT)=-401goT 高频渐近线 (片<<0) p(o)=-180° -40dB/dec斜线 School of Mechanical Engineering ME369-lecture 7.2 Shanghal Jiao Tong University Fall 2015 环节的频率响应一振荡环节（续） 00 0.1 =0.3 =0.2 =0.5 0 -10 渐近线 40dB/dec 00 =0.7 2=1.0 0 40 135 -180 0.1 1 10 @/0n School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 8

2015/11/14 8 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 为常数 2 2 2 2 L T T ( ) 20lg (1 ) (2 )         1 ( ) T   L( ) 0   2 L T T ( ) 20lg( ) 40lg        1 ( ) T   1 ( ) n T     ) T 1 (0   ) T 1 (    低频渐近线 0dB 水平线 -40dB/dec 斜线 转折频率 高频渐近线 2 2 2 ( ) arctan( ) 1 T T          ()  0 1 2 ( ) ( ) 90 0          tg  ()  180 环节的频率响应—振荡环节（续） BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 环节的频率响应—振荡环节（续）

2015/11/14 环节的频率响应一振荡环节（续） dIG(j@)1=0 E=0.05 1 do 0.20 0.25 0.3 0. 40 谐振须率 2 0.5 0,.=0vV-25 =0.707 1.00 谐振峰值 M.=A(0,)= 25V1-52 00.20.40.60.811.21.41.61.82 /①n School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 环节的频率响应一振荡环节（续） 00m L(w)=-20lg 1-(巴PT+(25”)?+201g(巴y O 20 0.20 025 =0.40 0.80 0 0.90 0.707 1.00 0.1 10 School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 9

2015/11/14 9 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 2 1 2    r n   2 1 ( ) 2 1 M A r r       谐振峰值 谐振频率 d | ( ) | 0 d G j   环节的频率响应—振荡环节（续） BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 2 2 2 ( ) 20lg [1 ( ) ] (2 ) n n L            2 2 2 2 ( ) 20lg [1 ( ) ] (2 ) 20lg( ) n n n L                 n   n 环节的频率响应—振荡环节（续）

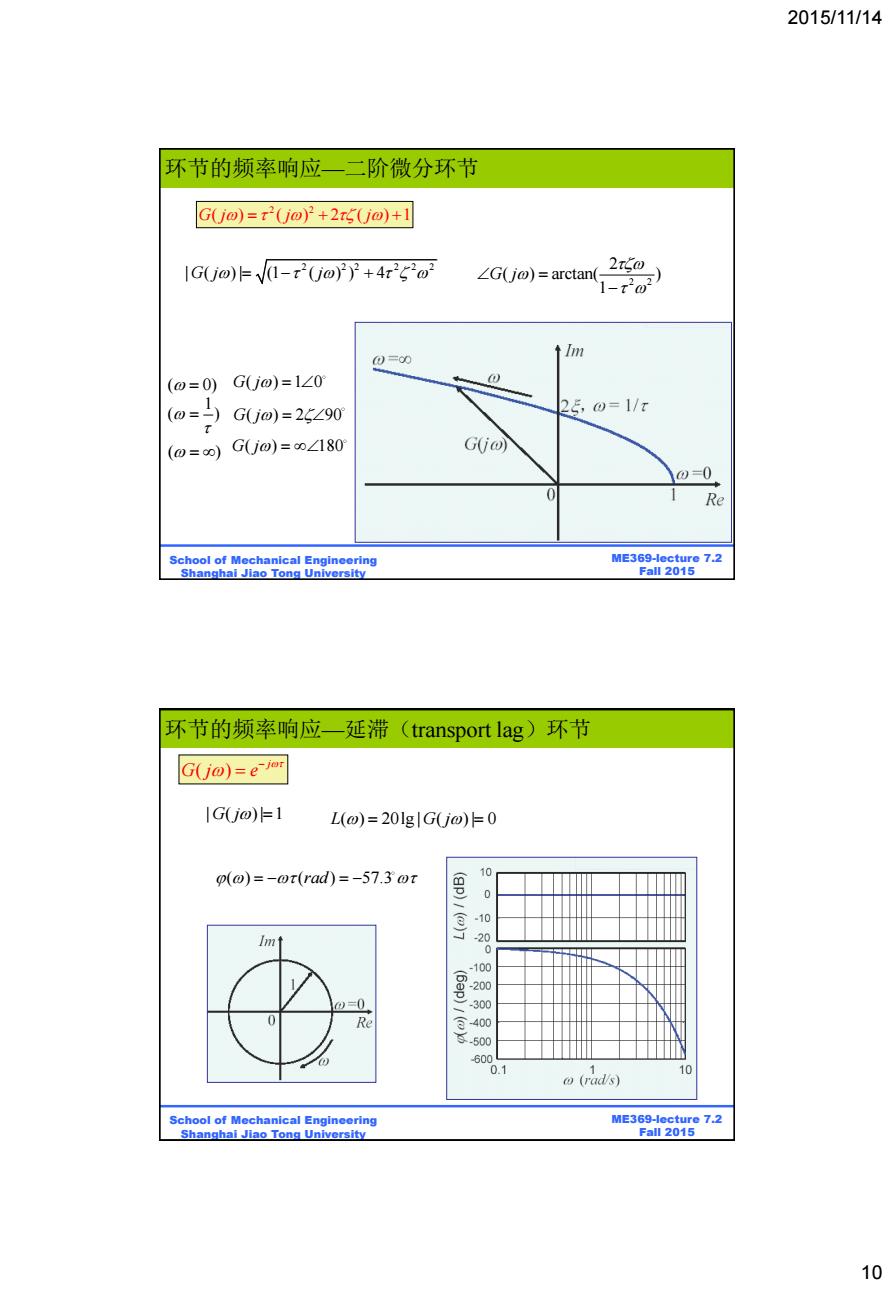
2015/11/14 环节的频率响应一二阶微分环节 GU@)=t2Uo)}2+2r5(U@)+1 lG(j@)F(1-r(joYY+4r'o ∠G(jo)=arctan 2to I-ro) 0=0 ↑m (o=0)Gjo)=1∠0 1 (@=-)Gjo)=25∠90 25,0=1/π (o=o)G(jo)=o∠180 G@) 0=0 Re School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 环节的频率响应一延滞(transport lag)环节 G(jo)=el IG(j@)=1 L(@)=201g|G(j@)0 p(@)=-or(rad)=-57.3 @r 10 (gp)/()7 0 lm↑ 2 0=0 Re 500 60 0.1 o (rad's) School of Mechanical Engineering ME369-lecture 7.2 Shanghai Jiao Tong University Fall 2015 10

2015/11/14 10 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 2 2 G j j j ( ) ( ) 2 ( ) 1         2 2 2 2 2 2 | ( ) | (1 ( ) ) 4 G j j          2 2 2 ( ) arctan( ) 1 G j        ( )   ( 0)   G j ( ) 1 0    1 ( )    G j ( ) 2 90     G j ( ) 180    环节的频率响应—二阶微分环节 BE315-Lecture 7.2 Fall 2011 ME369-lecture 7.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) j G j e         ( ) ( ) 57.3     rad | ( ) | 1 G j  L G j ( ) 20lg | ( ) | 0     环节的频率响应—延滞（transport lag）环节