
1.(10分) 分别求图1(a)和图1(b)所示系统的稳态误差。 nt)=1(t) r(t)=0 20 10 c(n) (S-10(s+2) S 图1a n(t)=t r(t)=1 10 c(t) 20 (S+10)(s+2) 2.图1b 1.解答 (a)有外界扰动引起的系统框图变为 n(t)=1(t) 10 c(t) 20 (S+10)(s+2) Cn(s) 10(s-10(s+2) (1分) N(s))sS-10(s+2)+200
1. (10 分) 分别求图 1(a)和图 1(b)所示系统的稳态误差。 图 1a 2. 图 1b 1. 解答 (a)有外界扰动引起的系统框图变为 ( 10)( 2) 200 10( 10)( 2) ( ) ( ) s s s s s N s s n C (1 分) s 10 n(t) 1(t) c(t) ( 10)( 2) 20 s s + c(t) s 10 n(t) t r(t) 1 ( 10)( 2) 20 s s + ( 10)( 2) 20 s s s 10 n(t) 1(t) r(t) 0 c(t)
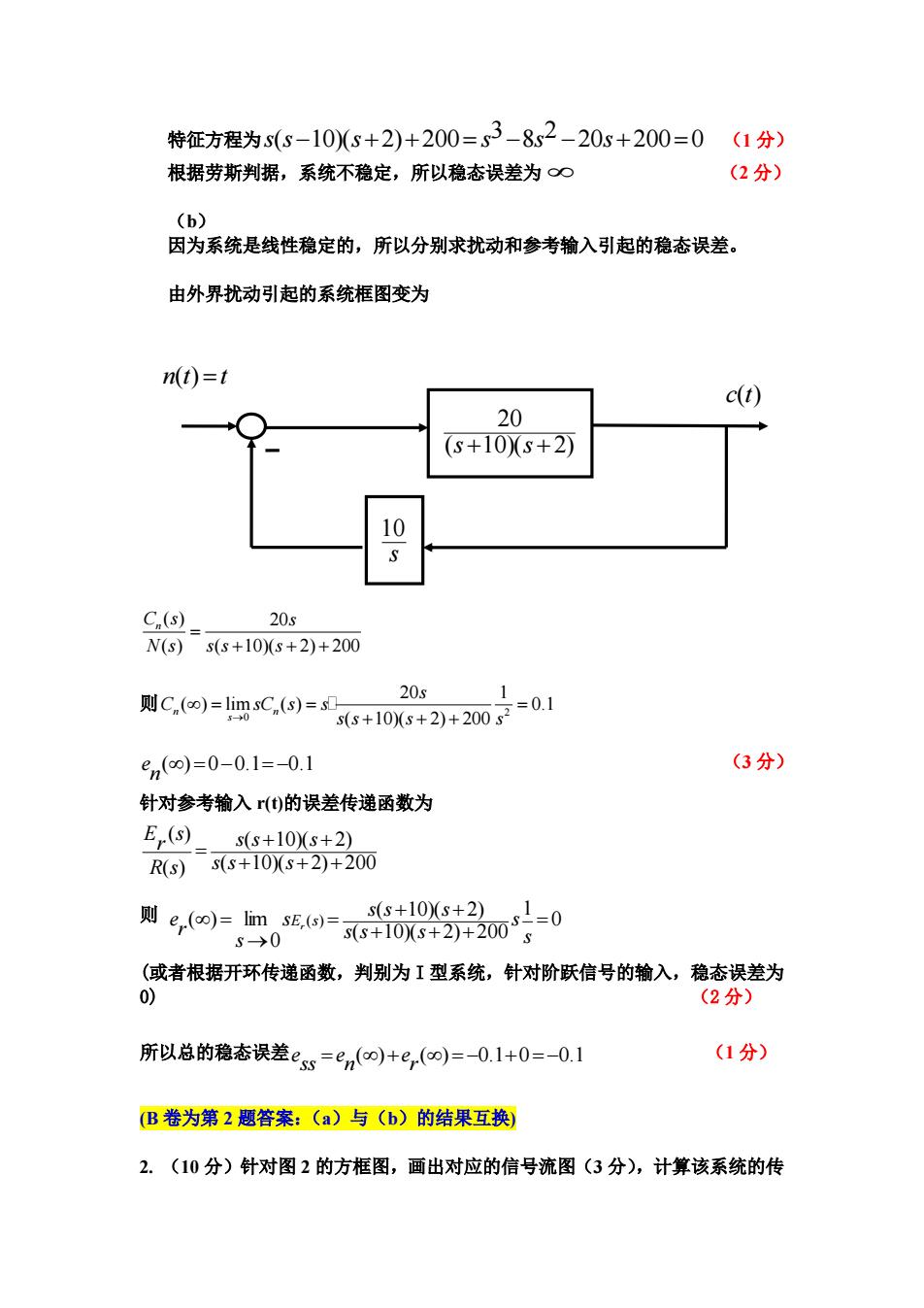
特征方程为5(5-10(5+2)+200=S3-82-205+200=0 (1分) 根据劳斯判据,系统不稳定,所以稳态误差为○ (2分) (b) 因为系统是线性稳定的,所以分别求扰动和参考输入引起的稳态误差。 由外界扰动引起的系统框图变为 n(t)=t c(t) 20 (S+10(S+2) 10 C,(s) 20s N(s)s(s+10)(s+2)+200 则Cn(o)=limsC(s)=s 20s =0.1 s(s+10)(s+2)+20032 en(∞)=0-0.1=-0.1 (3分) 针对参考输入r(t)的误差传递函数为 E,(S)_ss+10(s+2) R(s)s(S+10)(S+2)+200 则e,四-。5周80Y2m片0 S>0 (或者根据开环传递函数,判别为I型系统,针对阶跃信号的输入,稳态误差为 0) (2分) 所以总的稳态误差es=en(o)+e,(o)=0.1+0=-0.1 (1分) (B卷为第2题答案:(a)与(b)的结果互换) 2.(10分)针对图2的方框图,画出对应的信号流图(3分),计算该系统的传
特征方程为 20 200 0 2 8 3 s(s10)(s2)200 s s s (1 分) 根据劳斯判据,系统不稳定,所以稳态误差为 (2 分) (b) 因为系统是线性稳定的,所以分别求扰动和参考输入引起的稳态误差。 由外界扰动引起的系统框图变为 ( ) 20 ( ) ( 10)( 2) 200 C s n s N s s s s 则 2 0 20 1 ( ) lim ( ) 0.1 ( 10)( 2) 200 n n s s C sC s s s s s s () 00.1 0.1 n e (3 分) 针对参考输入 r(t)的误差传递函数为 ( 10)( 2) 200 ( 10)( 2) ( ) ( ) s s s s s s R s s r E 则 0 1 ( 10)( 2) 200 ( 10)( 2) 0 ( ) lim ( ) s s s s s s s s s s r e E s r (或者根据开环传递函数,判别为 I 型系统,针对阶跃信号的输入,稳态误差为 0) (2 分) 所以总的稳态误差 () () 0.100.1 r e n e ss e (1 分) (B 卷为第 2 题答案:(a)与(b)的结果互换) 2. (10 分)针对图 2 的方框图,画出对应的信号流图(3 分),计算该系统的传 c(t) s 10 n(t) t ( 10)( 2) 20 s s
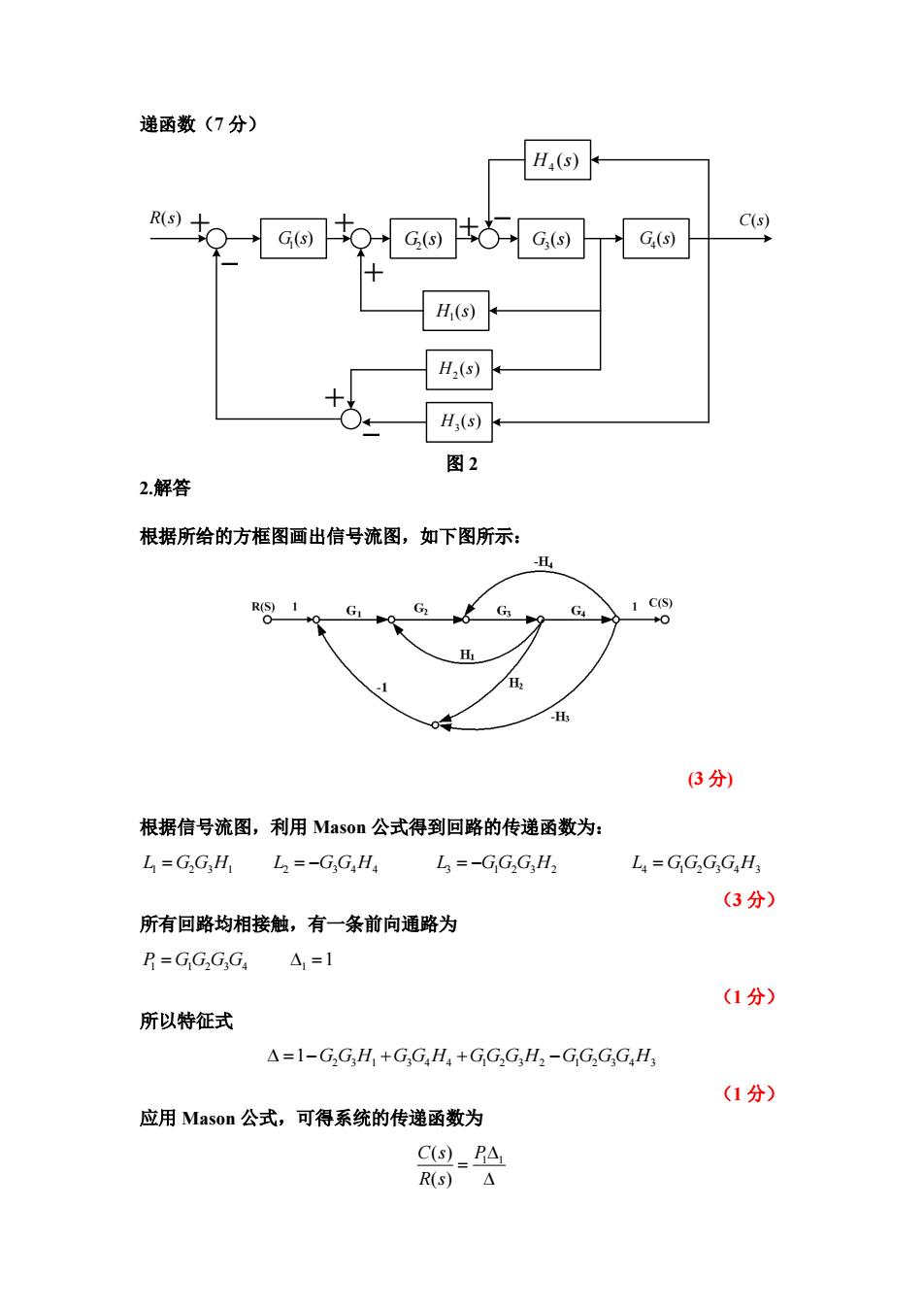
递函数(7分) H4(s) R(s) C(s) G(s) C(s) G(s) G(s) H,(s) H2(s) H,(s) 图2 2.解答 根据所给的方框图画出信号流图,如下图所示: H R(S) G G G4 1C(S) 0 H H 3分) 根据信号流图,利用Mason公式得到回路的传递函数为: L=G,GH L=-GGH L=-GG2GH2 L=GGGG,H3 (3分) 所有回路均相接触,有一条前向通路为 P=GGGGa △1=1 (1分) 所以特征式 A=1-G,GH+GGHa+GGGH2-GG2GGaHs (1分) 应用Mason公式,可得系统的传递函数为 C(s)PA R(s)△
递函数(7 分) ( ) 1 G s ( ) 2 G s ( ) 3 G s ( ) 4 G s ( ) 1 H s ( ) 2 H s ( ) 3 H s ( ) 4 H s R(s) C(s) 图 2 2.解答 根据所给的方框图画出信号流图,如下图所示: (3 分) 根据信号流图,利用 Mason 公式得到回路的传递函数为: L G G H 1 2 3 1 L G G H 2 3 4 4 L G G G H 3 1 2 3 2 L G G G G H 4 1 2 3 4 3 (3 分) 所有回路均相接触,有一条前向通路为 P G G G G 1 1 2 3 4 1 1 (1 分) 所以特征式 2 3 1 3 4 4 1 2 3 2 1 2 3 4 3 1 G G H G G H G G G H G G G G H (1 分) 应用 Mason 公式,可得系统的传递函数为 1 1 ( ) ( ) C s P R s
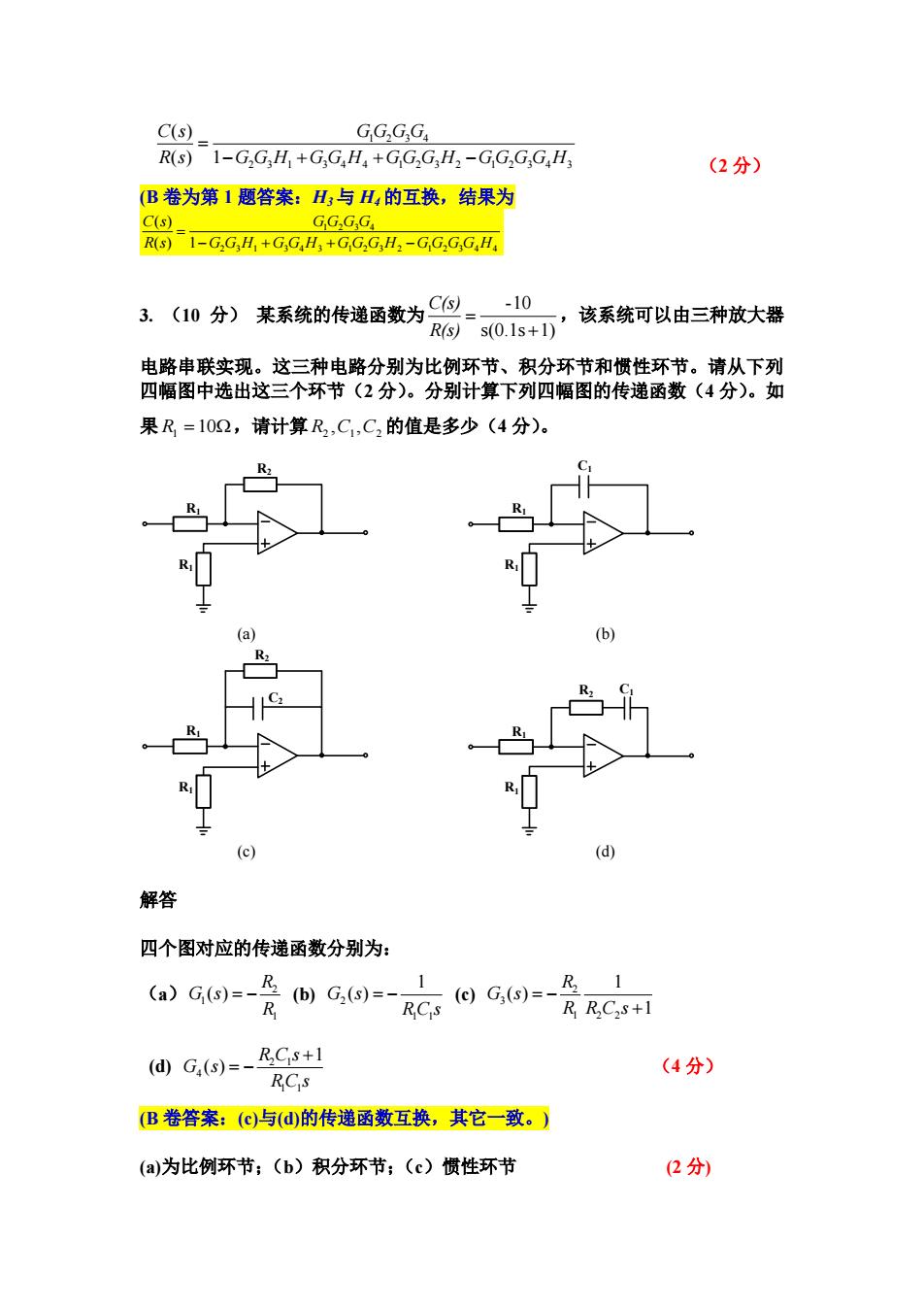
C(s) GG,G.Gx R(s)1-G,G,Hj+GG,H3+GG2GH2-GG2G,GH3 (2分) (B卷为第1题答案:H,与H4的互换,结果为 C(s) GG,G,Ga R(s) 1-GG H+GG H3+GG2G,H2-GG2G,GHa 3.(10分)某系统的传递函数为C--10 该系统可以由三种放大器 Rs)s(0.1s+1) 电路串联实现。这三种电路分别为比例环节、积分环节和惯性环节。请从下列 四幅图中选出这三个环节(2分)。分别计算下列四幅图的传递函数(4分)。如 果R=102,请计算R2,C,C2的值是多少(4分)。 (a c (d) 解答 四个图对应的传递函数分别为: (a)G)=-G=-日G=-& 1 R RCs R RC2s+1 (d)G(s)=- RCs+1 (4分) RCs (B卷答案:(c)与(@的传递函数互换,其它一致。) (a)为比例环节;(b)积分环节;(c)惯性环节 (2分)
1 2 3 4 2 3 1 3 4 4 1 2 3 2 1 2 3 4 3 ( ) ( ) 1 C s G G G G R s G G H G G H G G G H G G G G H (2 分) (B 卷为第 1 题答案:H3 与 H4 的互换,结果为 2 3 1 3 4 3 1 2 3 2 1 2 3 4 4 1 2 3 4 ( ) 1 ( ) G G H G G H G G G H G G G G H G G G G R s C s 3. (10 分) 某系统的传递函数为 s(0.1s 1) -10 R(s) C(s) ,该系统可以由三种放大器 电路串联实现。这三种电路分别为比例环节、积分环节和惯性环节。请从下列 四幅图中选出这三个环节(2 分)。分别计算下列四幅图的传递函数(4 分)。如 果 R1 10 ,请计算 2 1 2 R ,C ,C 的值是多少(4 分)。 R1 R1 R2 R1 R1 C1 (a) (b) R1 R1 C2 R2 R1 R1 R2 C1 (c) (d) 解答 四个图对应的传递函数分别为: (a) 2 1 1 ( ) R G s R (b) 2 1 1 1 G s( ) R C s (c) 2 3 1 2 2 1 ( ) 1 R G s R R C s (d) 2 1 4 1 1 1 ( ) R C s G s R C s (4 分) (B 卷答案:(c)与(d)的传递函数互换,其它一致。) (a)为比例环节;(b)积分环节;(c)惯性环节 (2 分)
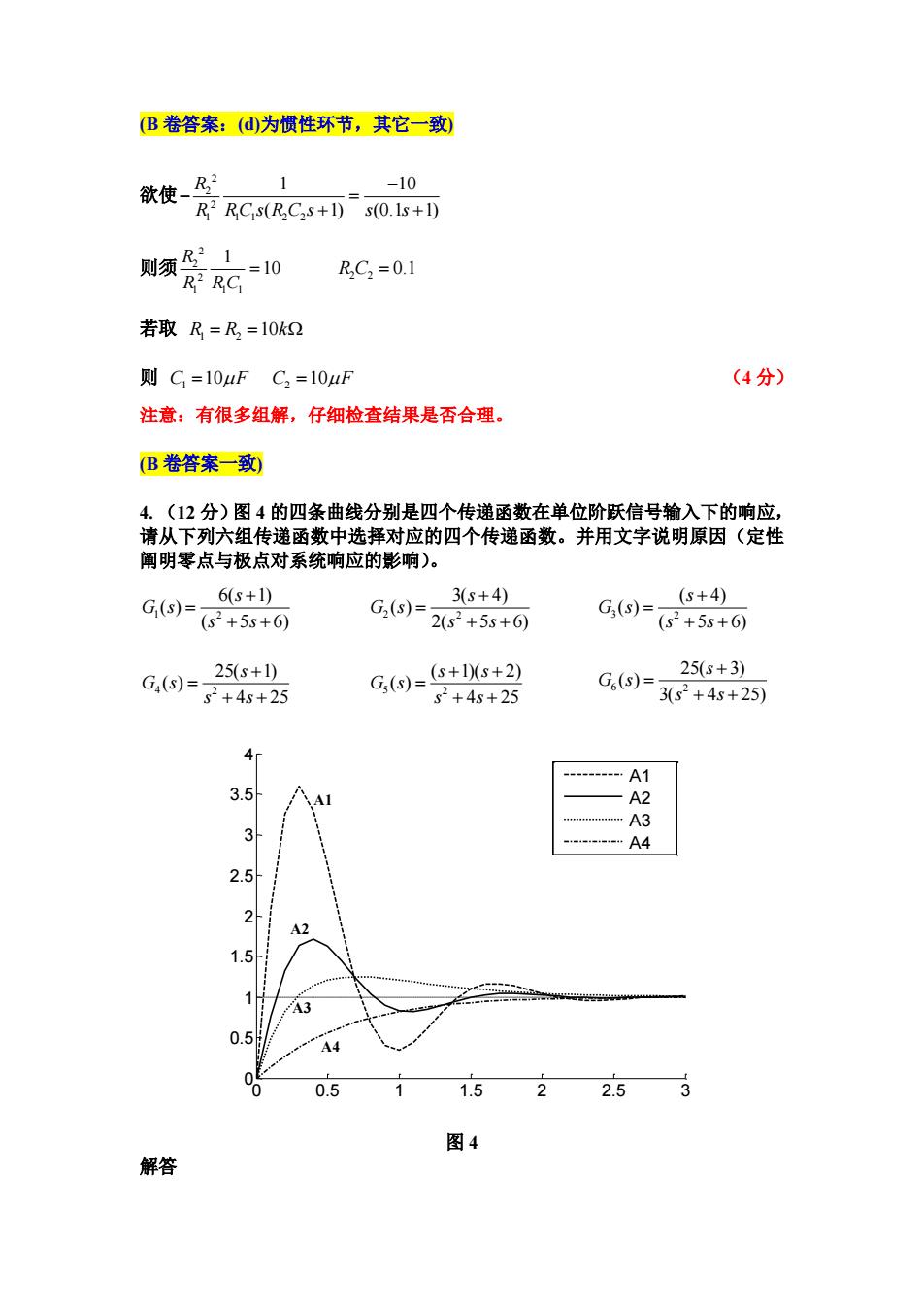
(B卷答案:(d为惯性环节,其它一致) 欲使、飞2 1 -10 R2 RC s(R,C2s+1)s(0.1s+1) 则须飞1 =10 RC2=0.1 R2 RC 若取R=R=10k2 则C=10uFC2=10uF (4分) 注意:有很多组解,仔细检查结果是否合理。 (B卷答案一致) 4.(12分)图4的四条曲线分别是四个传递函数在单位阶跃信号输入下的响应, 请从下列六组传递函数中选择对应的四个传递函数。并用文字说明原因(定性 阐明零点与极点对系统响应的影响)。 3(s+4) G(S)= 6(s+1) G(s)= G3(S)= (S+4) (s2+5s+6) 2(s2+5s+6) (s2+5s+6) G,(S)= 25(s+1) G,()=s+1s+2) 25(s+3) G6(S)= s2+4s+25 s2+4s+25 3(s2+4s+25) 4 A1 3.5 A2 A3 A4 2.5 A2 1.5 43 0.5 A4 0 0.5 1.5 2.5 图4 解答
(B 卷答案:(d)为惯性环节,其它一致) 欲使 2 2 2 1 1 1 2 2 1 10 ( 1) (0.1 1) R R R C s R C s s s 则须 2 2 2 1 1 1 1 10 R R R C 2 2 R C 0.1 若取 1 2 R R k 10 则 1 C F 10 2 C F 10 (4 分) 注意:有很多组解,仔细检查结果是否合理。 (B 卷答案一致) 4. (12 分)图 4 的四条曲线分别是四个传递函数在单位阶跃信号输入下的响应, 请从下列六组传递函数中选择对应的四个传递函数。并用文字说明原因(定性 阐明零点与极点对系统响应的影响)。 1 2 6( 1) ( ) ( 5 6) s G s s s 2 2 3( 4) ( ) 2( 5 6) s G s s s 3 2 ( 4) ( ) ( 5 6) s G s s s 4 2 25( 1) ( ) 4 25 s G s s s 5 2 ( 1)( 2) ( ) 4 25 s s G s s s 6 2 25( 3) ( ) 3( 4 25) s G s s s 0 0.5 1 1.5 2 2.5 3 0 0.5 1 1.5 2 2.5 3 3.5 4 A1 A2 A3 A4 A1 A2 A3 A4 图 4 解答

每个对应关系及原因分析(3分) A1对应G4:因为A1包含振荡成分,为欠阻尼系统,所以传递函数的根在s 平面中有虚部(在时域表现形式上存在三角函数成分)。考察各个传递函数的极 点,发现G4.G5.G6的极点有虚部。进一步考量,A1终值为1,所以传递函数增 益为1,排除G5 比较G4和G6,G4的零点s=-1比G6的零点s=-3更靠近虚轴,所以引起的超调 量更大。A1的超调量最大,所以对应的传递函数为G4.(3分) (B卷答案:题且中G2与G4的传递函数互换了,所以解答中只需把G2与G4互 换,其它一致.A1对应G2) A2对应G6:分析基本如上,只是因为A2超调量没有A1大,所以G6符合要求。 (3分) (B卷答案一致) A3对应G,因为A3不包含振荡成分,为过阻尼系统,所以传递函数的根在s 平面中的实轴上(在时域表现形式上不存在三角函数成分,只有指数成分)。考 察各个传递函数的极点,发现G1,G2,G3的极点在实轴上。进一步考量,A3终值 为1,所以传递函数增益为1,排除G3 比较G1和G2,G1的零点s=-1比G2的零点s=-4更靠近虚轴,所以引起的超调 量更大。A3的超调量比A4大,所以A3对应的传递函数为G1.(3分) (B卷答案一致) A4对应G2:分析基本如上,只是因为A4超调量没有A3大,所以G2符合要求。 (3分) (B卷答案:A4对应G4,其它一致) 注意:主要考察学生是否了解闭环极点不在实轴上(有虚部),以及在实轴上(无 虚部)的响应特点,分别是振荡(欠阻尼)和不振荡(过阻尼)的曲线。 零点对于过阻尼二阶系统:越靠近原点超调越大。 零点对于欠阻尼二阶系统:越靠近原点超调越大。 5.(15分)针对图5(a)的质量-弹簧阻尼系统。其中外力F为阶跃信号,x,为 输出,定义为距离平衡点的位移。参数为:F1kg,仁10N.s/m,k仁20N/m,F=1N。 原始系统的输出与期望位移x=1(0m比较,不能完全地满足下列期望指标: 稳态误差e<0.1m,超调量6<10%,t,<0.3s(5%误差标准)。 使用单位闭环反馈控制范式,如图Fig5(b),该系统作为被控对象(plant),请 设计PD(比例小积分微分)控制器来同时实现上述每一个指标。通常PD有三 个基本的环节K。,K
每个对应关系及原因分析(3 分) A1 对应 G4: 因为 A1 包含振荡成分,为欠阻尼系统,所以传递函数的根在 s 平面中有虚部(在时域表现形式上存在三角函数成分)。考察各个传递函数的极 点,发现 G4,G5,G6 的极点有虚部。进一步考量,A1 终值为 1,所以传递函数增 益为 1,排除 G5. 比较 G4 和 G6, G4 的零点 s 1 比 G6 的零点 s 3 更靠近虚轴,所以引起的超调 量更大。A1 的超调量最大,所以对应的传递函数为 G4. (3 分) (B 卷答案:题目中 G2与 G4的传递函数互换了,所以解答中只需把 G2与 G4互 换,其它一致。 A1 对应 G2) A2 对应 G6:分析基本如上,只是因为 A2 超调量没有 A1 大,所以 G6 符合要求。 (3 分) (B 卷答案一致) A3 对应 G1:因为 A3 不包含振荡成分,为过阻尼系统,所以传递函数的根在 s 平面中的实轴上(在时域表现形式上不存在三角函数成分,只有指数成分)。考 察各个传递函数的极点,发现 G1,G2,G3 的极点在实轴上。进一步考量,A3 终值 为 1,所以传递函数增益为 1,排除 G3. 比较 G1 和 G2, G1 的零点 s 1 比 G2 的零点 s 4 更靠近虚轴,所以引起的超调 量更大。A3 的超调量比 A4 大,所以 A3 对应的传递函数为 G1. (3 分) (B 卷答案一致) A4 对应 G2:分析基本如上,只是因为 A4 超调量没有 A3 大,所以 G2 符合要求。 (3 分) (B 卷答案:A4 对应 G4,其它一致) 注意:主要考察学生是否了解闭环极点不在实轴上(有虚部),以及在实轴上(无 虚部)的响应特点,分别是振荡(欠阻尼)和不振荡(过阻尼)的曲线。 零点对于过阻尼二阶系统:越靠近原点超调越大。 零点对于欠阻尼二阶系统:越靠近原点超调越大。 5. (15 分)针对图 5 (a)的质量-弹簧-阻尼系统。其中外力 F 为阶跃信号,xo 为 输出,定义为距离平衡点的位移。参数为:m=1kg,f=10N.s/m,k=20N/m,F=1N。 原始系统的输出与期望位移 xi=1(t) m 比较,不能完全地满足下列期望指标: 稳态误差 ss e <0.1m,超调量 10%,t s s 0.3 ( 5% 误差标准)。 使用单位闭环反馈控制范式,如图 Fig 5 (b),该系统作为被控对象(plant),请 设计 PID(比例\积分\微分)控制器来同时实现上述每一个指标。通常 PID 有三 个基本的环节 K s s Ki Kp d , ,
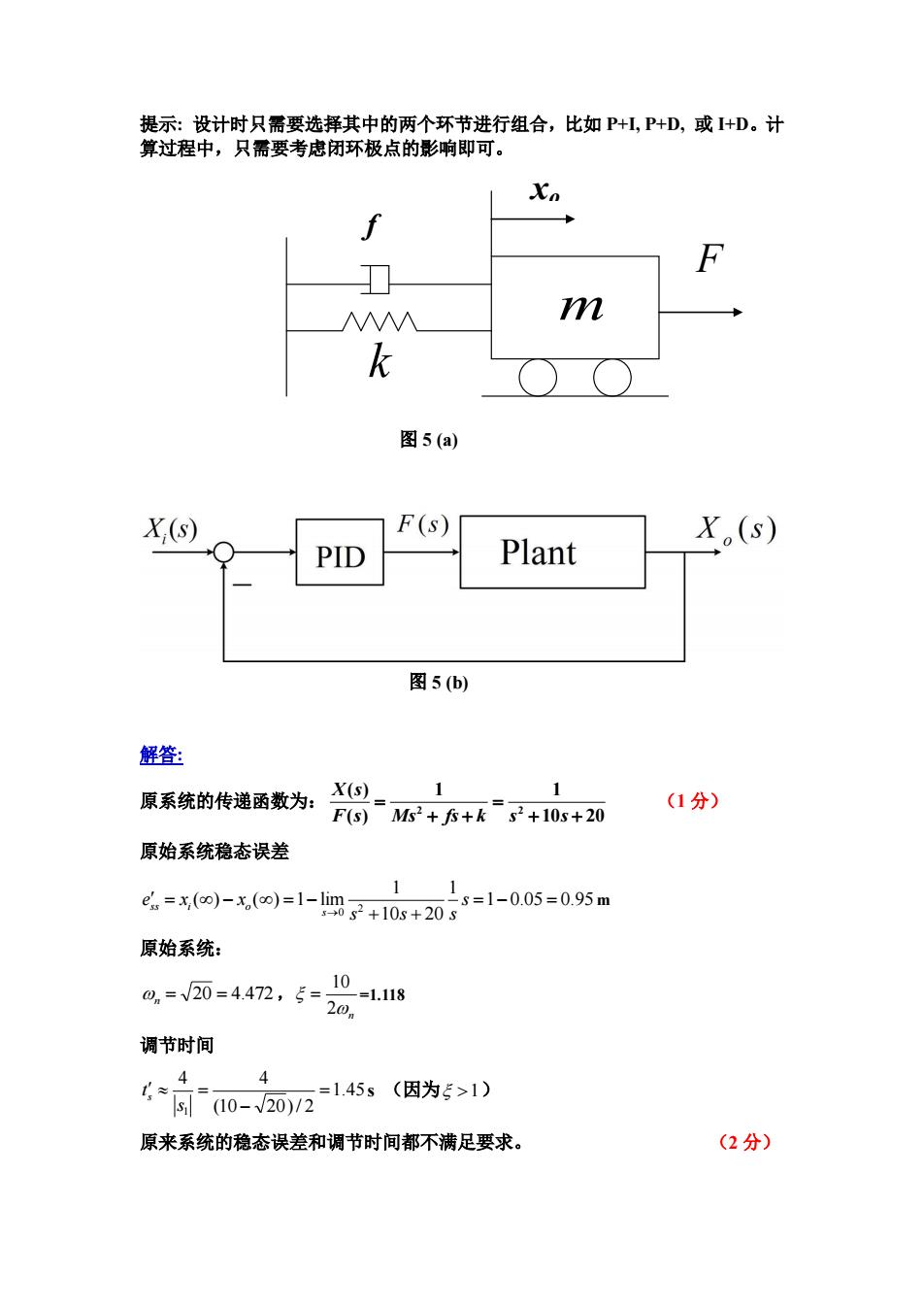
提示:设计时只需要选择其中的两个环节进行组合,比如P+L,P+D,或I+D。计 算过程中,只需要考虑闭环极点的影响即可。 M m k 图5(a) X(s) F(s) X (s) PID Plant 图5(b) 解答: 原系统的传递函数为: X=1 1 Fs)MS2+F+ks2+105+20 (1分) 原始系统稳态误差 11 e.=x(o)-x(o)=1-lm0g2+10s+20 s=1-0.05=0.95m 原始系统: 0,=20=4.472,5=2 10 -=1.118 调节时间 4 4 t≈ (10-20)/2 =1.45s(因为5>1) 原来系统的稳态误差和调节时间都不满足要求。 (2分)
提示: 设计时只需要选择其中的两个环节进行组合,比如 P+I, P+D, 或 I+D。计 算过程中,只需要考虑闭环极点的影响即可。 图 5 (a) 图 5 (b) 解答: 原系统的传递函数为: 2 2 ( ) 1 1 ( ) 10 20 X s F s Ms fs k s s (1 分) 原始系统稳态误差 1 0.05 0.95 1 10 20 1 ( ) ( ) 1 lim 2 0 s s s s e x x s ss i o m 原始系统: n 20 4.472 , n 2 10 =1.118 调节时间 1.45 (10 20)/ 2 4 4 1 s t s s (因为 1 ) 原来系统的稳态误差和调节时间都不满足要求。 (2 分) F f k m xo

减小稳态误差,减少调节时间,保证超调量,所以需要使用PD控制器。(1分) X(s) F(s) X(s) s2+10s+20 把原始的系统看作开环系统,加入比例微分控制器,并构成闭环系统。闭环系 统的结构图和传递函数分别为: X(s) KS+K。 (1分) X,(s)s2+(10+Ka)s+(20+Kn) Kas+Kp K。 1-g+10+K)s+(20+K, Kp>180N/m(2分) (20+K) =V20+K5=,10+ (2分) 220+K, 6=34=10+K4*03>3=>K>10 (2分) 2 6=e5)2.3V1-52=>5>2.3V1-2=>5>0.917 (1分) 5= 10+K>0.917>K>0.917*220+K。-10 2,20+K。 因为Kn>180,所以K>0.917*2√20+180-10=15.94Ns/m (2分) 比较t,10 最后符合要求的范围为K,>180N/m,Ka>15.94Ns/m (1分) (B卷答案一致,只是计算过程中系统输出变量x为y) 6.(20分)机械振动系统如图6a所示。当系统受到=8.9N的力的作用时,质 量为m的动块振动情况如图6b所示。试根据这个响应曲线,确定系统的m、f 和k值
减小稳态误差, 减少调节时间,保证超调量, 所以需要使用 PD 控制器。(1 分) 把原始的系统看作开环系统,加入比例微分控制器,并构成闭环系统。闭环系 统的结构图和传递函数分别为: ( ) (10 ) (20 ) ( ) 2 d p d p i o s K s K K s K X s X s (1 分) 2 0 1 lim 1 0.1 (10 ) (20 ) (20 ) d p p s d p p K s K K s K s K K m=> Kp 180 N/m (2分) 20 w K n p 10 2 20 d p K K (2 分) 0.3 3 n s w t => *0.3 3 2 10 d s K t => Kd 10 (2 分) 2 ( / 1 ) e 0.1 2 2.3 1 => 2 2.3 1 => 0.917 (1 分) 10 2 20 d p K K >0.917=> Kd 0.917*2 20 Kp 10 因为 Kp 180 , 所以 Kd 0.917*2 20 180 10 15.94 Ns/m (2 分) 比较 t s 0.3 指标下 10 Kd 最后符合要求的范围为 Kp 180 N/m, Kd 15.94 Ns/m (1 分) (B 卷答案一致,只是计算过程中系统输出变量 x 为 y) 6. (20 分)机械振动系统如图 6a 所示。当系统受到 p=8.9N 的力的作用时,质 量为 m 的动块振动情况如图 6b 所示。试根据这个响应曲线,确定系统的 m、f 和 k 值
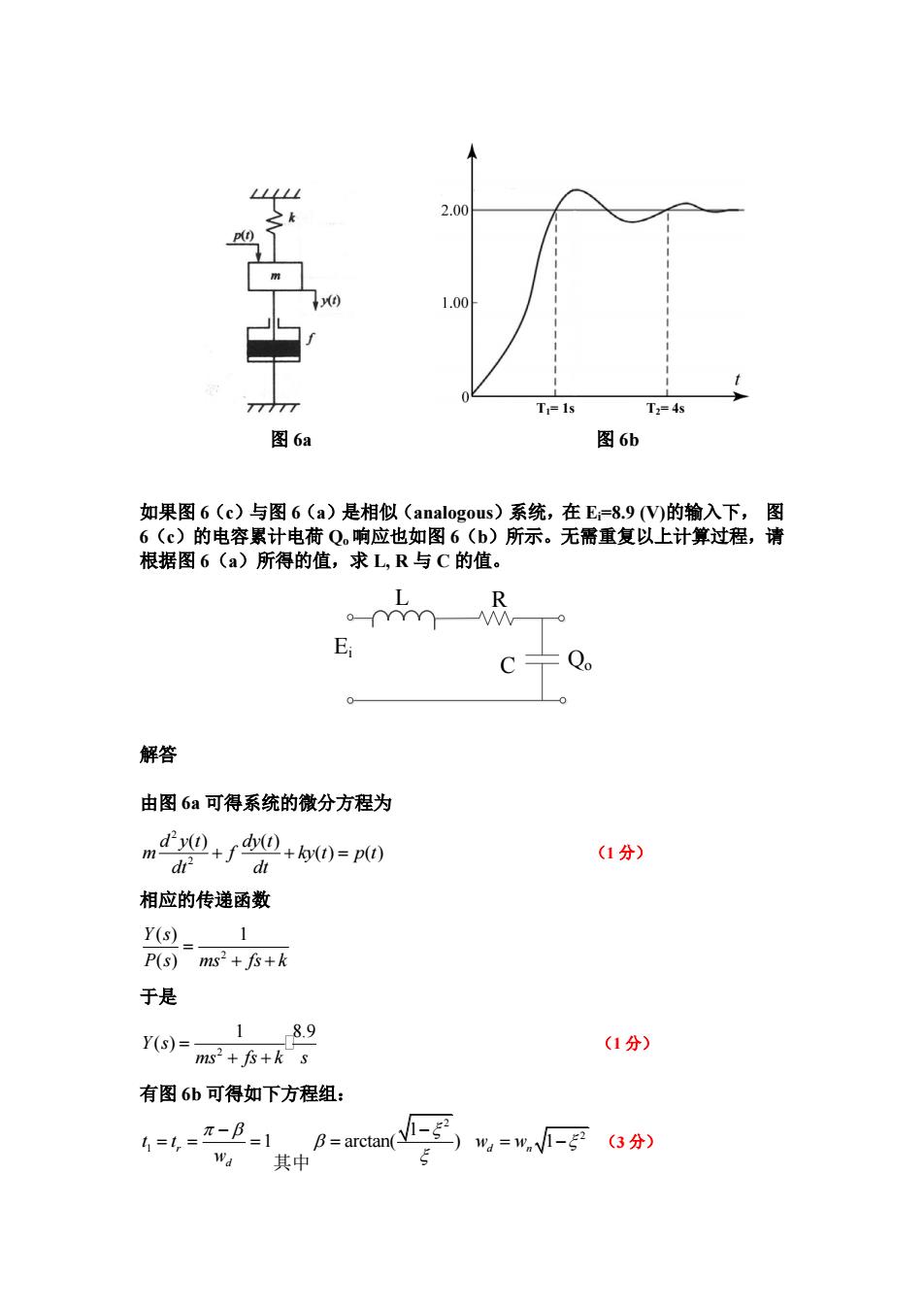
2.00 p(t) 1.00 T=1s T2=4s 图6a 图6b 如果图6(c)与图6(a)是相似(analogous)系统,在E=8.9(V的输入下,图 6(c)的电容累计电荷Q。响应也如图6(b)所示。无需重复以上计算过程,请 根据图6(a)所得的值,求L,R与C的值。 R C 解答 由图6a可得系统的微分方程为 m0+r0+0)=p0 (1分) dr 相应的传递函数 Y(s) 1 P(s)ms2+f尽+k 于是 Y(s)= 1 8.9 (1分) ms2+fs+k s 有图6b可得如下方程组: 4==-B=1g=atm-耳%=忧F (3分) wa其中
T1= 1s T2= 4s 图 6a 图 6b 如果图 6(c)与图 6(a)是相似(analogous)系统,在 Ei=8.9 (V)的输入下, 图 6(c)的电容累计电荷 Qo 响应也如图 6(b)所示。无需重复以上计算过程,请 根据图 6(a)所得的值,求 L, R 与 C 的值。 L R C Ei Qo 解答 由图 6a 可得系统的微分方程为 2 2 ( ) ( ) ( ) ( ) d y t dy t m f ky t p t dt dt (1 分) 相应的传递函数 2 ( ) 1 ( ) Y s P s ms fs k 于是 2 1 8.9 Y s( ) ms fs k s (1 分) 有图 6b 可得如下方程组: 1 1 r d t t w 其中 2 1 arctan( ) 2 1 w w d n (3 分)

2r=3 12-4= (2分) limsY(s)=lims 18.98.9 =2 (2分) 0ms2+尽+ksk 联立求的:k=4.45NWm,wn=2.425=0.5 (3分) 根据系统的特征方程 s+5+k=0 m 并对照标准二阶系统特征方程s2+25w,S+wn2=0 有:k=,2=25w, (2分) m m 可得m=0.76Kg,f=1.84N/m/s (2分) 综上分析计算,得到系统的参数为m=0.76,f=1.84,k=4.45 图6(c)所示系统傲分方程为 Ld2@+R№,@+Q0=E0 (1分) dt 90+R20+2Q0=89 dt dt 对照图6(a)的微分方程,因为相似性。 所以 1 L=m.R=f.c=k (2分) 代入m=0.76,f=1.84,k=4.45得 C=0.225F,L=0.76HR=1.842 (1分) (B卷答案一致,只是计算过程中系统输出变量y为) 7.(15分)设单位负反馈系统的开环传递函数为 K G(s)= s(1+0.1s)1+0.25s) (1)试确定闭环系统稳定时的K值范围:
2 1 2 3 d t t w (2 分) 2 0 0 1 8.9 8.9 lim ( ) lim 2 s s sY s s ms fs k s k (2 分) 联立求的: k 4.45 N/m, 2.42 wn 0.5 (3 分) 根据系统的特征方程 2 0 f k s s m m 并对照标准二阶系统特征方程 2 2 2 0 n n s w s w 有: 2 n k w m 2 n f w m (2 分) 可得 m 0.76 Kg, f 1.84 N/m/s (2 分) 综上分析计算,得到系统的参数为 m 0.76, f 1.84, k 4.45 图 6(c)所示系统微分方程为 ( ) ( ) ( ) ( ) 1 2 Q t E t dt C dQ t R dt d Q t L o i o o (1 分) ( ) 8.9 ( ) ( ) 1 2 Q t dt C dQ t R dt d Q t L o o o 对照图 6(a)的微分方程,因为相似性。 所以 k C L m R f 1 , , (2 分) 代入 m 0.76, f 1.84, k 4.45 得 C 0.225F,L 0.76H,R 1.84 (1 分) (B 卷答案一致,只是计算过程中系统输出变量 y 为 x) 7. (15 分)设单位负反馈系统的开环传递函数为 ( ) (1 0.1 )(1 0.25 ) K G s s s s (1)试确定闭环系统稳定时的 K 值范围;