上海交通大学：《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[08]Lecture64-Forced response 系统强迫响应

2015/10/21 ME369-系统模型、分析与控制 6.4系统强迫响应 School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 阶(1 st order)系统-实例 T T。+T(t) T。+T V =Rig+K MCdr_(T,+T)-(亿+D T=Ki。=Jno+bo dt R 2(s) K T(s) 1 'm(s) R(Jos+b+KK,) T(s)(MCRs+1) School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 1

2015/10/21 1 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 6.4 系统强迫响应 ME369-系统模型、分析与控制 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University + _ Vemf Ja Ra ia Vin  b V R i K in a a b    T K i J b    t a a  ( ) ( ) ( ) t in a a b t s K V s R J s b K K     T0 T T 0  b 0 T T t  ( ) T T 0  b 0 0 ( ) ( ) MC dT T T T T b dt R     ( ) 1 ( ) ( 1) b T s T s MCRs   一阶（1 st order）系统--实例

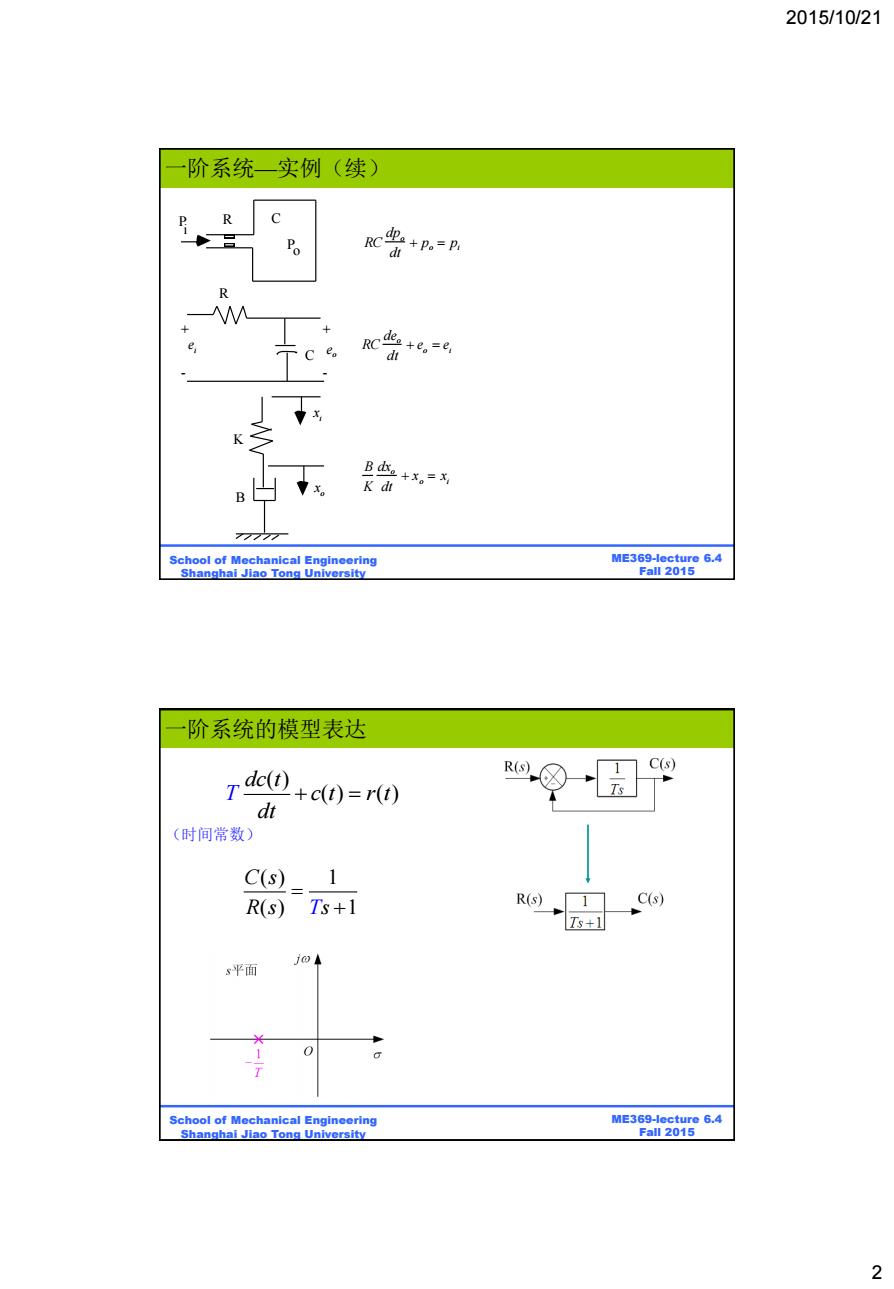
2015/10/21 阶系统一实例（续） R RC虫+p,=P d R Tce。 RC des tee dt Ba+x。二， K dt 77777 School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 阶系统的模型表达 rde(t) R() 1☐C(s dt +c(t)=(t) (时间常数) C(s) 1 R(s)Ts+1 R(s)_ 1 C(s) Ts+1 s平面 School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 2

2015/10/21 2 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University P i Po R C RC dpo dt  po  pi R C RC deo dt  eo  ei ei + - + - eo K B B K dxo dt  xo  xi xi xo 一阶系统—实例（续） ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) 1 ( ) 1 C s R s Ts   一阶系统的模型表达 （时间常数） ( ) ( ) ( ) dc t T c t r t dt  

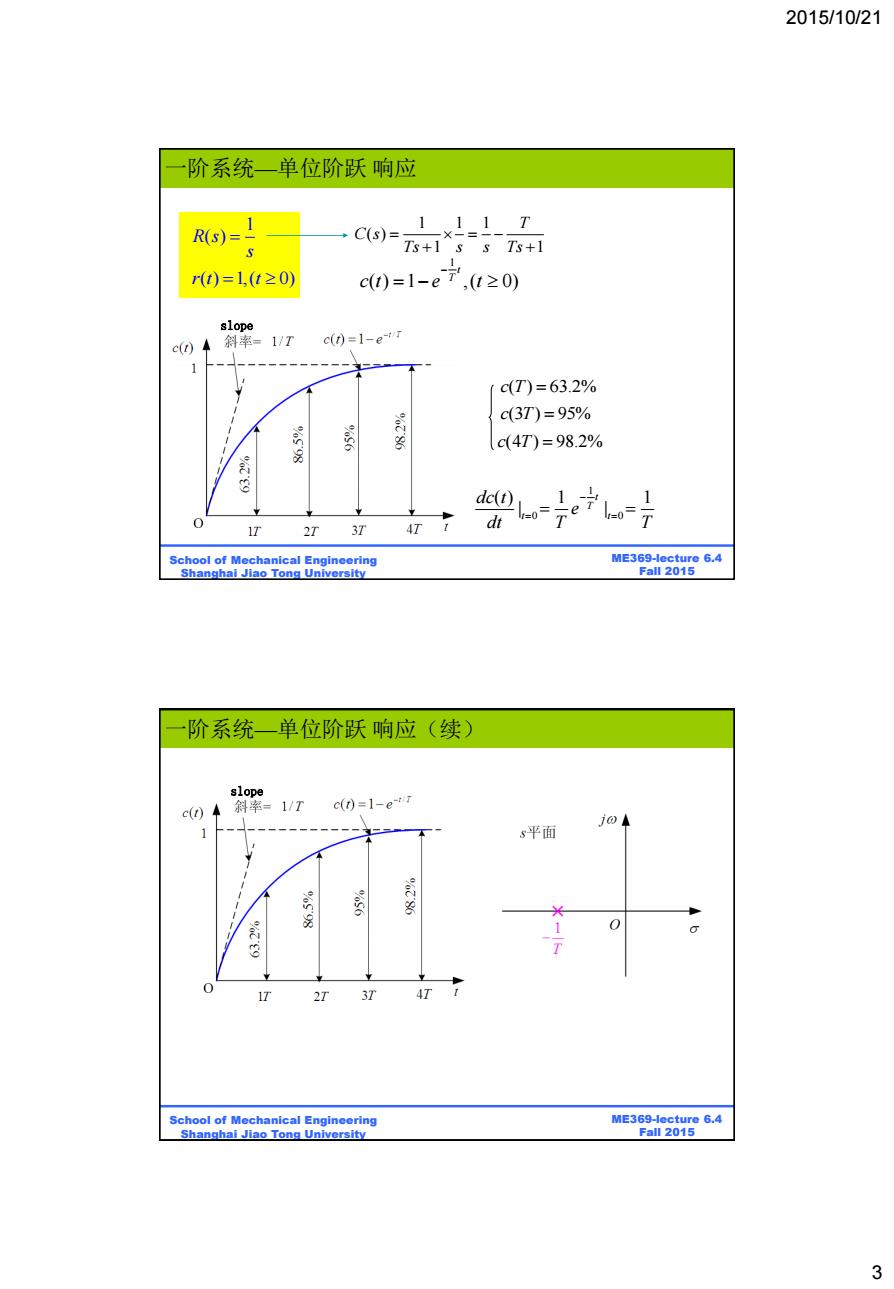
2015/10/21 阶系统一单位阶跃响应 111T R(S)=- C(s)= Ts+1s s Ts+1 t)=1,t≥0) c0=1-e7,(0≥0) slope c() 斜率-1/T c(t)=1-e-iT c(T)=63.2% c(3T)=95% c(4T)=98.2% 0 2T 3T AT dt School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 阶系统一单位阶跃响应（续） slope c(t)◆ 斜率=1/T c(0=1-et7 j04 s平面 爹 8 2T 4T School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 3

2015/10/21 3 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University slope 1 R s( ) s  1 1 1 ( ) 1 1 T C s Ts s s Ts       1 ( ) 1 ,( 0) t T c t e t    c T (3 ) 95%  c T (4 ) 98.2%  c T( ) 63.2%  1 0 0 ( ) 1 1 | | t T t t dc t e dt T T      r t t ( ) 1,( 0)   一阶系统—单位阶跃 响应 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University slope 一阶系统—单位阶跃 响应（续）

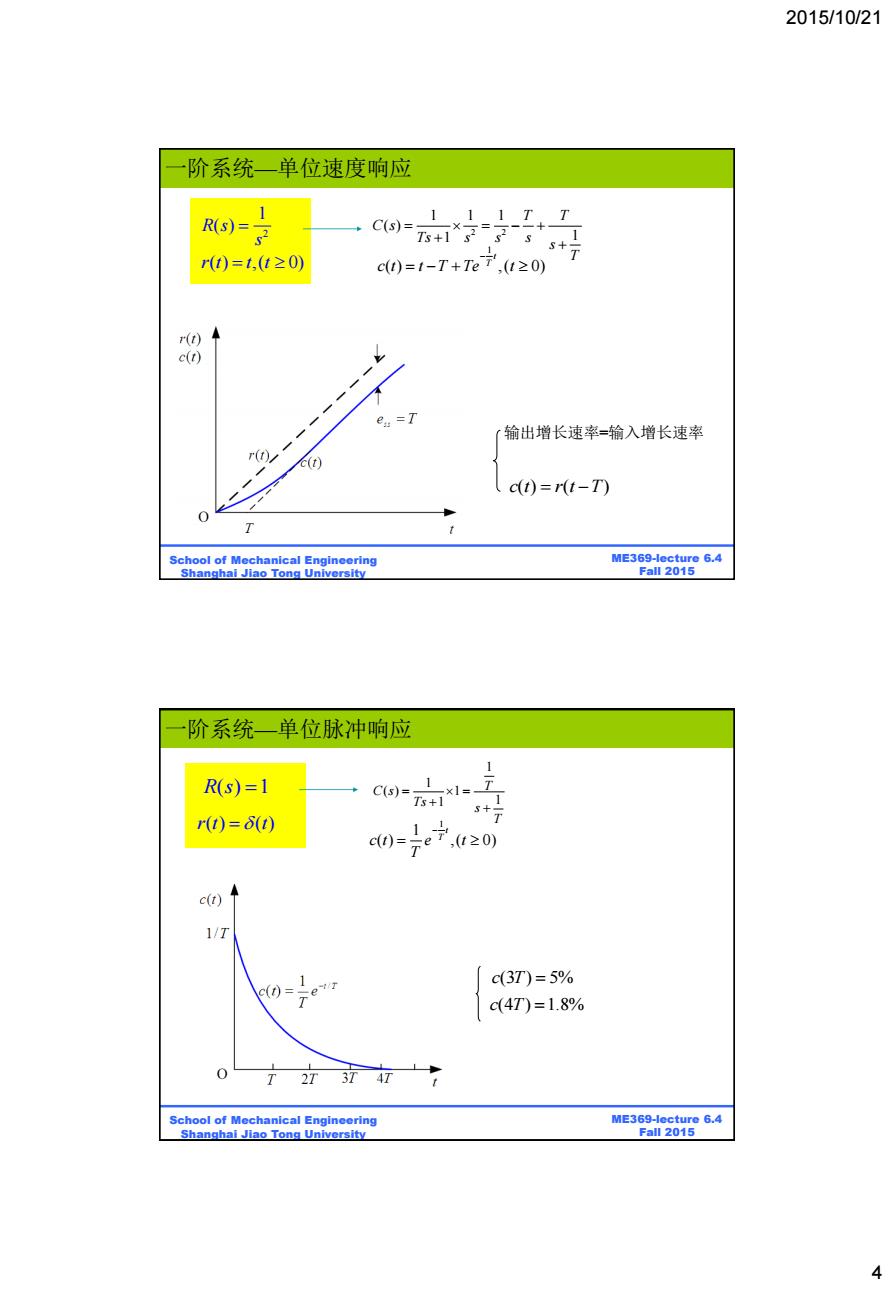
2015/10/21 阶系统一单位速度响应 R-子 1 +C(s)= 111T,T 1 rt)=t,(t≥0) c0=1-T+Te7,4≥0) r(t) c(t) e=T 输出增长速率=输入增长速率 r( c(n) c(t)=r(t-T) 0 入 t School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 阶系统一单位脉冲响应 1 R(s)=1 Cs)=1 Ts+1 1 r(t)=6t) c0=7e宁，2≥0) 1- c(t) 1/T 方ex c(3T)=5% c(4T)=1.8% T2T3747 School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 4

2015/10/21 4 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 ( ) ,( 0) t T c t t T Te t      2 1 R s( ) s  2 2 1 1 1 ( ) 1 1 T T C s Ts s s s s T        r t t t ( ) ,( 0)   输出增长速率=输入增长速率 c t r t T ( ) ( )   一阶系统—单位速度响应 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 1 ( ) ,( 0) t T c t e t T    R s( ) 1  T s T Ts C s 1 1 1 1 1 ( )      r t t ( ) ( )   c T (3 ) 5%  c T (4 ) 1.8%  一阶系统—单位脉冲响应

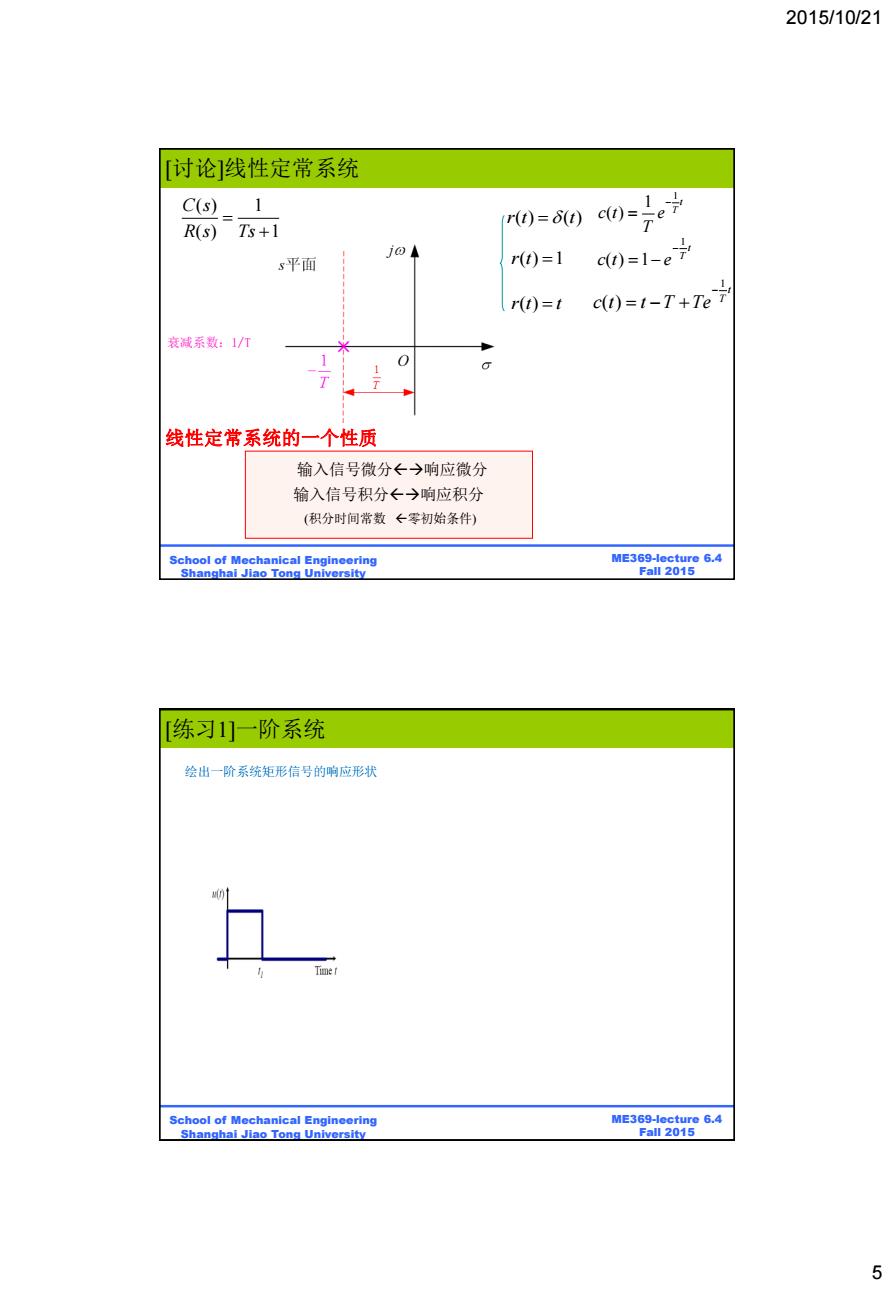
2015/10/21 [讨论]线性定常系统 C(s)1 r(t)=6t) c(t)= R(s)Ts+1 T j⊙◆ s平面 r(t)=1 c0=1-e r(t)=t c0=1-T+7e 衰减系数：1/T 线性定常系统的一个性质 输入信号微分←→响应微分 输入信号积分←→响应积分 (积分时间常数←零初始条件) School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 练习1]一阶系统 绘出一阶系统矩形信号的响应形状 School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 5

2015/10/21 5 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 1 ( ) t T c t e T   1 ( ) t T c t t T Te     t T c t e 1 ( ) 1    ( ) 1 ( ) 1 C s R s Ts   衰减系数：1/T r t t ( )  r t( ) 1  r t t ( ) ( )   输入信号微分响应微分 输入信号积分响应积分 (积分时间常数 零初始条件) 线性定常系统的一个性质 [讨论]线性定常系统 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [练习1]一阶系统 绘出一阶系统矩形信号的响应形状

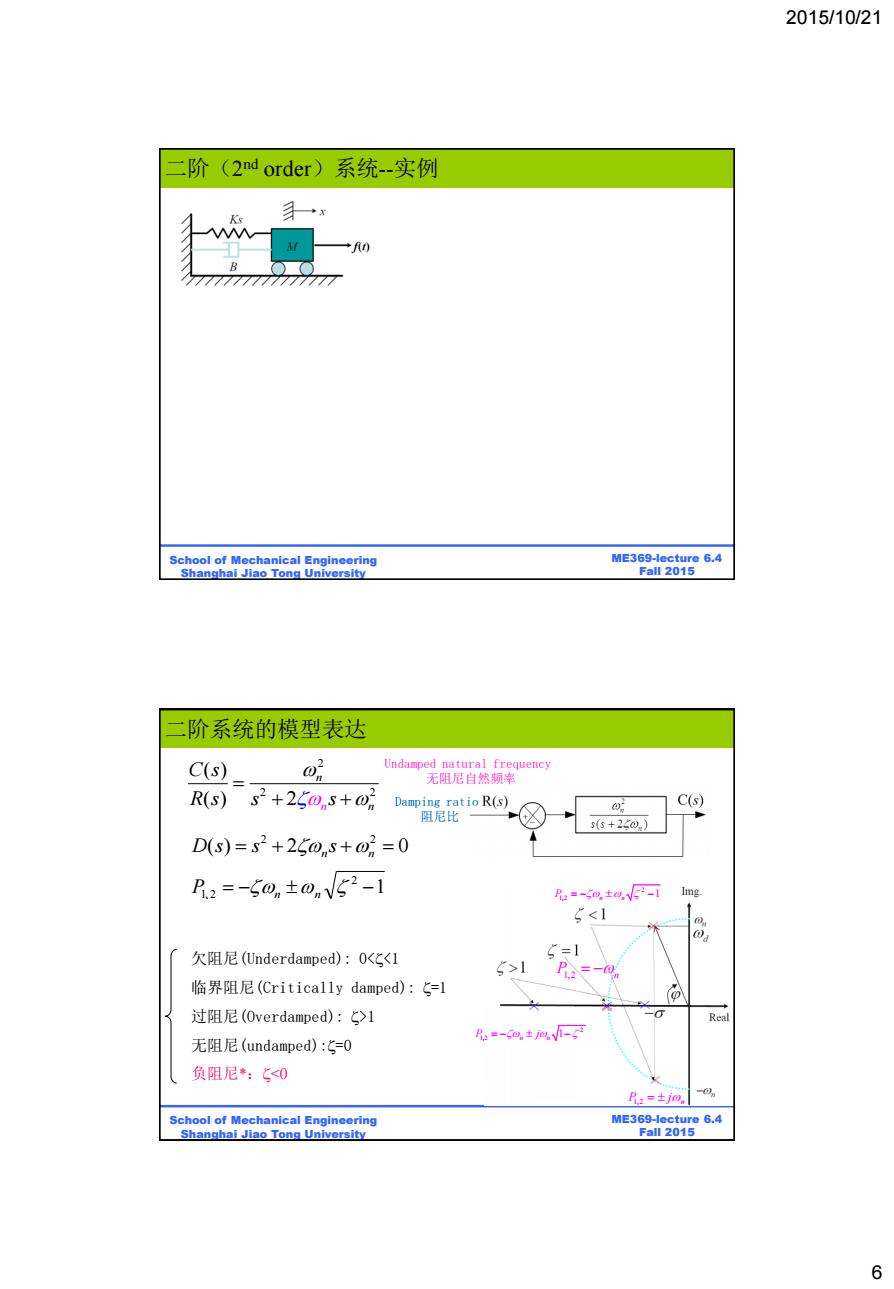
2015/10/21 二阶(2 nd order)系统-实例 手一x School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 阶系统的模型表达 C(s) o Undamped natural frequency 无阻尼自然频率 R(s)s2+25os+02 Damping ratio R(s) C(s) 阻尼比 s(3+20.) D(s)=s2+250ns+o=0 R2=-50n±onV52-1 R=-8±aPi Img. 51 P=-0 临界阻尼(Critically damped):G=l 过阻尼(Overdamped):G>l Real R=-9±jm-g 无阻尼(undamped):=O 负阻尼*：S<0 月，=±j0 School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 6

2015/10/21 6 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 二阶（2 nd order）系统--实例 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 2 2 2 ( ) ( ) 2      n n n C s R s s s 2 2 ( ) 2 0 D s s sn n       1 2 P1、2  n n   2 1,2 1 P j        n n P1,2  n 2 1,2 1 P n n        P j 1,2   n 欠阻尼(Underdamped): 01 无阻尼(undamped):=0 负阻尼*：<0 Undamped natural frequency 无阻尼自然频率 Damping ratio 阻尼比 二阶系统的模型表达

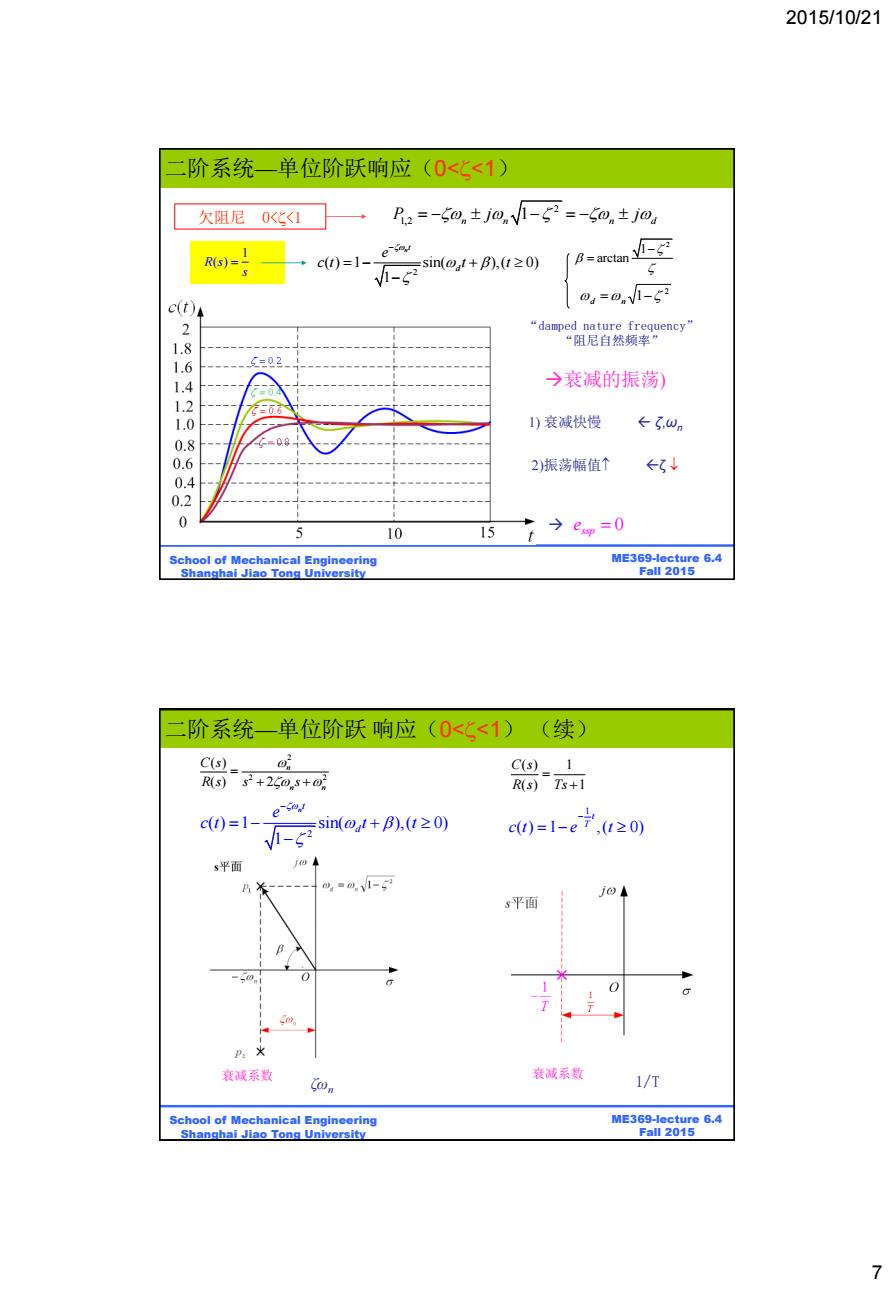
2015/10/21 阶系统一单位阶跃响应(0<<1) 欠阻尼0<C<1 B2=-50n±j0.V1-52=-5@n±jo e R(s)= c(t0=1- sin(@+B),(t20) B-arctan V-2 5 0g=0nV-52 c(t) "damped nature frequency" 286 “阻尼自然频率” 6=02 →衰减的振荡) 420 1)衰减快慢 ←g,wn 8 品Q8 0.6 2)振荡幅值个 ←？↓ 4 02 10 15 →ep=0 School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 阶系统一单位阶跃响应(0<<1) (续) C(s) 回n C(s) 1 R(s) s2+250w5+可 R(s)Ts+1 e-soy c(t)=1- =sin(oal+B),(t≥0) cu)=1-eT,(1≥0 s平面 j B米----- m=m,1- j@4 s平面 P.X 衰减系数 衰减系数 Con 1/T School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 7

2015/10/21 7 ME369-lecture 6.4 Fall 2015 二阶系统—单位阶跃响应（0<<1） School of Mechanical Engineering Shanghai Jiao Tong University 欠阻尼 0<<1 2 1,2 1 P j j             n n n d 2 d n 1 “damped nature frequency” “阻尼自然频率” 1 R s( ) s  2 1 arctan      衰减的振荡) 0 ssp e  2)振荡幅值 1) 衰减快慢  2 ( ) 1 sin( ),( 0) 1 n t d e c t t t            ζ,ωn ζ  ME369-lecture 6.4 Fall 2015 二阶系统—单位阶跃 响应（0<<1） （续） School of Mechanical Engineering Shanghai Jiao Tong University ζωn 1 ( ) 1 ,( 0) t T c t e t     1/T 2 ( ) 1 sin( ),( 0) 1 n t d e c t t t           2 2 2 ( ) ( ) 2 n n n C s R s s s       ( ) 1 ( ) 1 C s R s Ts   衰减系数 衰减系数

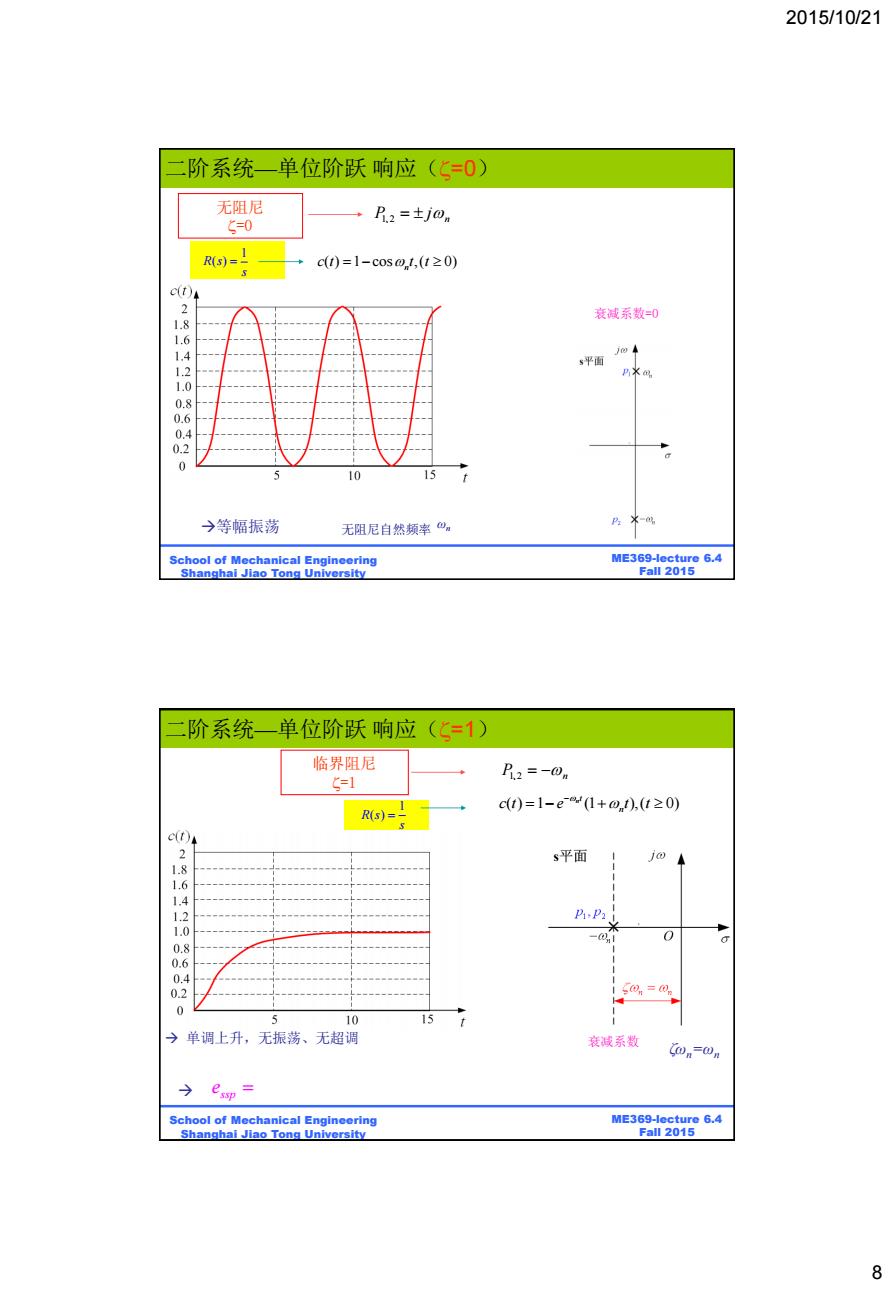
2015/10/21 阶系统一单位阶跃响应(《=0) 无阻尼 R.2=±j0n G=0 =} c(t)=1-cos01,(t≥0) c(t) 衰减系数=0 1 1.6 20 s平面 8 0.4 0.2 0 5 10 15 →等幅振荡 无阻尼自然频率m School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 阶系统一单位阶跃响应(=1) 临界阻尼 51 2=-0m ct)=1-e(1+o),(t≥0) R)=5 c(t) s平面 jo 1.6 1.4 1.2 PiP2 1.0 0 8 0.6 .4 0.2 50,=0m 0 5 10 15 单调上升，无振荡、无超调 衰减系数 Con=On y = School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 8

2015/10/21 8 ME369-lecture 6.4 Fall 2015 二阶系统—单位阶跃 响应（=0） School of Mechanical Engineering Shanghai Jiao Tong University 无阻尼 =0 、 n P1 2   j ωn 1 R s( ) s  ( ) 1 cos ,( 0) n c t t t     等幅振荡 衰减系数=0 无阻尼自然频率 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 临界阻尼 =1 P1、2  n ( ) 1 (1 ),( 0) n t n c t e t t         单调上升，无振荡、无超调 1 R s( ) s  ssp  e  ζωn=ωn 衰减系数 二阶系统—单位阶跃 响应（=1）

2015/10/21 二阶系统一单位阶跃响应(>1) 过阻尼 >1 2=-50±0.V2-1 1 R)-方 c(t)=1- o-(5-oy 22-1(6-2-1 -e-isnPil 22-1G5+2- c(t) 1.8 ≈1-e6-Faw,≥0) 1.6 1.4 s平面 0.8 0.6 0.4 0.2 ,-v-1 -+1 0 0 10 15 →单调上升，无振荡，过渡时间长 15-战V5-1 School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 阶系统一单位阶跃响应（飞<0） 负阻尼 R2=-50.±0.VF2-i 0 极点实部大于零 c(1) -1KK0 K-1 振荡发散 单调发散 School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 9

2015/10/21 9 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 过阻尼 >1 1 2 P1、2  n n   单调上升，无振荡，过渡时间长 2 ( 1) 2 2 1 ( ) 1 2 1( 1) n t c t e               2 ( 1) 1 ,( 0) n t e t          1 R s( ) s  2 ( 1) 2 2 1 2 1( 1) n t e               二阶系统—单位阶跃 响应（>1） ssp e  ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University <0 负阻尼 ζ<0 -1<ζ<0 极点实部大于零 ζ< -1 振荡发散 单调发散 1 2 P1、2  n n   1 R s( ) s  二阶系统—单位阶跃 响应（<0）

2015/10/21 阶系统一单位阶跃响应（汇总） Step Response 6=0 ∠=0.25 =0.5 =0.7 .0 Tme(sec) School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 阶系统一单位脉冲响应（汇总） mpulse Response R(S)=1 5=0 =025 0.6 0<g1 =05 c(t)= V1-52 02 5=0 =0. -02 c(t)=0 sinot 04 =20 5=1 c(1)=@'te- o1 c(1)= （e6-Fjew-e6WFio) 2V52-1 School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 10

2015/10/21 10 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 二阶系统—单位阶跃 响应（汇总） ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University >1 0<<1 =0 c t e t d n t n     sin 1 ( ) 2    c t t n n ( )  sin t n n c t te     2 ( ) ( ) 2 1 ( ) ( 1) ( 1) 2 2 2 n t t n n c t e e                  R s( ) 1  =1 二阶系统—单位脉冲 响应（汇总）