
2015/11/14 ME369-系统模型、分析与控制 7.1频率特性定义 School of Mechanical Engineering ME369-lecture 7.1 Shanghai Jiao Tong University Fall 2015 引例 u,(1)=U sinat R 以) C u.(1) Uo(s)=1+Ts U,(s) ()= 零初始条件 T=RC G(s)= U.(s)_1 U,(s)1+Ts School of Mechanical Engineering Me369-Lecture 7.1 Shanghai Jiao Tong University Fal12015 1
2015/11/14 1 Me369-Lecture 7.1 Fall 2015 School of Mechanical Engineering ME369-lecture 7.1 Shanghai Jiao Tong University 7.1 频率特性定义 ME369-系统模型、分析与控制 Me369-Lecture 7.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 引例 ( ) 1 ( ) ( ) 1 o i U s G s U s Ts T RC 零初始条件 u t U t i m ( ) sin 0 1 ( ) ( ) 1 U s U s i Ts 0 u t( )

2015/11/14 频率响应定义 正弦信号作用下,系统输入量的频率由0→时,稳态输出量与输 入量的幅值比和相位比(复数比)的变化规律。 X(s) G(s) X(s) t→00 x,(t)=msin(oi) x(1)=A(@)x sin[ot+o(o)] School of Mechanical Engineering Me369-Lecture 7.1 Shanghai Jiao Tong University Fall 2015 频率响应定义(续) jv F(@)=A()e() (w) G(jo) A(@) =U(@)+jV(@) p(a) 0 U(@) 幅频特性(幅频) A(@)=lF(@)k=/U(o)+V-(o) V(@) 相频特性(相频) )-LF)-arctanl) 实频特性(实频) U(@)=A(@)cos(@) 虚频特性(虚频) V(@)=A(@)sino(o) School of Mechanical Engineering Me369-Lecture 7.1 Shanghai Jiao Tong University Fall 2015 2
2015/11/14 2 Me369-Lecture 7.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 频率响应定义 正弦信号作用下,系统输入量的频率由0 时,稳态输出量与输 入量的幅值比和相位比(复数比)的变化规律。 ( ) sin( ) r rm x t x t ( ) ( ) sin[ ( )] c rm x t A x t t Me369-Lecture 7.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 幅频特性( 幅频) 相频特性(相频) U jV ( ) ( ) 2 2 A F U V ( ) | ( ) | ( ) ( ) ( ) ( ) ( ) arctan[ ] ( ) V F U U A ( ) ( )cos ( ) V A ( ) ( )sin ( ) ( ) ( ) ( ) j F A e 实频特性(实频) 虚频特性(虚频) 频率响应定义(续)

2015/11/14 频率响应求取 按定义获取 (模型中)输入正弦信号,得到稳态响应 实物中)输入正弦信号,得到稳态响应 直接由传递函数获取(对于线性时不变系统) F(@)=G(j)=G(s)Is=jw Differential equation S= dt 徽分方程 G(s) Transfer function System 传递西数 系统 Frequency characteristics 频率特性 GG®) School of Mechanical Engineering Me369-Lecture 7.1 Shanghai Jiao Tong University Fall 2015 频率特性的求取一传递函数法 G(s)=P(s) p(s) 设不同的实极点 q(s) (+s)(s+S2).(s+Sn) x(t)=Asin ot X(s)=G(s)- Ao _=P(s)Ao 2+o2q5s2+02 ā++++B s+j@s-jo s+ss+S2 s+S x(t)=ae-io +aelo+be+be+be (t≥0) School of Mechanical Engineering Me369-Lecture 7.1 Shanghai Jiao Tong University Fall 2015 3
2015/11/14 3 Me369-Lecture 7.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ----按定义获取 ---(模型中)输入正弦信号, 得到稳态响应 --- 实物中)输入正弦信号, 得到稳态响应 ---- 直接由传递函数获取(对于线性时不变系统) Differential equation 微分方程 System 系统 Frequency characteristics 频率特性 Transfer function 传递函数 F()= G(j )=G(s)|s=jω 频率响应求取 Me369-Lecture 7.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 频率特性的求取—传递函数法 x t A t r ( ) sin 1 2 ( ) ( ) ( ) ( ) ( )( )...( ) n p s p s G s q s s s s s s s 2 2 2 2 ( ) ( ) ( ) ( ) c A p s A X s G s s q s s 1 2 1 2 1 ( ) ... n j t j t s t s t s t c x t ae ae b e b e b e ( 0) t 1 2 1 2 ... n n a a b b b s j s j s s s s s s 设不同的实极点
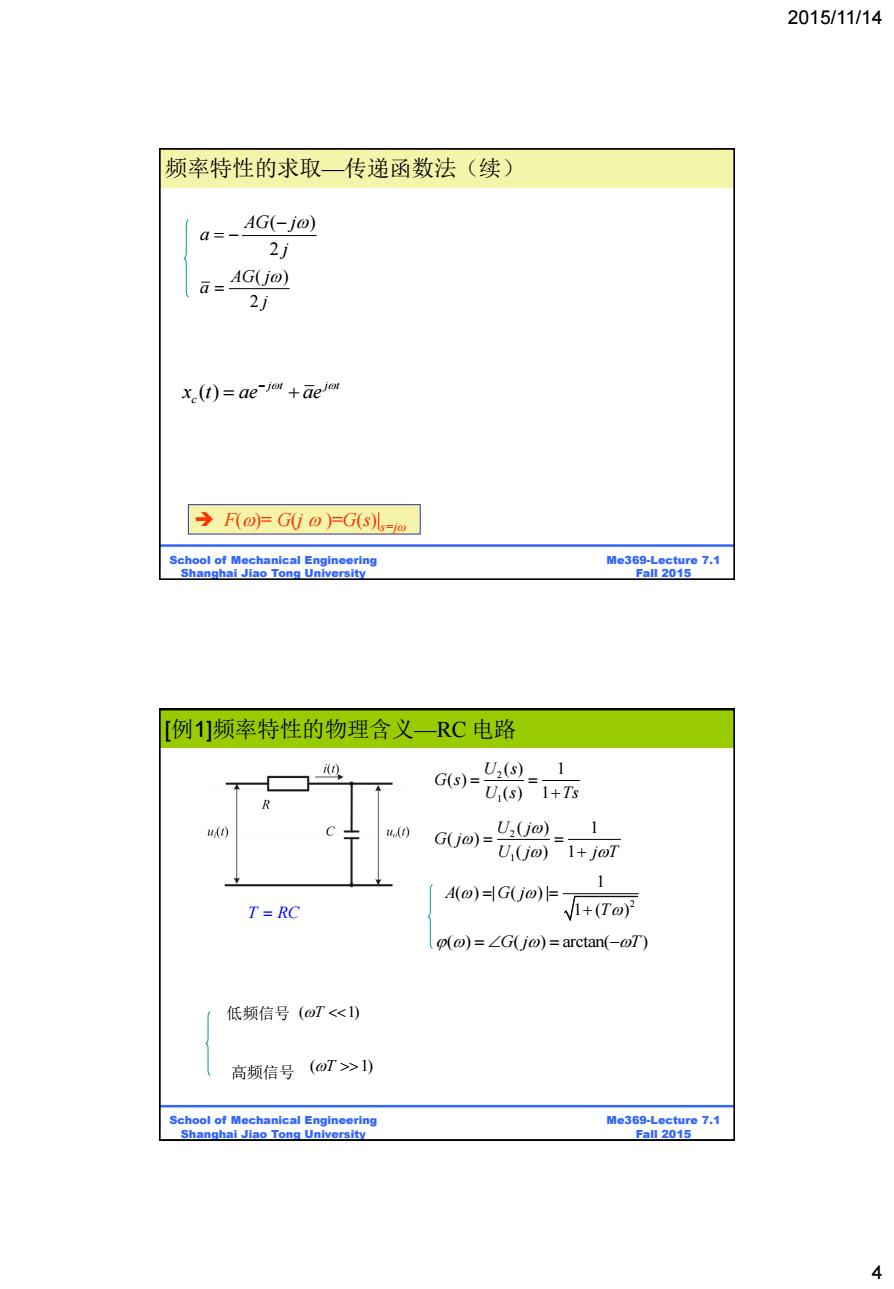
2015/11/14 频率特性的求取一传递函数法(续) a- AG(-j@) 2j Q= AG(j@) 2j X(t)=ae-jo+aelou →F0=G(j@=G(sL=0 School of Mechanical Engineering Me369-Lecture 7.1 Shanghai Jiao Tong University Fall 2015 [例1]频率特性的物理含义一RC电路 i) G(s)= U2(s)1 U (s)1+Ts () U,(jo) 1 G(io)= U(jo)1+joT A(@)=G(j@)= 1 T=RC V+(ToY o(@)=LG(j@)=arctan(-@T) 低频信号(oT1) School of Mechanical Engineering Me369-Lecture 7.1 Shanghai Jiao Tong University Fall 2015 4
2015/11/14 4 Me369-Lecture 7.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) j t j t c x t ae ae ( ) 2 AG j a j ( ) 2 AG j a j F()= G(j )=G(s)|s=jω 频率特性的求取—传递函数法(续) Me369-Lecture 7.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1]频率特性的物理含义—RC 电路 2 1 ( ) 1 ( ) ( ) 1 U s G s U s Ts T RC 2 1 ( ) 1 ( ) ( ) 1 U j G j U j j T 2 1 ( ) | ( ) | 1 ( ) A G j T ( ) ( ) arctan( ) G j T ( 1) T ( 1) T 低频信号 高频信号

2015/11/14 [例2-1]吸振一不含吸振环节 M M,=10kg K1=1000N/mB=4N/m/s) G)=▣ 1 0.1 F(s)Ms2+Bs+K1s2+0.4s+100 FWw 4 10 带棉 Me369-Lecture 7.1 Fall 2015 [例2-2]吸振一含吸振环节 M,=10kg K,=1000N/m B=4Nm/s) M,=1kg K2=100N/m B,=0.1N/m/s) G(s)= X(s) s2+0.1s+100 F(S)10s+5.1s3+2100.452+500s+100000 ∽whw阳 00 00@ School of Mechanical Engineering Me369-Lecture 7.1 Shanghai Jiao Tong University Fall 2015 5
2015/11/14 5 Me369-Lecture 7.1 Fall 2015 [例2-1]吸振—不含吸振环节 1 2 2 1 1 1 ( ) 1 0.1 ( ) ( ) 0.4 100 X s G s F s M s B s K s s ft() B1 K1 M1 1 x 1 M kg 10 1 K N m 1000 / 1 B N m s 4 /( / ) Me369-Lecture 7.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例2-2]吸振—含吸振环节 B2 ft() B1 K1 K2 M1 M2 2 x 1 x 2 M kg 1 2 K N m 100 / 2 B N m s 0.1 /( / ) 1 M kg 10 1 K N m 1000 / 1 B N m s 4 /( / ) 2 1 4 3 2 ( ) 0.1 100 ( ) ( ) 10 5.1 2100.4 500 100000 X s s s G s F s s s s s

2015/11/14 [例2-3]吸振器加入前后对比 [前] [后] School of Mechanical Engineering Me369-Lecture 7.1 Shanghai Jiao Tong University Fall 2015 6
2015/11/14 6 Me369-Lecture 7.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例2-3]吸振器加入前后对比 [前] [后]