
ME369-系统模型、分析与控制 4.2方块图 School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 方块图定义 Desired value Actual value 结构方块图 设定值输入量 Controller Plant 实际值输出量 (Construction 控制对象 修 控制器 Block diagram) Feedback value measurer 反馈值 测量元件 依据信号的流向,将各元件的方块连接起来的图形化表达 R(s) E(s) C(s) G(s) 函数方块图 (Function Block diagram) B(s) H(s) School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 1
1 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 4.2 方块图 ME 369– 系统模型、分析与控制 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 结构方块图 (Construction Block diagram) 依据信号的流向 ,将各元件的方块连接起来的图形化表达 方块图定义 Desired value 设定值/输入量 Controller 控制器 Plant 控制对象 measurer 测量元件 Actual value 实际值/输出量 Feedback value 反馈值 函数方块图 (Function Block diagram)
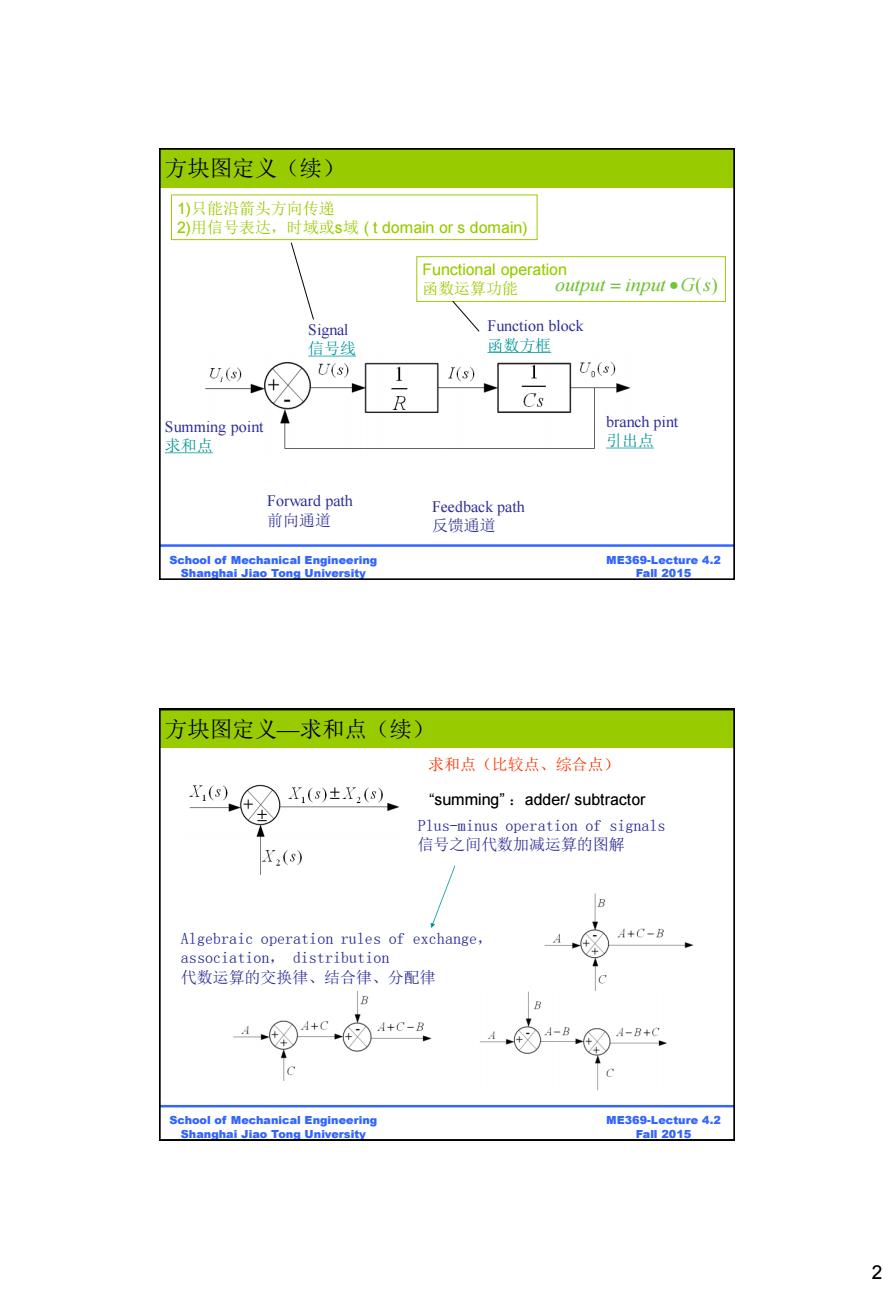
方块图定义(续) 1)只能沿箭头方向传递 2)用信号表达,时域或s域(t domain or s domain) Functional operation 函数运算功能 output inputG(s) Signal Function block 信号线 函数方框 U,(s) U(s) I(s) U(s) Summing point branch pint 求和点 引出点 Forward path Feedback path 前向通道 反馈通道 School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 方块图定义一求和点(续) 求和点(比较点、综合点) X(s) X1(s)±X,(s) "summing":adder/subtractor Plus-minus operation of signals 信号之间代数加减运算的图解 X,(s) Algebraic operation rules of exchange, A+C-8 association,distribution 代数运算的交换律、结合律、分配律 B A+C-B 4=B A-B+C School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 2
2 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Summing point 求和点 Function block 函数方框 branch pint 引出点 Signal 信号线 1)只能沿箭头方向传递 2)用信号表达,时域或s域 ( t domain or s domain) Functional operation 函数运算功能 output input G s ( ) Forward path 前向通道 Feedback path 反馈通道 方块图定义(续) ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 求和点(比较点、综合点) Plus-minus operation of signals 信号之间代数加减运算的图解 Algebraic operation rules of exchange, association, distribution 代数运算的交换律、结合律、分配律 “summing” :adder/ subtractor 方块图定义—求和点(续)

[例1]绘制方块图 u Ri+uo %=油 LT U,(s)=RI(s)+U(s) U.s)=11s) Cs School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 例2]绘制方块图 ●● dx0=f0-f。-f 1 M X(s)=- d F()5()-F( 方=B「4@_40l F(s)=Bs[X (s)-X(s)] dt」 LT f人=K[x0-x E(5)=K[X(s)-X2(s)] M. (D=f+fe-f 1 X,(s)= dr 5(+5()-5 Ik:=K2x2(t) Fk,(s)=K2X2(s) School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 3
3 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1]绘制方块图 i 0 u Ri u 0 1 u i t d C LT ( ) ( ) ( ) U s RI s U s i o 1 ( ) ( ) c I s U s C s ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 2 1 1 2 ( ) ( ) B K d x t M f t f f dt 1 2 ( ) ( ) B dx t dx t f B dt dt 1 1 1 2 ( ) ( ) K f K x t x t 1 2 2 2 2 2 ( ) B K K d x t M f f f dt 2 2 2 ( ) K f K x t 1 1 2 1 1 ( ) [ ( ) ( ) ( )] X s F s F s F s B K M s 1 2 ( ) [ ( ) ( )] F s Bs X s X s B 1 1 1 2 ( ) [ ( ) ( )] F s K X s X s K 1 2 2 2 2 1 ( ) [ ( ) ( ) ( )] X s F s F s F s B K K M s 2 2 2 ( ) ( ) F s K X s K LT [例2]绘制方块图
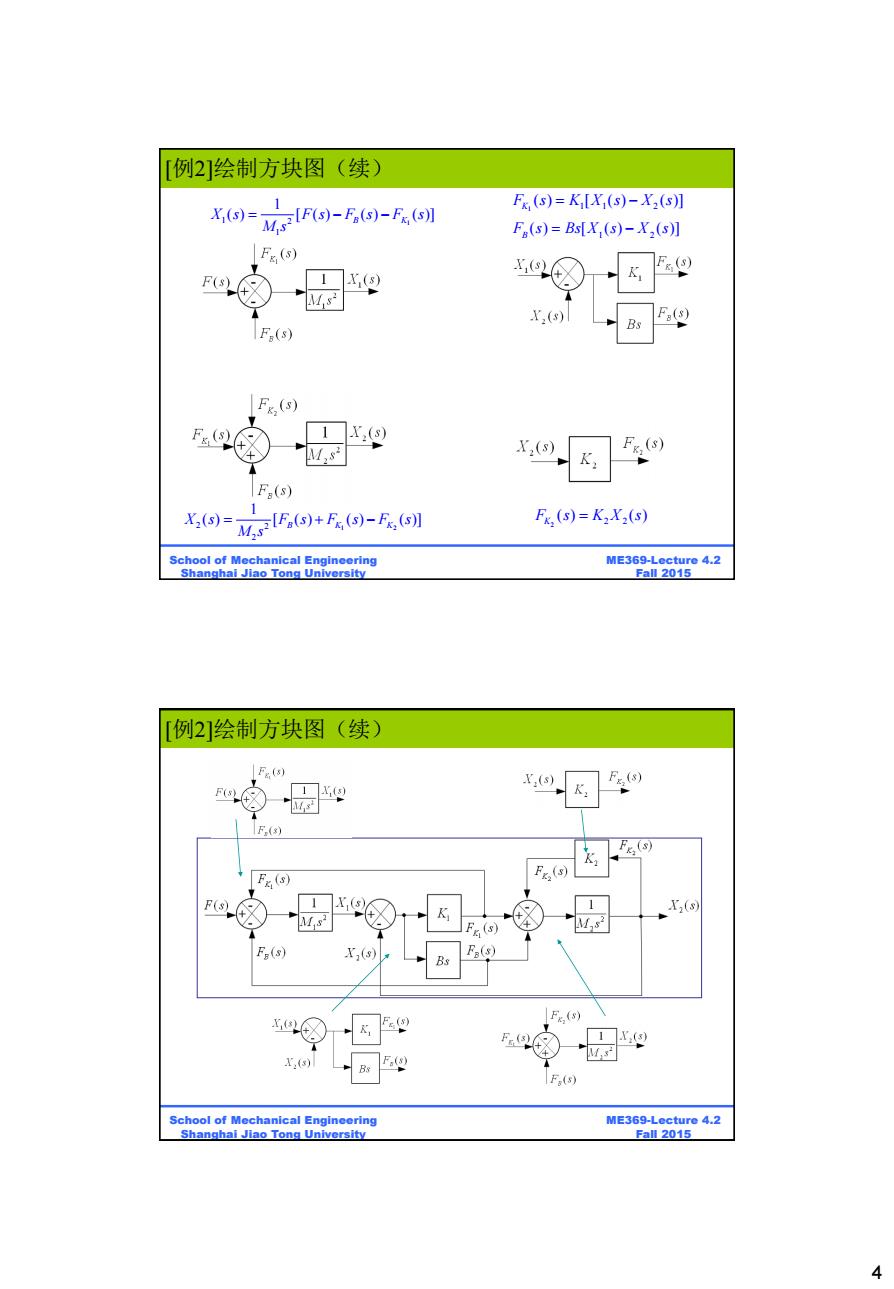
[例2]绘制方块图(续) X(S)= MF)-F)-Fs】 F(S)=K[X(s)-X(S】 F(S)=Bs[X(s)-X,(S】 Fg(s) 1X(s) K X,(s) Bs r.e F(s) Fx(s) Fs(s) M,s- X,(s) F(s) X2(S)= ()+5(-5() 1 F,(s)=K2X2(S) School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 例2]绘制方块图(续) F(3) □型 xK F() Fe (s) Fx (s) F,(9 ( Er(s) F(s) X;(s) F(s) Bs F,() F 口g Bs F.( M F:(s) School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 4
4 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 1 2 1 1 ( ) [ ( ) ( ) ( )] X s F s F s F s B K M s 1 2 ( ) [ ( ) ( )] F s Bs X s X s B 1 1 1 2 ( ) [ ( ) ( )] F s K X s X s K 1 2 2 2 2 1 ( ) [ ( ) ( ) ( )] X s F s F s F s B K K M s 2 2 2 ( ) ( ) F s K X s K [例2]绘制方块图(续) ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例2]绘制方块图(续)

[例3]绘制方块图 i 4 C u,0-4@=i0 U,(s)-U,(5)=I(s) R R 40-2c0-0池 LT )=4- Cs 4①-.@=i,(0 Us)-U@=1,s) R E ()-fi(d 0 U(s)=- School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 例3]绘制方块图(续) U,(s)-U(s) U(s)-U.(s =1,(s) R =1s) R Us=4-s) U.=40 Cs Cs School of Mechanical Engineering ME369-Lecture 4.2 Shanghal Jiao Tong University Fall 2015 5
5 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 1 1 ( ) ( ) ( ) r u t u t i t R 1 1 2 1 1 u t i t i t t ( ) [ ( ) ( )]d C 1 2 2 ( ) ( ) ( ) c u t u t i t R 2 2 1 ( ) ( )d c u t i t t C 1 1 1 ( ) ( ) ( ) U s U s r I s R 1 2 1 1 ( ) ( ) ( ) I s I s U s C s 1 2 2 ( ) ( ) ( ) U s U s c I s R 2 2 1 ( ) ( ) U s I s c C s LT [例3]绘制方块图 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 1 1 ( ) ( ) ( ) U s U s r I s R 1 2 1 1 ( ) ( ) ( ) I s I s U s C s 1 2 2 ( ) ( ) ( ) U s U s c I s R 2 2 1 ( ) ( ) U s I s c C s [例3]绘制方块图(续)

方块图获取系统传递函数 -一化简法 方块图运算规则(Algebra rules) 串联、并联、反馈 方框图等效变换法则(Equivalent rules) 基于引出点的简化 基于比较点的简化 方块图化简(reduction) 一公式直接法 -代数法 School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 运算化简一串联 几个环节串联的总传递函数一每环节的传递函数的乘积 X(s) X(s) X.(s) G(s)=G(s)G,(s)G(s)...G(s X.(s) 隔离放大器 School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 6
6 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 方框图等效变换法则(Equivalent rules) ---公式直接法 --- 化简法 ---代数法 方块图化简(reduction) 方块图运算规则(Algebra rules) 串联、并联、反馈 基于比较点的简化 基于引出点的简化 方块图获取系统传递函数 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 几个环节串联的总传递函数==每环节的传递函数的乘积 运算化简—串联
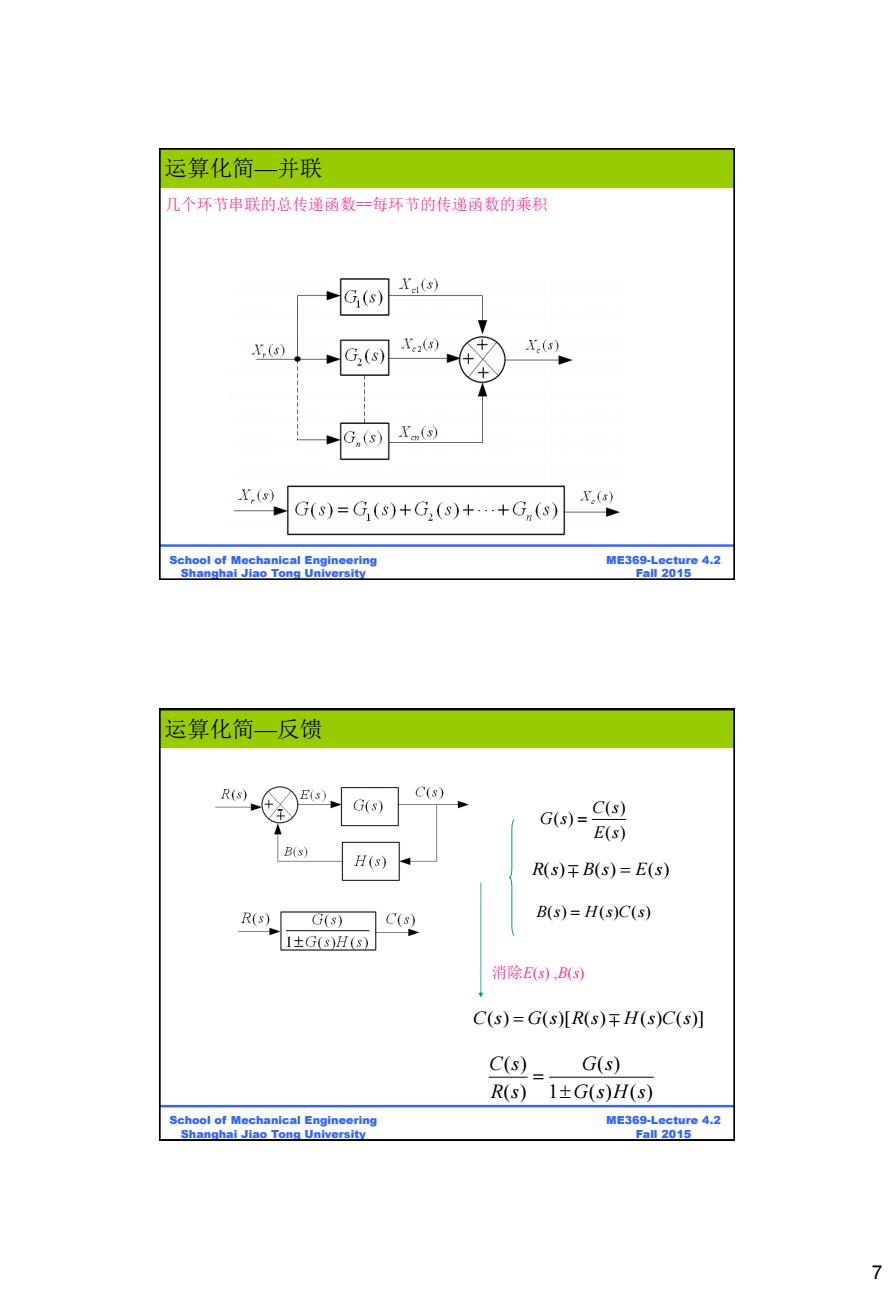
运算化简一并联 几个环节串联的总传递函数一每环节的传递函数的乘积 Xa(s) G1() X,(s) X2(5) X.(s) G(s) G,(s) X(s) X,(s) X.(s) G(s)=G(s)+G,(s)+…+G(s) School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 运算化简一反馈 R(s) (s) C(s) G(s) C(s) G(s)= E(s) B(s) H(s) R(S)干B(s)=E(S) R(s) G(s) C(s) B(s)=H(s)C(s) 1±G(s)H(s) 消除E(s),B(s) C(s)=G(s)[R(s)H(s)C(s)] C(s) G(s) R(s)1±G(s)H(s) School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 7
7 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 几个环节串联的总传递函数==每环节的传递函数的乘积 运算化简—并联 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) ( ) ( ) C s G s E s R s B s E s ( ) ( ) ( ) B s H s C s ( ) ( ) ( ) 消除E(s) ,B(s) C s G s R s H s C s ( ) ( )[ ( ) ( ) ( )] ( ) ( ) ( ) 1 ( ) ( ) C s G s R s G s H s 运算化简—反馈
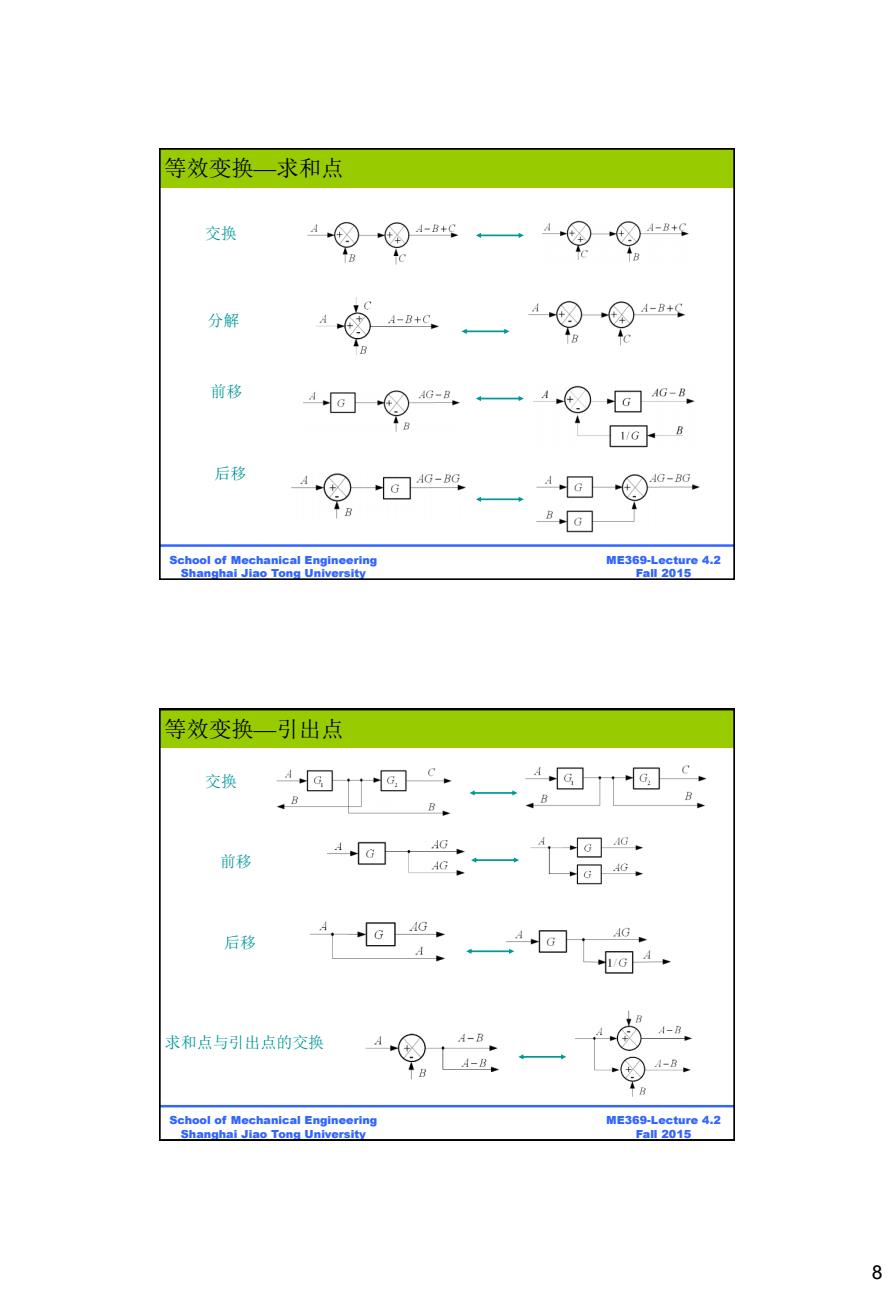
等效变换一求和点 交换 分解 前移 后移 School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fa12015 等效变换一引出点 交换 4G 、B B B AG 前移 后移 回 AG 求和点与引出点的交换 A-B ⑧ A-B ↑B School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 8
8 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 前移 后移 交换 分解 等效变换—求和点 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 交换 求和点与引出点的交换 前移 后移 等效变换—引出点
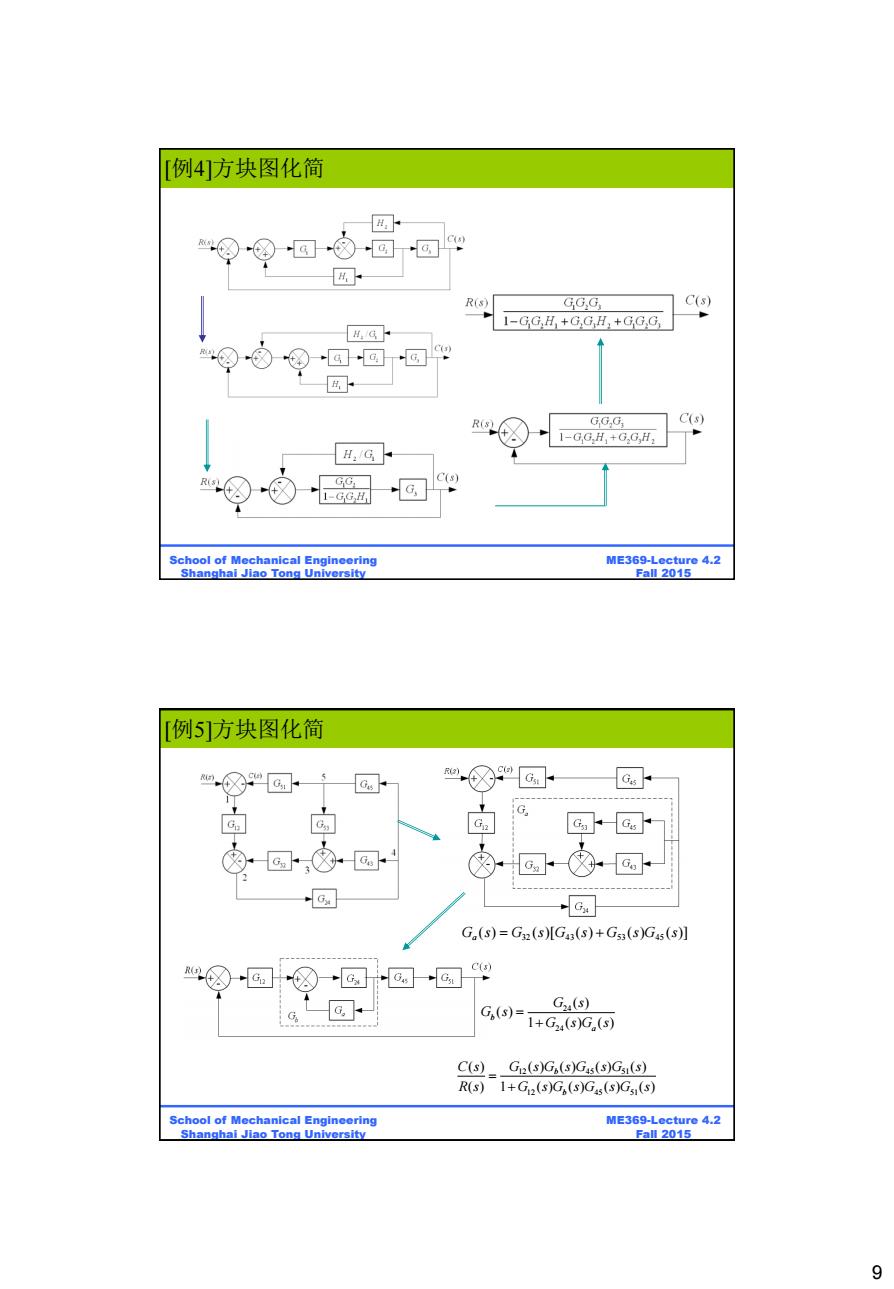
[例4]方块图化简 品 R(s) GG.G, C(s) 1-GG,H+G,G H,+GGG H,G← GG,G, C(s) 1-GG,H,+G,G H, H:/G GG☐ C(8) 1-GG School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fa12015 例5]方块图化简 68ma✉; -8 Gus ☆ 卤 卤 G GGe ②@四②团 ②四⑧四 8 G(s)=Gz(s)[G4,(s)+G53(s)G45(s】 c(s) G(s) G G,(9= 1+G24(s)G(s) C(s)_Gp(s)G,(s)Gas(s)Gs(s) R(s)1+G2(s)G,(s)Gxs(s)Gs(s) School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 9
9 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [Reduction method 例4]方块图化简–example (1) ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 32 43 53 45 ( ) ( )[ ( ) ( ) ( )] G s G s G s G s G s a 24 24 ( ) ( ) 1 ( ) ( ) b a G s G s G s G s 12 45 51 12 45 51 ( ) ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) b b C s G s G s G s G s R s G s G s G s G s [例5]方块图化简

[例6]方块图化简 a 历 H ME369-Lecture 4.2 Fall 2015 直接公式法 格极公式(Mason's formula): 只有一条前向通道的多回路系统的闭环传递函数 前向通道传递函数:输入量到输出量间的串联环节的总传递函数 Φ(S)= G(S) n V+ (±)Ga(S) i=l 各交错反馈或多环局部反馈的开环传递函数 反馈回路的总数 +负反馈 一正反馈 School of Mechanical Engineering ME369-Lecture 4.2 Shanghai Jiao Tong University Fall 2015 10
10 ME369-Lecture 4.2 Fall 2015 [例6]方块图化简 ME369-Lecture 4.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 直接公式法 1 ( ) ( ( ) 1 ( ) ) n A Bi i G s s G s 前向通道传递函数:输入量到输出量间的串联环节的总传递函数 反馈回路的总数 各交错反馈或多环局部反馈的开环传递函数 + 负反馈 - 正反馈 梅逊公式(Mason’s formula): 只有一条前向通道的多回路系统的闭环传递函数