ME369-系统模型、分折与控制 3.2拉普拉氏变换求解微分方程 →拉普拉氏求解系统时域响应 *线性时不变微分方程 (linear,time-invariant differential equation) School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 LT法求解常微分方程 +初始条件(Initial condition,IC) 时域模型 频域模型 (时间自变量的微分方程) (s自变量的代数方程) 代数求解 (algebra) 微积分求解 (calculus) 频域解Y(s) ILT 时域解y(⑨ School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 1
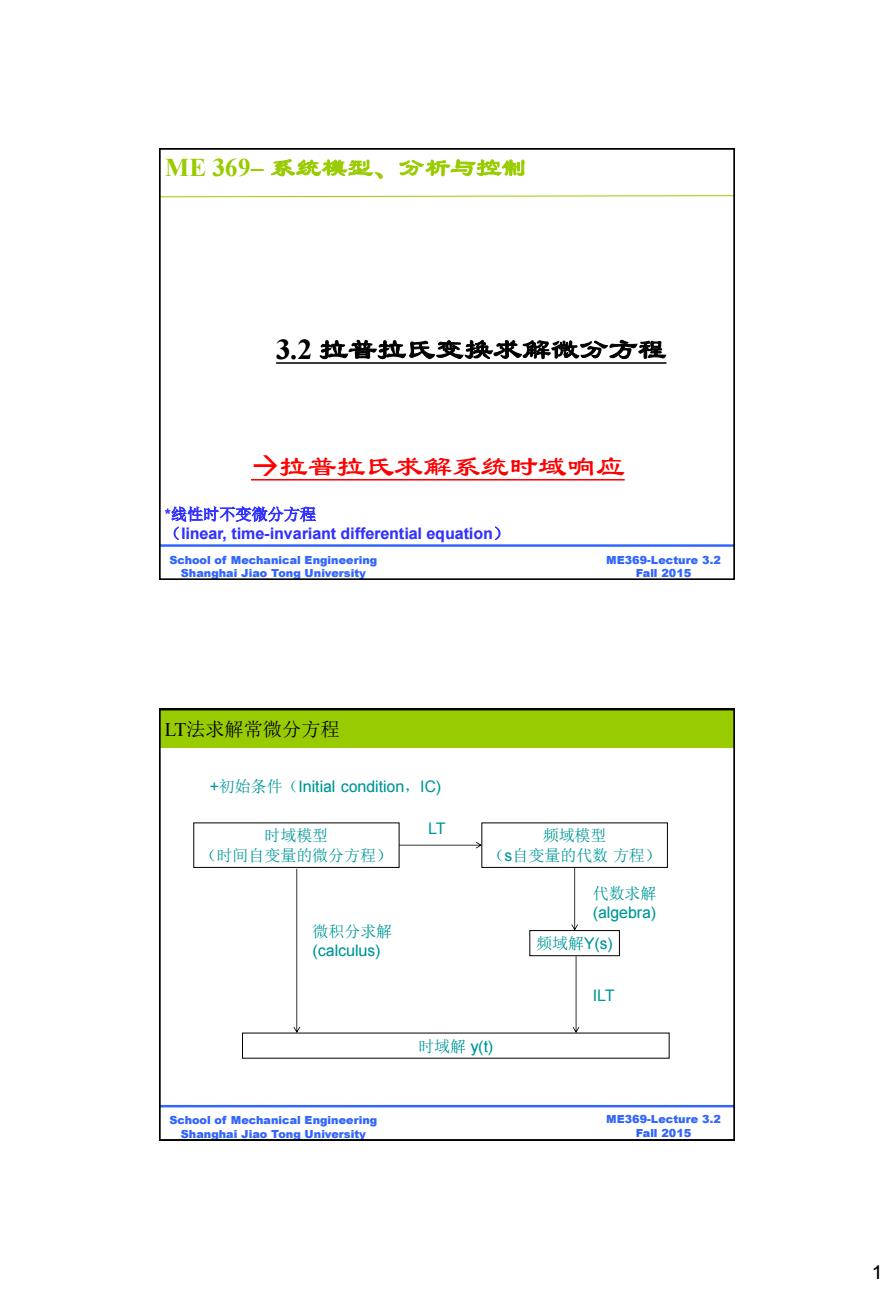
1 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 3.2 拉普拉氏变换求解微分方程 *线性时不变微分方程 (linear, time-invariant differential equation) 拉普拉氏求解系统时域响应 ME 369– 系统模型、分析与控制 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University LT法求解常微分方程 +初始条件(Initial condition,IC) 时域模型 (时间自变量的微分方程) 频域模型 (s自变量的代数 方程) 频域解Y(s) 代数求解 (algebra) 微积分求解 (calculus) ILT LT 时域解 y(t)

[例) 4x+y=10 x(0)=0 求 x(t) 已知 -x+3y+2y=0 y(0)=5 y(t) School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 阶系统(First order system)的自由响应(free response) tr+x=0,x(0)= School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 2
2 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1] 4 10 3 2 0 x y x y y (0) 0 (0) 5 x y () () xt yt , 已知 求 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 一阶系统(First order system)的自由响应(free response) 0 x x x x 0, (0)

阶系统的阶跃响应(step response) tx+x=K,x(0)=Xp School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 阶系统(Sencond order system)的自由响应((free response) +6x+25x=0,x(0)=1,(0)=-3 School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 3
3 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 0 x x K x x , (0) 一阶系统的阶跃响应(step response) BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University x x x x x 6 25 0, (0) 1, (0) 3 二阶系统(Sencond order system)的自由响应(free response)

阶系统的阶跃响应 二 求+6x+25x=1+25u,x(0)=1,x(0)=-3 School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 阶系统的阶跃响应(续) School of Mechanical Engineering ME369-Lecture 3.2 Shanghai Jiao Tong University Fall 2015 4
4 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University x x x u u x x 6 25 25 , (0) 1, (0) 3 二阶系统的阶跃响应 BE315-Lecture 3.3 Fall 2011 ME369 Lecture 3.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 二阶系统的阶跃响应(续)