
ME369-系统模型、分析与控制 2.1平动机械系统建桃 School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 变量 x:位移[m] x=v v:速度 [m/sec] i=求=a a:加速度 [m/sec2] f力N p=fv=f求=m p: 功率[Nm/sec] w6)=w6,)+pt=w,)+-刘h w:功[Nm、J刀 School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 1
1 BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ME 369– 系统模型、分析与控制 2.1 平动机械系统建模 BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 变量 x v vxa p f v f x w 1 1 0 0 10 0 () () () ( ) t t t t w t w t pdt w t f x dt x: 位移 [m] v: 速度 [m/sec] a: 加速度 [m/sec2] f: 力 [N] p: 功率 [Nm/sec] w: 功 [Nm、J]

模型元件 惯性(Inertia)-质量(mass) +x() +v() f()=m(=mdx( f( dt dr 刚度(Stiffness))-弹簧(spring) 储存动能(Store Kinetic Energy) +x(0 +3(0 f()=K[x()-x2)]=Kx() (0 ·2(0 =K(0-,d=K0)d f(() w f(() 摩擦(Friction)一阻尼器(Damper) 储存势能(Store Potential Energy) +1() 一0 fa()=B[(t)-(t】=Bv(t)) +x1(0 →2(0 =B@_本,凸]=B0 fu(1) fa(r) dt dt dt 耗能(Dissipate Energy School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 理想元件 弹簧 (2-x f=K(x2-x) E,I T Massless No Damping Linear School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015
2 BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 模型元件 惯性(Inertia) --质量(mass) 刚度(Stiffness)--弹簧(spring) 摩擦(Friction)--阻尼器(Damper) 2 2 () () ( ) m dv t d x t ft m m dt dt 1 2 1 2 ( ) [ ( ) ( )] ( ) [ ( ) ( )] ( ) k t t f t K x t x t Kx t K v t v t dt K v t dt 1 2 1 2 ( ) [ ( ) ( )] ( ) () () () [ ] Bf t B v t v t Bv t dx t dx t dx t B B dt dt dt 耗能(Dissipate Energy) 储存势能(Store Potential Energy) 储存动能(Store Kinetic Energy) BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 理想元件-----------弹簧 2 1 ( ) sf Kx x Massless / No Damping / Linear K

理想元件 -----阻尼器 Door Cylinder Air chamher Damping Door adjustmen Door frame attachment screw Pneumatic door closer Orifices Outer cylinder Inner cylinder 气动闭门器 (piston) Air flow during Spring compression Cylinder Piston Piston O-ring rod seal Cylinder Door frame Shock absorber("oleo strut") attachment point 吸振器(“黄油支柱”) School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 元件连接一弹簧串并联(in Series/Parallel) → K K K M X2 →5 KEQ School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 3
3 BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Shock absorber (“oleo strut”) 吸振器(“黄油支柱”) Pneumatic door closer 气动闭门器 理想元件-----------阻尼器 BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 元件连接—弹簧串并联( in Series/ Parallel)
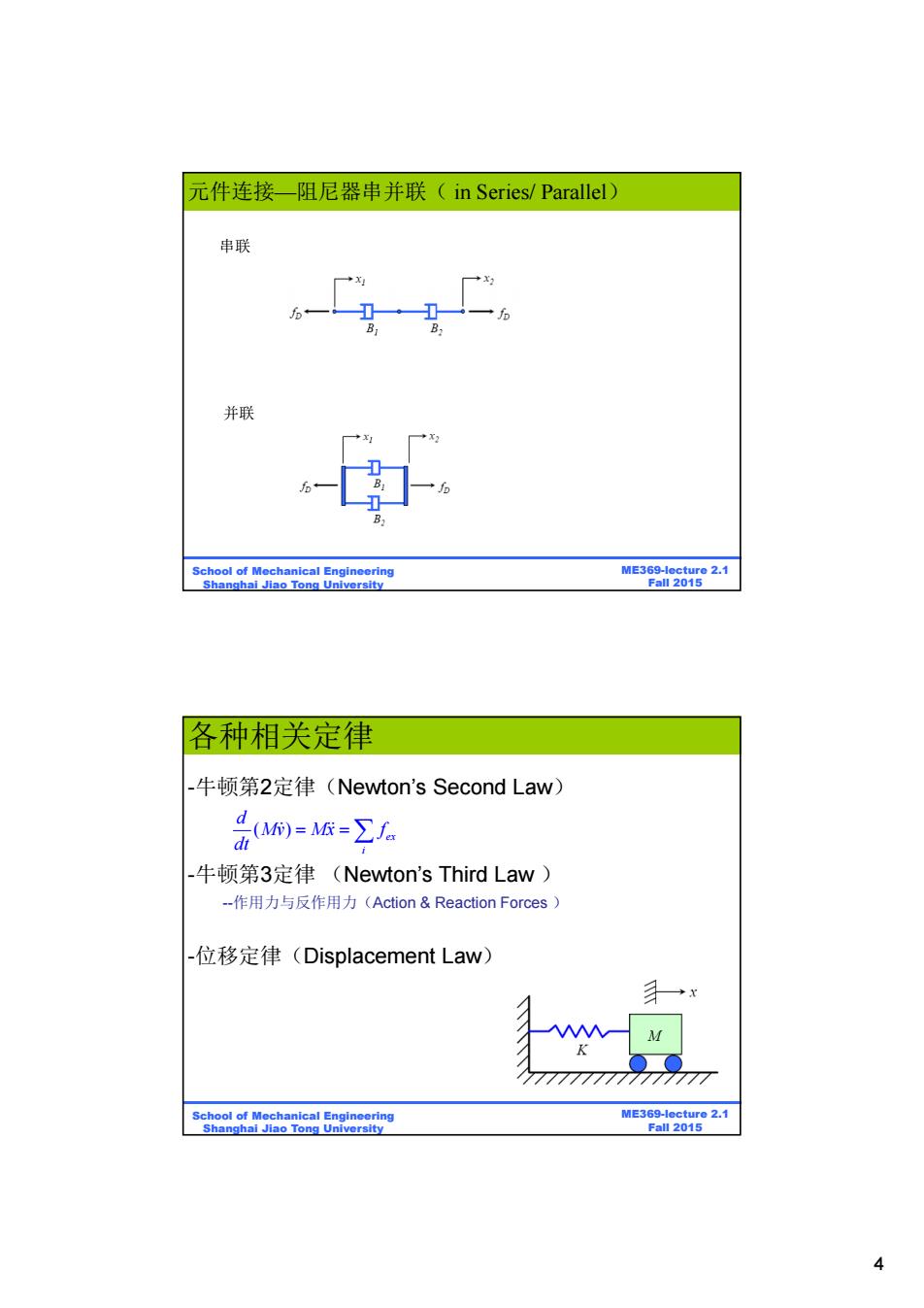
元件连接一阻尼器串并联(in Series/.Parallel) 串联 并联 School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 各种相关定律 _牛顿第2定律(Newton's Second Law) 品陶=A版=∑ 牛顿第3定律(Newton's Third Law) -作用力与反作用力(Action&Reaction Forces) -位移定律(Displacement Law) 手一x M K School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 4
4 BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 串联 并联 元件连接—阻尼器串并联( in Series/ Parallel) BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 各种相关定律 -牛顿第2定律(Newton’s Second Law) ( ) ex i d Mv Mx f dt -牛顿第3定律 (Newton’s Third Law ) --作用力与反作用力(Action & Reaction Forces ) -位移定律(Displacement Law)

建模步骤 [1]理解功能,分析系统,确定输入、输入变量 [2]采用基本元件画出简化图 [3]推导数字模型,如微分方程(diff.Eq.) 一确定参考点和正方向 -为每个基本元件画自由物体受力图(Free-Body-Diagram,FBD) 一列出以基本元件为内部变量的方程 动力学(Kinetics)定律如Newton/.Euler laws 运动学(Kinematics)定律 connection can't break [4取消中间变量,化简方程形式 [5]化成标准形式,得到运动方程(Equation of Motion,EOM) School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 例1] 手一x - M K 77777777777777 School of Mechanical Engineering ME369-lccture 2.1 Shanghai Jiao Tong University Fall 2015 5
5 BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 建模步骤 [1]理解功能,分析系统,确定输入、输入变量 [2] 采用基本元件画出简化图 [3]推导数字模型,如微分方程(diff. Eq.) --确定参考点和正方向 --为每个基本元件画自由物体受力图(Free-Body-Diagram ,FBD) --列出以基本元件为内部变量的方程 动力学(Kinetics)定律 如 Newton/Euler laws 运动学(Kinematics)定律 connection can’t break [4]取消中间变量, 化简方程形式 [5] 化成标准形式, 得到 运动方程(Equation of Motion, EOM) BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1]

[例2] f) m 0 m School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 「例31 ·WWWM m School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 6
6 BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例2] BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例3]

[例4] 人* K · C: C3 School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 静态平衡(static equilibrium) k g 2k S ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 7
7 BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例4] BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 静态平衡(static equilibrium)

[例5] 滑轮(pulley)系统,设滑轮的惯量可以忽略不计,请给出运动方程(EOM) LLL0LE1111110 k23 m k1 s 7717/77711/ School of Mechanical Engineering ME369-lecture 2.1 Shanghai Jiao Tong University Fall 2015 双质量块的1/4车辆模型(Quarter--car model with2mass) M School of Mechanical Engineering ME369-lccture 2.1 Shanghai Jiao Tong University Fall 2015 8
8 BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例5] 滑轮 (pulley)系统, 设滑轮的惯量可以忽略不计,请给出运动方程(EOM) BE315-Lecture 2.1 Fall 2011 ME369-lecture 2.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 双质量块的1/4 车辆模型(Quarter–car model with 2 mass)