上海交通大学：《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[04]Lecture31-LT Definition-in class 拉普拉氏变换——定义及性质

ME369-系统模型、分折与控制 3.1拉普拉氏变换-定义及性质 School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 内容汇总 -拉普拉氏变换(LT)定义 按定义 LT求取 查表 通过LT性质 -拉普拉氏反变换(LD求取 部分分式法 终值定理小议 School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 1

1 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 3.1 拉普拉氏变换 –定义及性质 ME 369– 系统模型、分析与控制 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University --拉普拉氏变换（LT） 定义 --LT 求取 按定义 通过LT性质 查表 --拉普拉氏反变换（ILT)求取 部分分式法 --终值定理小议 内容汇总

拉普拉氏变换(Laplace Transform,LT定义 i,Continue real time function实函数r(): 2.t0,f()=0: s:complex variable 3.20, is convergent in a realm of s 复变量 f(De"dr (在的某一域内收敛) Image funtion 像函数 F(s) f(t)e-sdt Operational symbol of LT 拉普拉氏变换算子 1 Primary function f(t)=L'[F(s)]= F(s)e"ds 原函数 2πjJc-jm Operational symbol of inverse LT 拉普拉氏反变换算子 C:real constant实常数 School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 按定义求取LT -一指数函数(Exponential function) [e]= s+a -三角函数(Sinusoidal function) Lisinon=o Licosor= -单位阶跃函数(Unit Step function) -单位脉冲函数(Unit Impluse function) -幂函数(Power function) School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 2

2 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 拉普拉氏变换（ Laplace Transform， LT) 定义 0 ( ) [ ( )] e d ( )     st F f t t s L f t s: complex variable 复变量 Image funtion 像函数 Primary function 原函数 1.Continue real time function 实函数f(t)； 2.t<0 ， f(t)=0； 3.t0， is convergent in a realm of s (在s的某一域内收敛) 0 ( ) st f t e dt    Operational symbol of LT 拉普拉氏变换算子 1 1 ( ) [ ( )] ( )e d 2 c j c st j f t F s F s s j L          C: real constant 实常数 Operational symbol of inverse LT 拉普拉氏反变换算子 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 按定义求取LT ---指数函数(Exponential function) ---三角函数(Sinusoidal function ) ---幂函数(Power function) ---单位阶跃函数(Unit Step function) ---单位脉冲函数 (Unit Impluse function ) 1 [e ] at L s a    2 2 L t [sin ] s      2 2 [cos ] s L t s    

指数函数的LT Led 1=e s+a School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 三 角函数的LT 4 sin]=人'sinat·ed 。(e-e)e"d s+o sinot jega-egan 1,1-1)= 2j s-jo s+j@'s2+02 cos@t·edt (el)e-"dt coSot J02 s2+o2 s2+o2 School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 3

3 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 1 e at L s a           0 [ ] at at st L e e e dt        指数函数的LT BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 三角函数的LT 0 [ ] sin sin d e st L t   t t     0 1 (e e ) 2 d j t j t st t j e         0 [ ] cos cos d e st L t   t t     2 2 1 1 1 ( ) 2 j s j s j s           0 1 (e e ) d 2 j t j t st e t         1 2 2 L t sin s             2 2 s s    0 0 1 ( e 2 d e d ) j t j t st st j e t e t            1 2 2 cos s L t s           

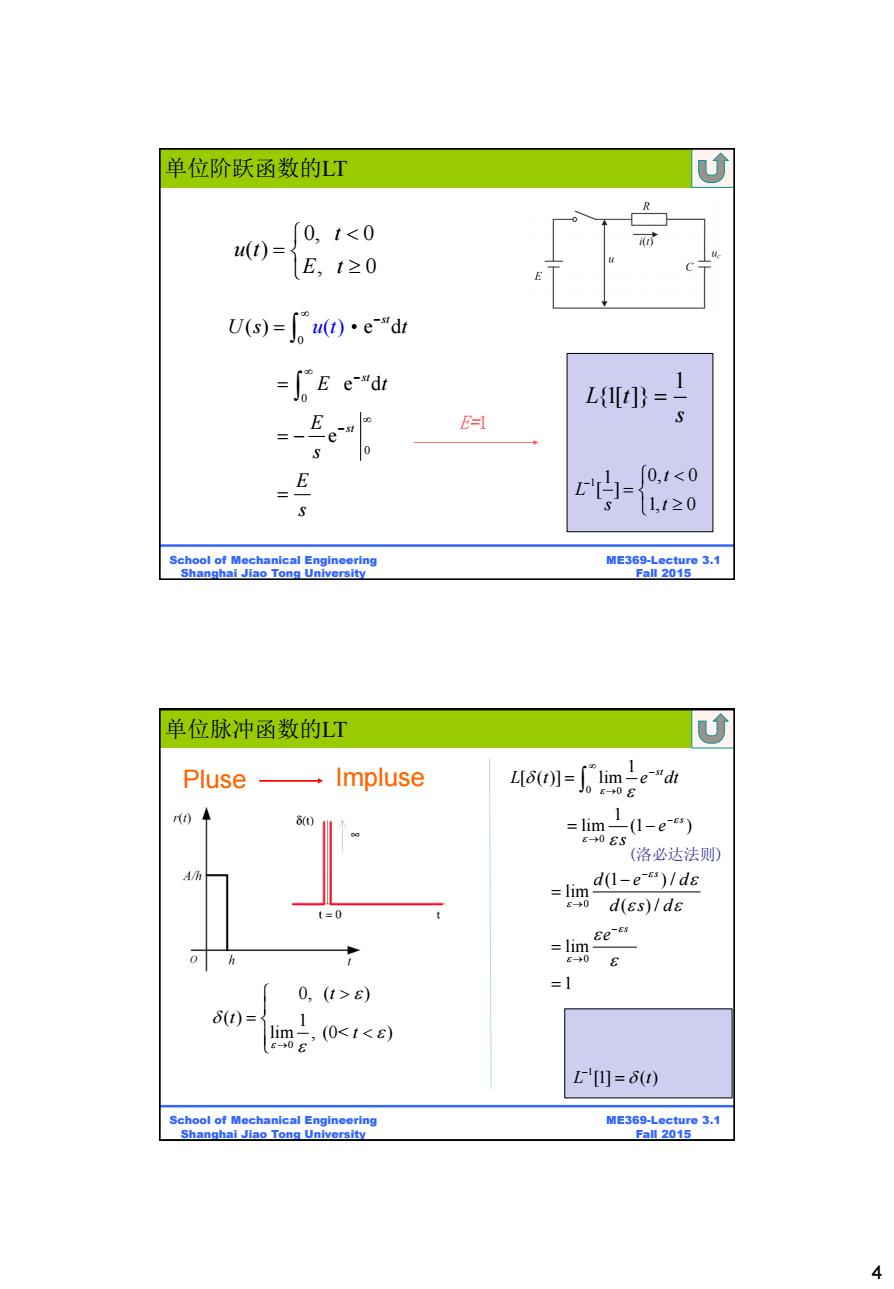
单位阶跃函数的LT 0,te) 6(t)= 1 画20<1<) L=) School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 4

4 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 单位阶跃函数的LT 0, 0 ( ) , 0 t u t E t       0 ( ) d ( ) e st U s t u t     0 0 e d e st st E t E s E s          1 L t {1[ ]} s  1 1 0, 0 [ ] 1, 0 t L s t        E=1 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 单位脉冲函数的LT 0 0, ( ) ( ) 1 lim , (0< ) t t t               0 0 1 [ ( )] lim st L t e dt         0 1 lim (1 )s e s        (洛必达法则) 0 0 (1 ) / lim ( ) / lim 1 s s d e d d s d e                  1 L t [1] ( )    Pluse Impluse

幂函数的LT Lt"]=t".e"dt udv+vdu=vu u=1" 1 v=∫e"d=--e" 0- du nt"-dt du du=e-"dt ∫red=”] 用= 1=”.-2.1.1= n School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fa12015 LT性质 一线性定理 (Linearity theorem) L[a时(t)+bf,(】=aF(s)+bF,(s) 徽分定理 (Differentiation theorem) =sF(s)-f0) 积分定理 (Integration theorem) froj-o -一位移定理 (LT of a function multiplied L[e-f(t)]=F(s+a) by a exponential in time) 一延时定理 (LT of a time-shifted function) LLf(t-t】=e-"F(s) 初值定理 f(0)=lim f(t)=lim sF(s) (Initial value theorem,IVT) 终值定理 (Final value theorem,FVT) lim f(t)=lim sF(s) → 3→0 School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 5

5 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 幂函数的LT 0 [ ] e d n st n L t t t     1 0 1 1 e e d 0 st n st n t nt t s s             1 1 e d [ ] n n n st n t t L t s s       0 1 1 2 1 ! [ ] [ ] n n n n n L t L t s s s s s      u u u d d        n u t  d e dst  t   1 d d n u nt t   1 e d e st st t s        2 1 L t[ ] s  2 3 1 1 [ ] 2 L t s  v u v du BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University LT性质 ---微分定理 （Differentiation theorem） ---积分定理 （Integration theorem） ---位移定理 （LT of a function multiplied by a exponential in time） ---延时定理 （LT of a time-shifted function） ---终值定理 (Final value theorem，FVT) ---初值定理 （Initial value theorem, IVT) ---线性定理 （Linearity theorem） d ( ) ( ) (0 ) d f t L sF s f t          1 ( ) (0) ( )d F s f L f t t s s         [ ( )] e ( ) s L f t F s      [e ( )] ( ) at L f t F s a    0 lim ( ) lim ( ) t s f t sF s    0 (0 ) lim ( ) lim ( ) t s f f t sF s       1 2 1 2 L af t bf t aF s bF s [ ( ) ( )] ( ) ( )   

微分定理 9-[9ed=ro-o) df0]=sFs-sf0)-s2f0)--6-f di" 零初始条件(Zero initial condition,ZIC) f0)=f0)=…=0 School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 积分定理 ∫fa)dlo 0]-,0 F+'0+0)++0 零初始条件(Zero initial condition,,ZIC) -(0)=f-2(0)=…=0 ou小-9 School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 6

6 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 微分定理 0 d ( ) d ( ) e d ( ) (0 ) d d st f t f t L t sF s f t t                    ( ) 1 2 ( 2) ( 1) (0 ) (0 ) d ( ) ( ) (0 ) (0 ) d n n n n n n n f t L s F s s f s f sf f t                       ( ) d ( ) ( ) d n n n f t L F s t s        f f (0 ) (0 ) 0        零初始条件（Zero initial condition, ZIC) BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 积分定理 1 ( ) ( )d F s (0) L f t f t s s         1 2 1 ( ) (0 ) (0 ) (0 ) ( )( ) n n n n n n F s f f f L f t dt s s s s                       0 ( )d t f t t   1 2 f f (0) (0) 0      ( ) ( )(d ) n n n F s s L f t t            零初始条件（Zero initial condition, ZIC)

位移定理 Le-"f(=ef()e-"f(t)dt f(e-dt =F(s+) L[sinot]=g子+ 0 L[e“sinot]= School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 延时定理 LLf(t-t)】=erF(s) 1(t) 1.t 0=0 sin(ot+p) 解 解 解1 School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 7

7 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 位移定理 0 [ ] e ( )e ( ) e ) ( d at at st L f t t t f t f       ( ) 0 ( )e d ( ) s t f s t t F          e sin at L t          2 2 L t sin s      BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 延时定理 [ ( )] e ( ) s L f F s t      [解] [解] [解] sin( ) m      t

例1-1) 0◆ 2+0 sin@t L[f(t-t)]=e-"F(s) θ(t)=0nsin(ot+p) School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fa2015 例1-2] ↑ L[f(t-)]=e "F(s) 0,t<0 A f)= A,0≤t<T 0,1≥x 入 School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 8

8 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1-1] ( ) sin( ) m     t t   1 2 2 sin             L t s [ ( )] e ( ) s L f F s t      BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1-2] 0, 0 ( ) , 0 0, t f t A t t             [ ( )] e ( ) s L f F s t     

[例1-3] 1)◆ (t) ) ,t) ous=(1) 1t) School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fa2015 初值定理和终值定理 lim f(t)=limsF(s) 1-0t S→00 lim f(t)=lim sF(s) s→0 School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 9

9 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1-3] BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 初值定理和终值定理 0 lim ( ) lim ( ) t s f t sF s    0 lim ( ) lim ( ) t s f t sF s    

[例2] x(0)=0 1st order ODE 4x+y=10 Zero initial conditon -x+3少+2y=0 U0)=5 Find x(oo)y(oo) u dr sF(s)-f(0) lim f(t)=limsF(s) x(co)=limsX(s)= 0 y(co)=limsY(s)= 50 School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fa12015 部分分式法(Partial-.fraction expansion method) 分子多项式(merator polynomial) F6=B-s产+As叫++b-5+b。 A(s) dos"+as"+....+ais+an msn 分母多项式(denominator polynomial) 根(roots) F(s)= B9-K(s+s+2)(s+m -31,-22,-2m暑点（亿er03） AS)(+Ps+P2).(S+P.）-n,-p2,-P,极点(Po1e8） L[F(s)+F(s)+…+F(s】=f)+f5t)+…+fn) School of Mechanical Engineering ME369-Lecture 3.1 Shanghai Jiao Tong University Fall 2015 10

10 BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例2] 4 10 3 2 0 x y x y y         (0) 0 (0) 5 x y      x( )  y( )  0 0 ( ) lim ( ) ( ) lim ( ) s s x sX s y sY s             d ( ) ( ) (0 ) d f t L sF s f t          0 lim ( ) lim ( ) t s f t sF s    1 st order ODE Zero initial conditon Find BE315-Lecture 3.2 Fall 2011 ME369 Lecture 3.1 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 0 1 1 1 0 1 1 ( ) .... ( ) ( ) .... m m m m n n n n B s b s b s b s b F s A s a s a s a s a               ( )( )...( ) ( )( )...( ) ( ) ( ) ( ) 1 2 1 2 n m s p s p s p K s z s z s z A s B s F s         1 2 , ,..., n    p p p 1 2 , ,..., m    z z z 极点（Poles） 零点 (Zeros） 1 1 2 1 2 [ ( ) ( ) ( )] ( ) ( ) ( ) L F s F s F s f t f t f t n n         部分分式法(Partial-fraction expansion method) 分母多项式（denominator polynomial） 分子多项式（numerator polynomial） m<n 根（roots）