
ME369-系统模型、分折与控制 4.3信号流图 School of Mechanical Engineering ME369-Lecture 4.3 Shanghai Jiao Tong University Fall 2015 信号流图(signal-flow graph)的定义 图示法来描述线性代数方程 x2=x+ex; x3=2+4 X4=bx3 xs=dx,+cxa+gxs d g X3 School of Mechanical Engineering ME369-Lecture 4.3 Shanghai Jiao Tong University Fall 2015 1
1 ME369-Lecture 4.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 4.3 信号流图 ME 369– 系统模型、分析与控制 ME369-Lecture 4.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 信号流图(signal-flow graph)的定义 图示法来描述线性代数方程 2 1 3 3 2 4 4 3 5 2 4 5 x x ex x ax fx x bx x dx cx gx
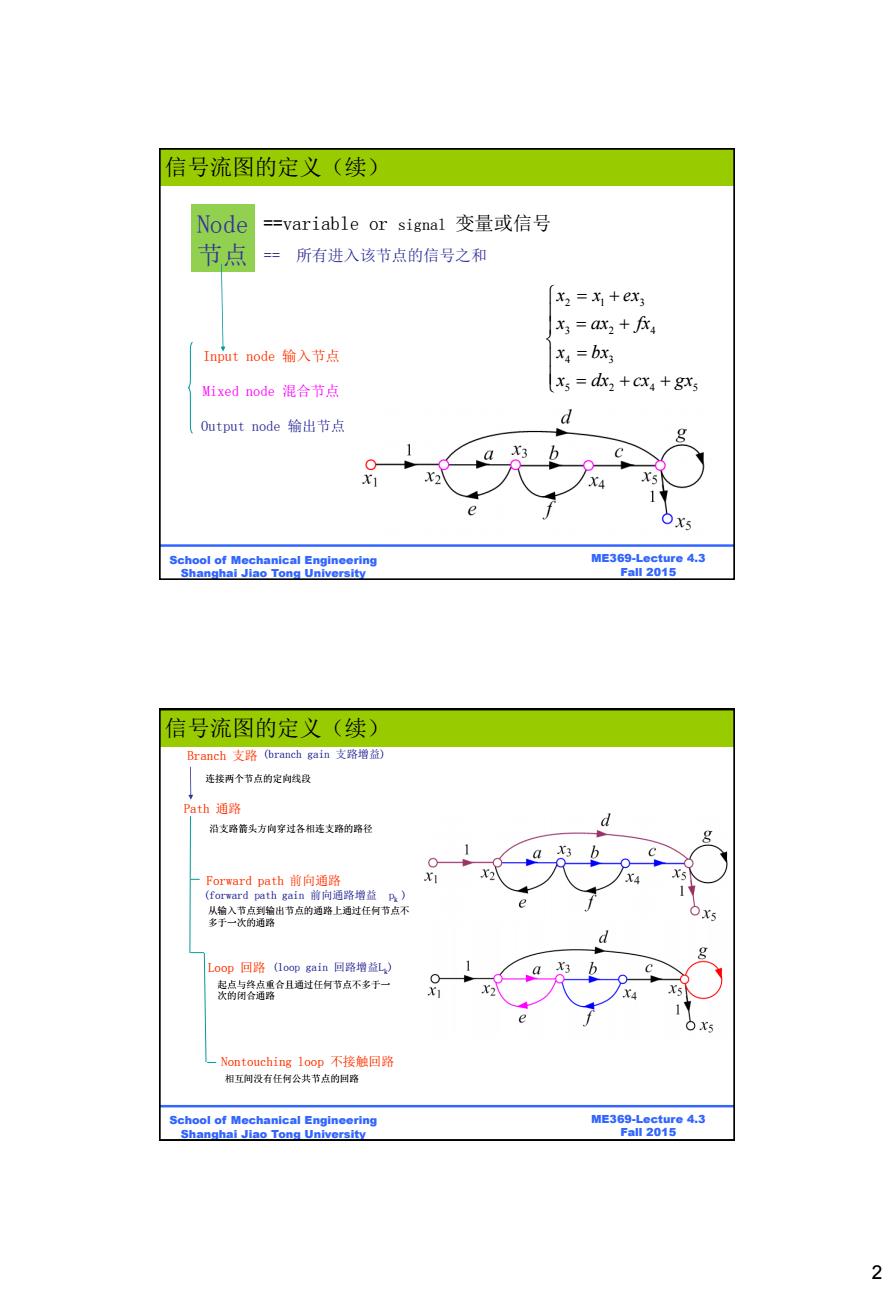
信号流图的定义(续) Node =variable or signal变量或信号 节点 所有进入该节点的信号之和 X2=x+ex; X3 =ax2+fx Input node输入节点 X4 =bxs Mixed node混合节点 x=2+Cx4+g5 Output node输出节点 d X3 X5 School of Mechanical Engineering ME369-Lecture 4.3 Shanghai Jiao Tong University Fall 2015 信号流图的定义(续) Branch支路(branch gain支路增益) 连接两个节点的定向线段 Path通路 沿支路箭头方向穿过各相连支路的路径 Forward path前向通路 (forward path gain前向通路增益B) 从输入节点到输出节点的通路上通过任月节点不 多于一次的通路 Loop回路(1 oop gain回路增益L,) 起点与终点重合且通过任月节点不多于一 次的闭合通路 -Nontouching loop不接触回路 相互间没有任何公共节点的回路 School of Mechanical Engineering ME369-Lecture 4.3 Shanghai Jiao Tong University Fall 2015 2
2 ME369-Lecture 4.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Node ==variable or signal 变量或信号 节点 2 1 3 3 2 4 4 3 5 2 4 5 x x ex x ax fx x bx x dx cx gx == 所有进入该节点的信号之和 Input node 输入节点 Output node 输出节点 Mixed node 混合节点 信号流图的定义(续) ME369-Lecture 4.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Branch 支路 (branch gain 支路增益) 连接两个节点的定向线段 Forward path 前向通路 (forward path gain 前向通路增益 pk ) Loop 回路 起点与终点重合且通过任何节点不多于一 次的闭合通路 (loop gain 回路增益Lk) 从输入节点到输出节点的通路上通过任何节点不 多于一次的通路 Nontouching loop 不接触回路 相互间没有任何公共节点的回路 Path 通路 沿支路箭头方向穿过各相连支路的路径 信号流图的定义(续)

[例1]由微分方程组绘制信号流图 u,(t)-4(t) =i,(t) U,s)-U=1,s) R R 40=2e0-60咖 LT U=4)-46 Cs 4,0-.@=i,0 Us)-U@=1,s) R R U)= 2(s) C2s School of Mechanical Engineering ME369-Lecture 4.3 Shanghai Jiao Tong University Fall 2015 [例1]绘制信号流图(续) U.(6)-U,()-1(6s) R Us-U@=1,) R -1 1/R U.(s) 1(s) U,(s) I(8) U.() -1 1 U,)=49-s U.=1,o Cs C.s School of Mechanical Engineering ME369-Lecture 4.3 Shanghai Jiao Tong University Fall 2015 3
3 ME369-Lecture 4.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 1 1 ( ) ( ) ( ) r u t u t i t R 1 1 2 1 1 u t i t i t t ( ) [ ( ) ( )]d C 1 2 2 ( ) ( ) ( ) c u t u t i t R 2 2 1 ( ) ( )d c u t i t t C 1 1 1 ( ) ( ) ( ) U s U s r I s R 1 2 1 1 ( ) ( ) ( ) I s I s U s C s 1 2 2 ( ) ( ) ( ) U s U s c I s R 2 2 1 ( ) ( ) U s I s c C s LT [例1]由微分方程组绘制信号流图 ME369-Lecture 4.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 1 1 ( ) ( ) ( ) U s U s r I s R 1 2 2 ( ) ( ) ( ) U s U s c I s R 2 2 1 ( ) ( ) U s I s c C s 1 2 1 1 ( ) ( ) ( ) I s I s U s C s [例1]绘制信号流图(续)
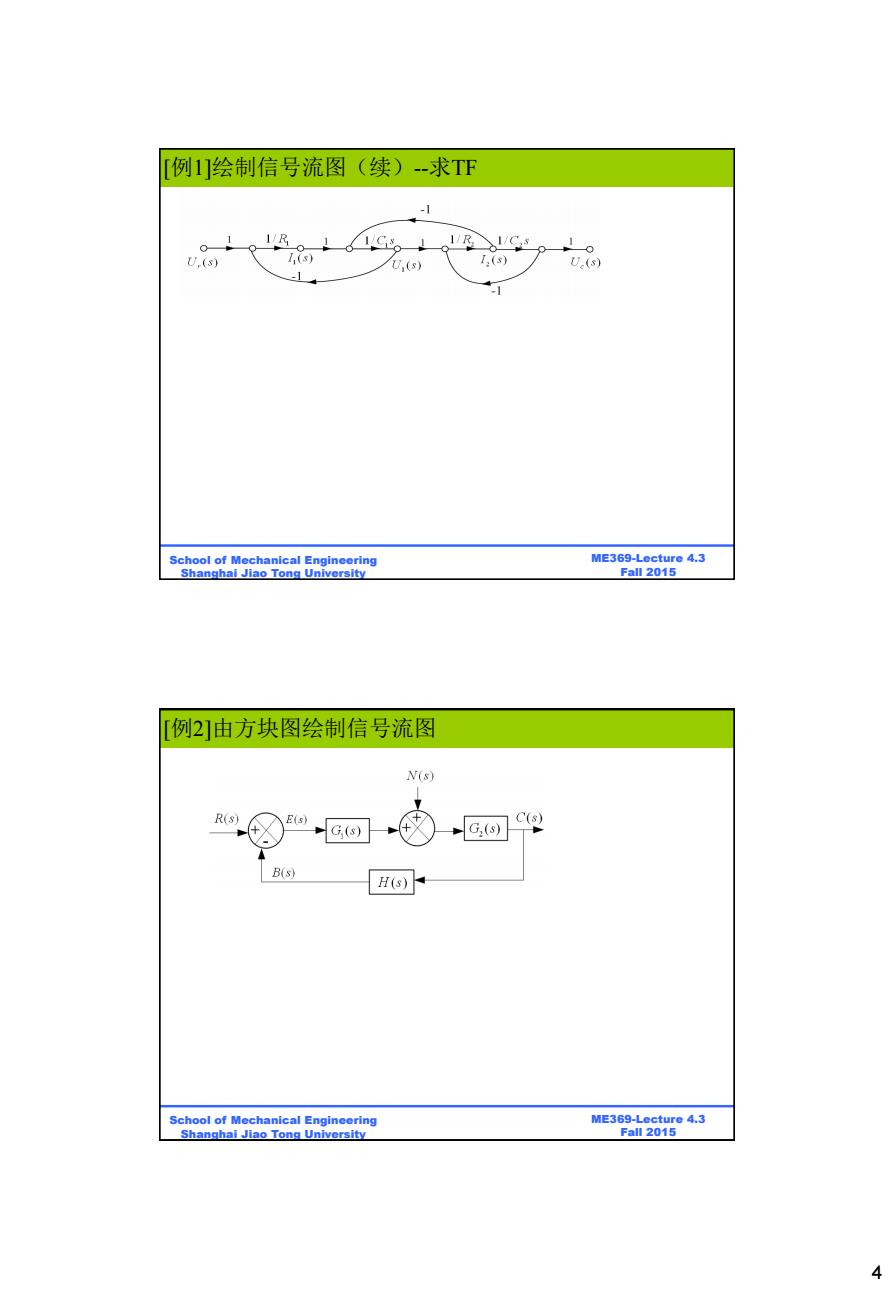
[例1]绘制信号流图(续)-求T℉ 1 1/R I/R I/C.s U,(s) I,(s) U,(8) I2(s) U(s) -1 School of Mechanical Engineering ME369-Lecture 4.3 Shanghai Jiao Tong University Fall 2015 例2]由方块图绘制信号流图 N(s) R(s) E(s) G() B(s) H(s) School of Mechanical Engineering ME369-Lecture 4.3 Shanghai Jiao Tong University Fall 2015 4
4 ME369-Lecture 4.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1]绘制信号流图(续)--求TF ME369-Lecture 4.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [Drawing a signal 例2]由方块图绘制信号流图 -flow graph : from a block diagram

信号流图的梅逊公式 一第k条前向通路的传递函数(通路增益 Gs)=∑PA 第k条前向通路特征式的余因子 △k= △中,将与第k条前向通路相接触的回路增益代以零值 流图特征式 A=1-∑L。+∑L2,-∑L++(-l)∑Lm ∑4w 一所有不同回路的增益和: ∑4a 一每两个互不接触回路增益乘积之和 ∑l, 一每三个互不接触回路增益乘积之和 ∑4 一任何m个互不接触回路增益乘积之和 School of Mechanical Engineering ME369-Lecture 4.3 Shanghai Jiao Tong University Fall 2015 例3]梅逊公式求取T℉ School of Mechanical Engineering ME369-Lecture 4.3 Shanghai Jiao Tong University Fall 2015 5
5 ME369-Lecture 4.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University —第k条前向通路的传递函数(通路增益) 流图特征式 —第k条前向通路特征式的余因子 1 ∆中,将与第k 条前向通路相接触的回路增益代以零值 1 ( ) k k n k G s P (2) (3) ( ) (1) 1 ... ( 1)m L L L L m —所有不同回路的增益和; —每两个互不接触回路增益乘积之和 —每三个互不接触回路增益乘积之和 —任何m个互不接触回路增益乘积之和 L(1) L(2) L(3) L(m) 信号流图的梅逊公式 ME369-Lecture 4.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例3]梅逊公式求取TF
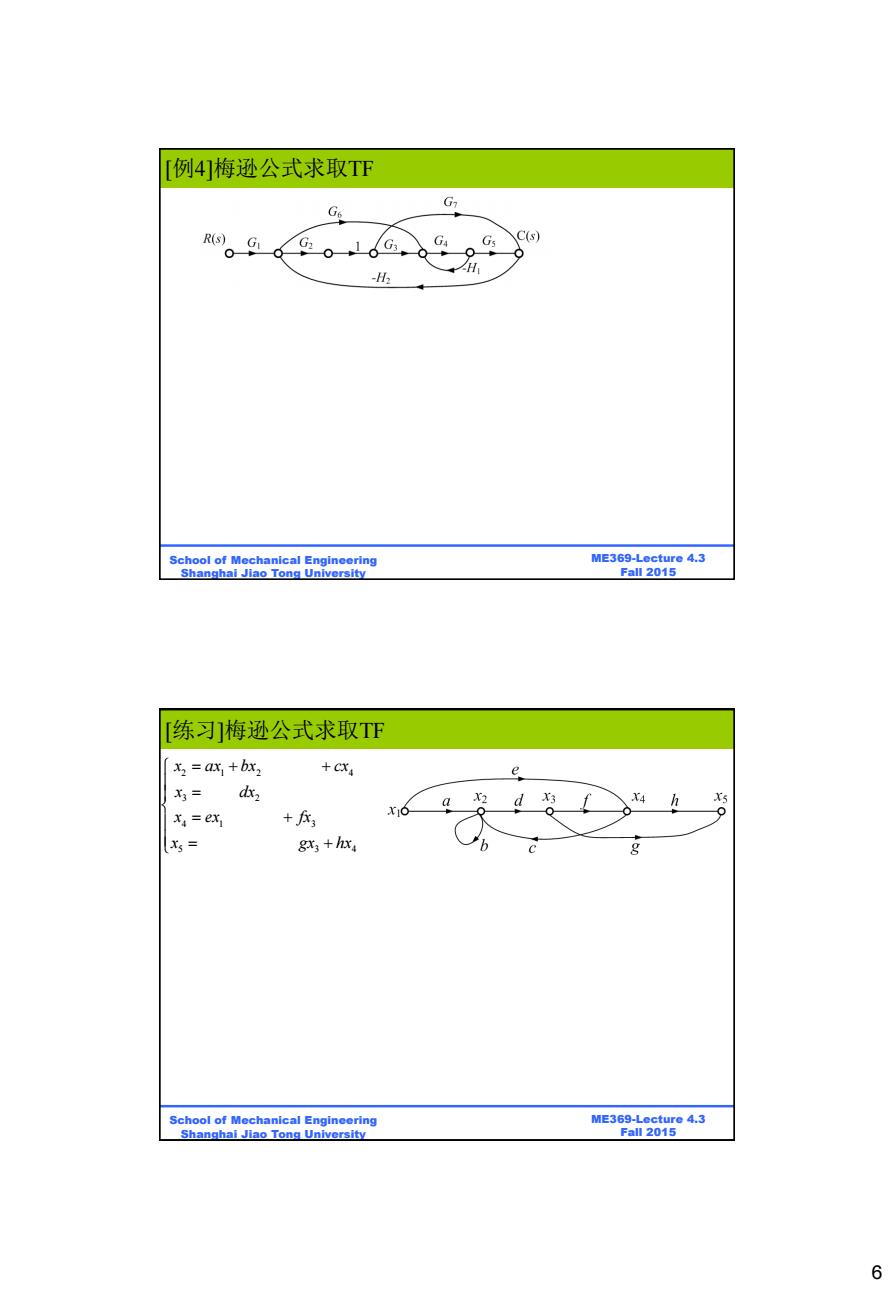
T例4]梅逊公式求取TF R(s) GA Gs C(s) ●) -2 H School of Mechanical Engineering ME369-Lecture 4.3 Shanghai Jiao Tong University Fall 2015 练习]梅逊公式求取T℉ x2=ax +bx2 +C4 X3= dx, X5 x=ex +瓜3 x16 d X4 ● Xs= gx;+hxs School of Mechanical Engineering ME369-Lecture 4.3 Shanghai Jiao Tong University Fall 2015 6
6 ME369-Lecture 4.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例4]梅逊公式求取TF ME369-Lecture 4.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 2 1 2 4 3 2 4 1 3 5 3 4 x ax bx cx x dx x ex fx x gx hx [练习]梅逊公式求取TF