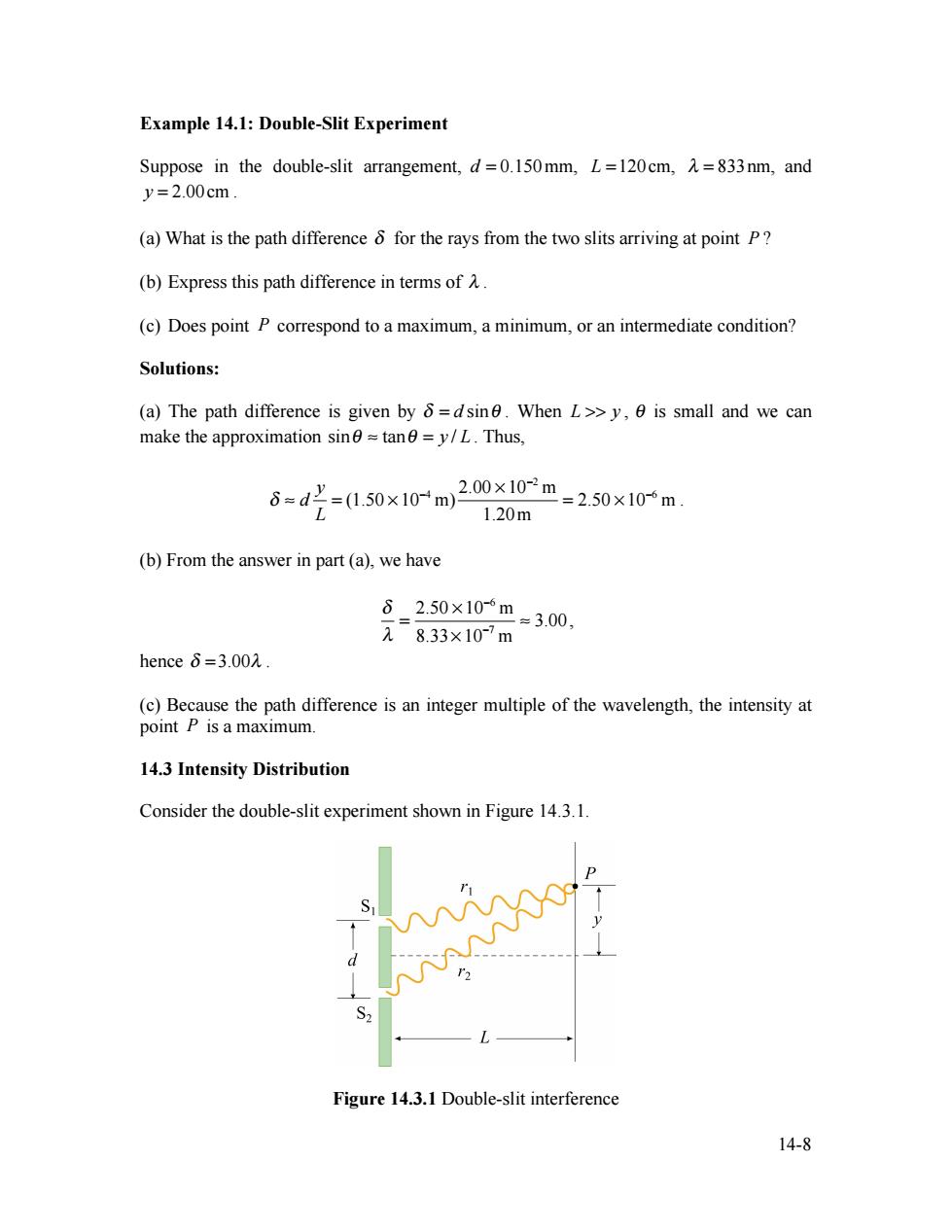
Example 14.1:Double-Slit Experiment Suppose in the double-slit arrangement,d=0.150mm,L=120cm,=833nm,and y=2.00cm. (a)What is the path difference 8 for the rays from the two slits arriving at point P? (b)Express this path difference in terms ofA. (c)Does point P correspond to a maximum,a minimum,or an intermediate condition? Solutions: (a)The path difference is given by 8=dsin.When L>>y,0 is small and we can make the approximation sin≈tanθ=y/L.Thus, 6=d'=(0.50×10-m 2.00×10-m=2.50×10m. 1.20m (b)From the answer in part(a),we have 62.50×10-6m 元8.33×10-7m =3.00, henceδ=3.002. (c)Because the path difference is an integer multiple of the wavelength,the intensity at point P is a maximum. 14.3 Intensity Distribution Consider the double-slit experiment shown in Figure 14.3.1. Figure 14.3.1 Double-slit interference 14-814-8 Example 14.1: Double-Slit Experiment Suppose in the double-slit arrangement, d = 0.150mm, L =120cm, λ = 833nm, and y = 2.00cm . (a) What is the path difference δ for the rays from the two slits arriving at point P ? (b) Express this path difference in terms of λ . (c) Does point P correspond to a maximum, a minimum, or an intermediate condition? Solutions: (a) The path difference is given by δ = d sinθ . When L >> y , θ is small and we can make the approximation sinθ ≈ tanθ = y / L . Thus, δ ≈ d y L = (1.50 × 10−4 m) 2.00 × 10−2 m 1.20m = 2.50 × 10−6 m . (b) From the answer in part (a), we have δ λ = 2.50 × 10−6 m 8.33× 10−7 m ≈ 3.00, hence δ = 3.00λ . (c) Because the path difference is an integer multiple of the wavelength, the intensity at point P is a maximum. 14.3 Intensity Distribution Consider the double-slit experiment shown in Figure 14.3.1. Figure 14.3.1 Double-slit interference