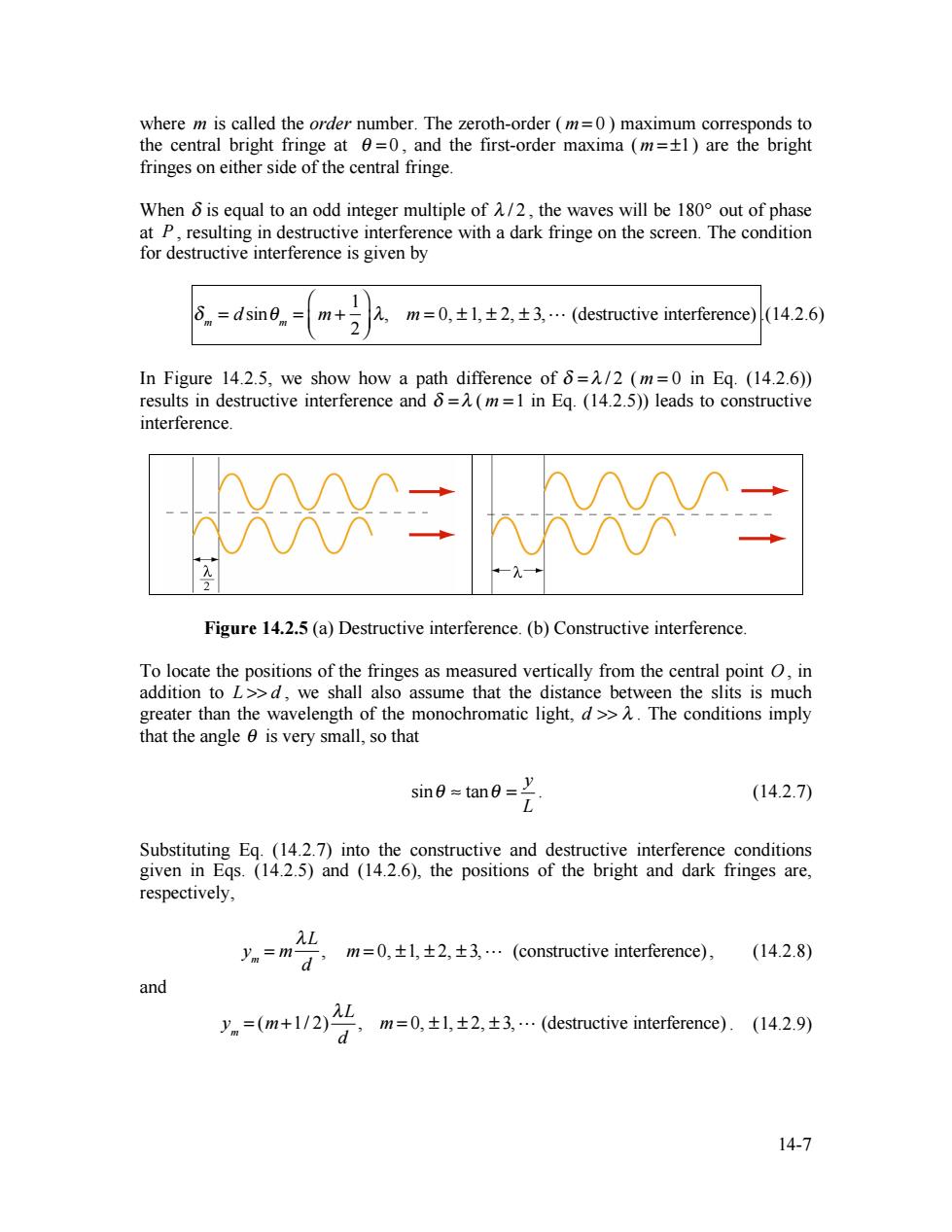
where m is called the order number.The zeroth-order (m=0)maximum corresponds to the central bright fringe at 0=0,and the first-order maxima (m=+1)are the bright fringes on either side of the central fringe. When 6 is equal to an odd integer multiple of A/2,the waves will be 180 out of phase at P,resulting in destructive interference with a dark fringe on the screen.The condition for destructive interference is given by δnm=dsin6n= m+2 2,m=0,±l,±2，±3，…(destructive interference) (14.2.6) In Figure 14.2.5,we show how a path difference of =/2 (m=0 in Eq.(14.2.6)) results in destructive interference and 6=(m=1 in Eq.(14.2.5))leads to constructive interference. XX二 Figure 14.2.5(a)Destructive interference.(b)Constructive interference To locate the positions of the fringes as measured vertically from the central point O,in addition to L>>d,we shall also assume that the distance between the slits is much greater than the wavelength of the monochromatic light,d>>.The conditions imply that the angle 0 is very small,so that sin=tan= (14.2.7) Substituting Eq.(14.2.7)into the constructive and destructive interference conditions given in Eqs.(14.2.5)and (14.2.6),the positions of the bright and dark fringes are, respectively, L y =m- a,m=0,±l,±2，±3…(oructiveinrrence)), (14.2.8) and =(m+1/2)2 ,m=0,±l,±2，±3，(destructiveintre).(l429y 14-714-7 where m is called the order number. The zeroth-order ( m = 0 ) maximum corresponds to the central bright fringe at θ = 0 , and the first-order maxima ( m = ±1) are the bright fringes on either side of the central fringe. When δ is equal to an odd integer multiple of λ / 2 , the waves will be 180° out of phase at P , resulting in destructive interference with a dark fringe on the screen. The condition for destructive interference is given by δ m = d sinθ m = m + 1 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ λ, m = 0, ± 1, ± 2, ± 3, (destructive interference) .(14.2.6) In Figure 14.2.5, we show how a path difference of δ = λ / 2 ( m = 0 in Eq. (14.2.6)) results in destructive interference and δ = λ ( m =1 in Eq. (14.2.5)) leads to constructive interference. Figure 14.2.5 (a) Destructive interference. (b) Constructive interference. To locate the positions of the fringes as measured vertically from the central point O , in addition to L >> d , we shall also assume that the distance between the slits is much greater than the wavelength of the monochromatic light, d >> λ . The conditions imply that the angle θ is very small, so that sin tan y L θ ≈ θ = . (14.2.7) Substituting Eq. (14.2.7) into the constructive and destructive interference conditions given in Eqs. (14.2.5) and (14.2.6), the positions of the bright and dark fringes are, respectively, ym = m λL d , m = 0, ±1, ± 2, ± 3, (constructive interference), (14.2.8) and ym = (m+1/ 2) λL d , m = 0, ±1, ± 2, ± 3, (destructive interference) . (14.2.9)