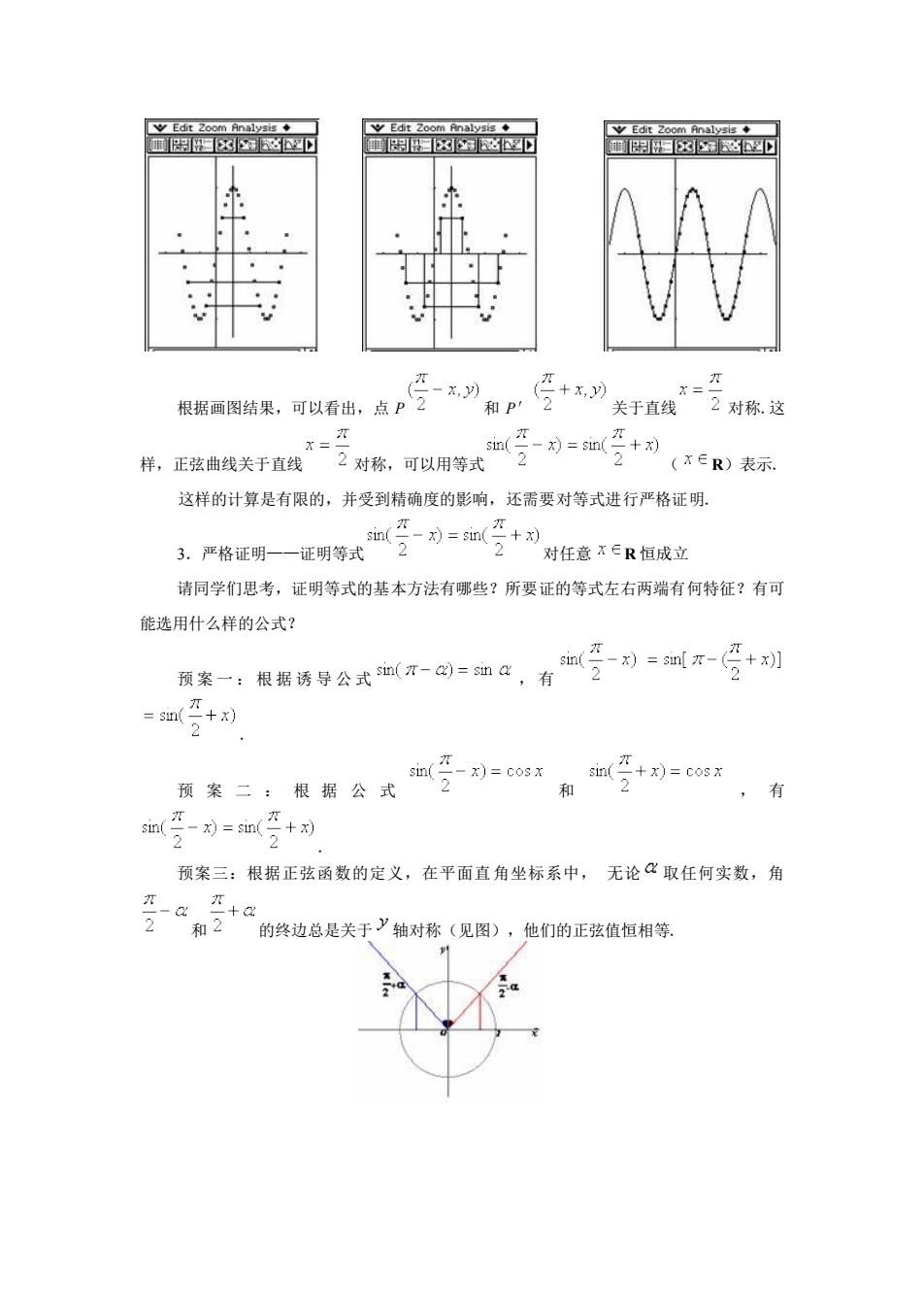
yEt2oAn◆ wEdt2 oom Bnalysis◆ 图x6多Y 图☒离D 关于直艺对称这 这样的计算是有限的，并受到精确度的影响，还需要对等式进行严格证明。 对任意x∈R恒成立 请同学们思考，证明等式的基本方法有哪些？所要证的等式左右两端有何特征？有可 能选用什么样的公式？ 要：限帮涛学公式-回如6，有如空司到-召别 双案二，根聚会式如（写列=cx m(+)=co8x 和 ，有 预案三：根据正弦函数的定义，在平面直角坐标系中，无论取任何实数，角 的终边总是关于》轴对称（见图），他们的正弦值恒相等。 根据画图结果，可以看出，点 P 和 P′ 关于直线 对称.这 样，正弦曲线关于直线 对称，可以用等式 （ R）表示. 这样的计算是有限的，并受到精确度的影响，还需要对等式进行严格证明. 3．严格证明——证明等式 对任意 R 恒成立 请同学们思考，证明等式的基本方法有哪些？所要证的等式左右两端有何特征？有可 能选用什么样的公式？ 预案一：根据诱导公式 ， 有 . 预 案 二 ： 根 据 公 式 和 ， 有 . 预案三：根据正弦函数的定义，在平面直角坐标系中， 无论 取任何实数，角 和 的终边总是关于 轴对称（见图），他们的正弦值恒相等