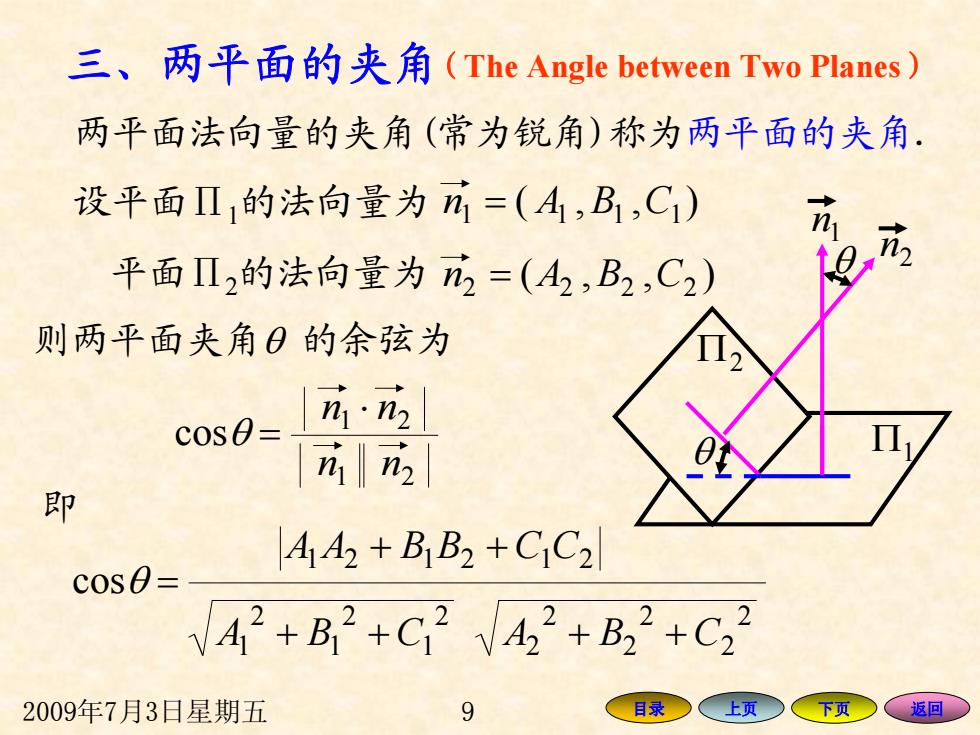
三、两平面的夹角(The Angle between Two Planes) 两平面法向量的夹角（常为锐角）称为两平面的夹角. 设平面Π1的法向量为n1=（A1,B1,C1) 平面Ⅱ2的法向量为2=(A2,B2,C2) 则两平面夹角0的余弦为 cos0= n应 in2 即 A42+B B2+C C2 c0S0= V42+B2+C7V42+B22+C22 2009年7月3日星期五 9 目录 上页 下页 返回 2009年7月3日星期五 9 目录 上页 下页 返回 三、两平面的夹角 设平面 ∏ 1的法向量为 平面 ∏ 2的法向量为 则两平面夹角 θ 的余弦为 cos θ = 即 + + CCBBAA 212121 2 2 2 2 2 2 ++ CBA 2 1 2 1 2 1 ++ CBA 两平面法向量的夹角(常为锐角)称为两平面的夹角. Π 1 Π 2 θ 2 n 1 n θ ),( = An B C1111 ),( = An B C2222 21 21 cos nn ⋅ nn θ = （The Angle between Two Planes ）