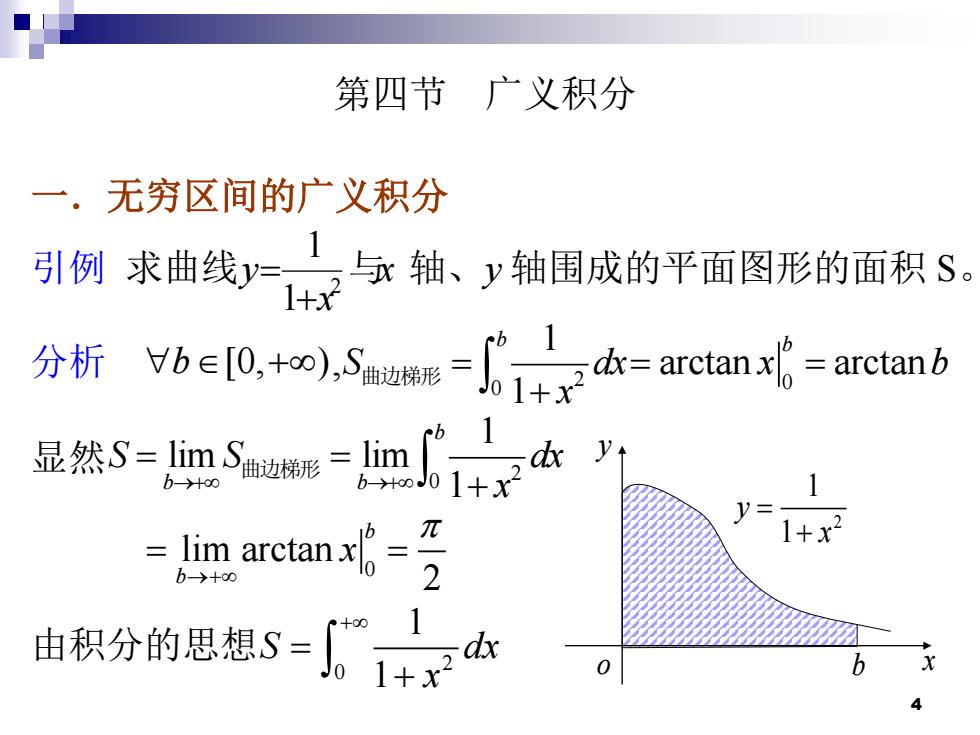
第四节广义积分 一.无穷区间的广义积分 引例求面线中轴、：箱围成的半面图形的面积S, 分析he0,+ess-1十子-c或-arean 显然s=mSe=m 6+oJ01+x V= =lim arctan x 1+x2 b→+00 由积分的思想S=1+ r+o01 。dx4 第四节 广义积分 一．无穷区间的广义积分 引例 求曲线 2 1 1 y x = + 与x 轴、y 轴围成的平面图形的面积 S。 分析   + b [0, ), 2 0 1 1 b S dx x = + 曲边梯形  0 arctan arctan b = = x b 显然 2 0 1 lim lim 1 b b b S S dx →+ →+ x = = + 曲边梯形  0 lim arctan 2 b b x  →+ = = 由积分的思想 2 0 1 1 S dx x + = +  y o b x 2 1 1 y x = +