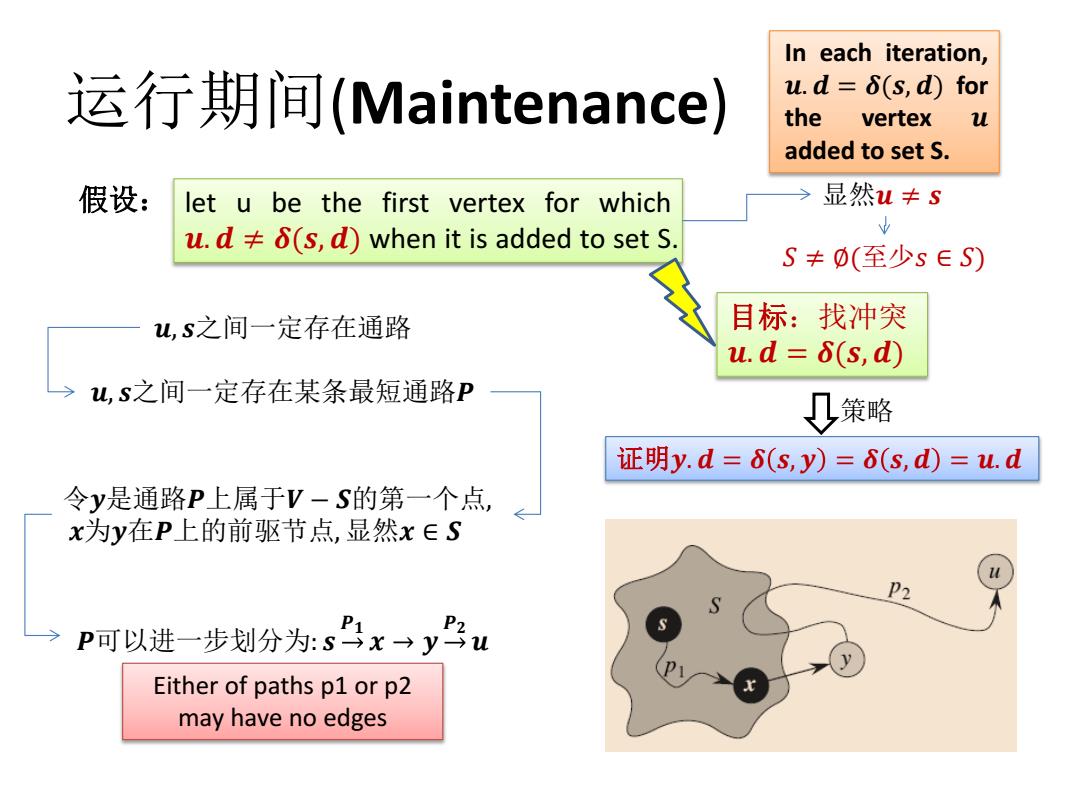
In each iteration, 运行期间(Maintenance) u.d =6(s,d)for the vertex u added to set S. 假设： let u be the first vertex for which 显然u≠s u.d≠δ(s,d)when it is added to set S. 出 S≠0（至少s∈S) u,s之间一定存在通路 目标：找冲突 u.d= 6(s,d) u,S之间一定存在某条最短通路P 策略 证明y.d=6(s,y)=6(s,d)=u.d 令y是通路P上属于V-S的第一个点， x为y在P上的前驱节点，显然x∈S P2 P可以进一步划分为：sx→yu P1 Either of paths p1 or p2 may have no edges运行期间(Maintenance) In each iteration, 𝒖. 𝒅 = 𝜹(𝒔, 𝒅) for the vertex 𝒖 added to set S. 显然𝒖 ≠ 𝒔 let u be the first vertex for which 𝒖. 𝒅 ≠ 𝜹(𝒔, 𝒅) when it is added to set S. 假设： 𝑆 ≠ ∅(至少𝑠 ∈ 𝑆) 𝒖, 𝒔之间一定存在通路 𝒖, 𝒔之间一定存在某条最短通路𝑷 令𝒚是通路𝑷上属于𝑽 − 𝑺的第一个点, 𝒙为𝒚在𝑷上的前驱节点, 显然𝒙 ∈ 𝑺 𝑷可以进一步划分为: 𝒔 𝑷𝟏 𝒙 → 𝒚 𝑷𝟐 𝒖 Either of paths p1 or p2 may have no edges 目标：找冲突 𝒖. 𝒅 = 𝜹(𝒔, 𝒅) 证明𝒚. 𝒅 = 𝜹 𝒔, 𝒚 = 𝜹 𝒔, 𝒅 = 𝒖. 𝒅 策略