
Dijkstra算法正确性
Dijkstra算法 正确性
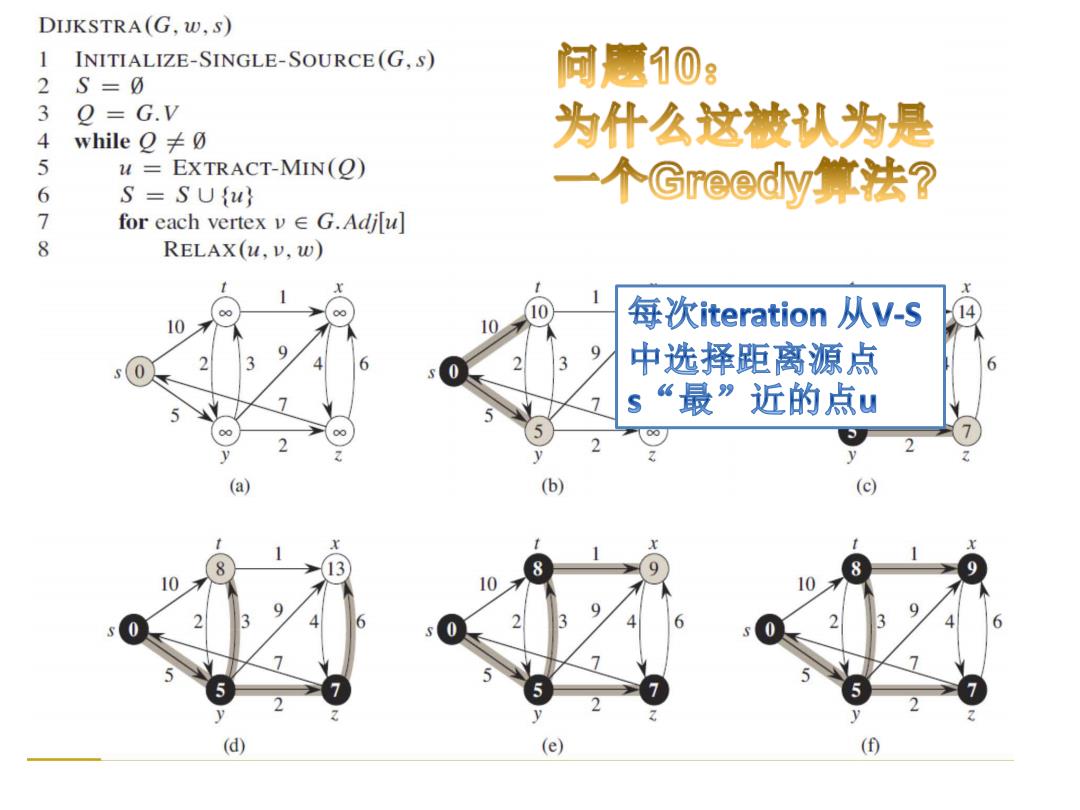
DIJKSTRA(G,w,s) 1 INITIALIZE-SINGLE-SOURCE(G,S) 2 问题1@8 S=0 3 O=G.V 4 while O≠0 为什么这被认为是 5 24= EXTRACT-MIN(O) 6 S=SUfu 一个Greedy.算法? 7 for each vertex v G.Adjlu] 8 RELAX(u,v,w) 10 14 10 10 每次iteration从V-S 9 9 3 3 中选择距离源点 6 “最”近的点u 00 (a) (b) (c) r 8 13 8 9 8 9 10 10 10 9 2 3 6 3 6 5 (d) (e) (f)

DIJKSTRA(G.w.s) 1 INITIALIZE-SINGLE-SOURCE(G.S) 2S=0 3 0=G.V Dijkstra算法正确性 4 while O≠0 5 EXTRACT-MIN(O) 6 S=SUfu 7 for each vertex vE G.Adjlu] 8 RELAX(u.V.w) Corollary 24.7 If we run Dijkstra's algorithm on a weighted,directed graph G =(V,E)with nonnegative weight function w and source s,then at termination,the predecessor subgraph G is a shortest-paths tree rooted at s. predecessor-subgraph property Theorem 24.6 (Correctness of Dijkstra's algorithm) Dijkstra's algorithm,run on a weighted,directed graph G =(V,E)with non- negative weight function w and source s,terminates with u.d =8(s,u)for all vertices u e V
Dijkstra算法 正确性 predecessor-subgraph property

DIJKSTRA(G.w.s) 1 INITIALIZE-SINGLE-SOURCE(G.S) 2 S=0 3 O=G.V Dijkstra算法正确性 4 while O≠g 5 EXTRACT-MIN(O) 6 S=SUfu 7 for each vertex vE G.Adjlu] 8 RELAX(u.V.w) Theorem 24.6(Correctness of Dijkstra's algorithm) Dijkstra's algorithm,run on a weighted,directed graph G=(V,E)with non- negative weight function w and source s,terminates with u.d =8(s,u)for all vertices u e V. Proof We use the following loop invariant: At the start of each iteration of the while loop of lines 4-8,v.d 8(s,v) for each vertex v∈S. It suffices to show for each vertex u E V,we have u.d =8(s.u)at the time when u is added to set S.Once we show that u.d =8(s.u),we rely on the upper-bound property to show that the equality holds at all times thereafter
Dijkstra算法 正确性

DIJKSTRA(G.w.s) 1 INITIALIZE-SINGLE-SOURCE(G.S) 2S=0 3 0=G.V Dijkstra算法正确性 4 while O≠0 5 EXTRACT-MIN(O) 6 S=SUu 7 for each vertex v G.Adjlu] 8 RELAX(.v.w) 初始阶段(Initialization): -S=0,不变式显然成立 0 运行期间(Maintenance): We wish to show that in each iteration,u.d =o(s,d)for the vertex u added to set S. ·终止时刻(Termination) Termination:At termination,=0 which,along with our earlier invariant that O=V-S,implies that S=V.Thus,u.d =8(s,u)for all vertices u V
Dijkstra算法 正确性 • 初始阶段(Initialization): – 𝑆 = ∅, 不变式显然成立 • 运行期间(Maintenance): – We wish to show that in each iteration, 𝒖. 𝒅 = 𝜹(𝒔, 𝒅) for the vertex 𝒖 added to set S. • 终止时刻(Termination)
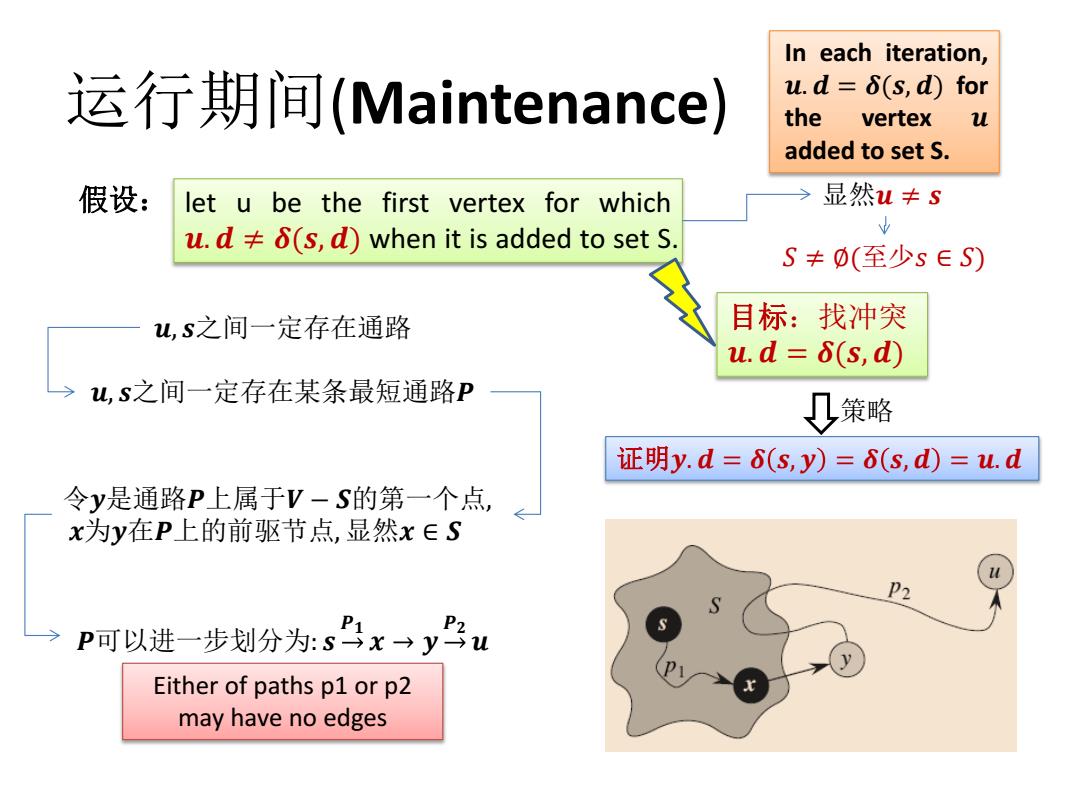
In each iteration, 运行期间(Maintenance) u.d =6(s,d)for the vertex u added to set S. 假设: let u be the first vertex for which 显然u≠s u.d≠δ(s,d)when it is added to set S. 出 S≠0(至少s∈S) u,s之间一定存在通路 目标:找冲突 u.d= 6(s,d) u,S之间一定存在某条最短通路P 策略 证明y.d=6(s,y)=6(s,d)=u.d 令y是通路P上属于V-S的第一个点, x为y在P上的前驱节点,显然x∈S P2 P可以进一步划分为:sx→yu P1 Either of paths p1 or p2 may have no edges
运行期间(Maintenance) In each iteration, 𝒖. 𝒅 = 𝜹(𝒔, 𝒅) for the vertex 𝒖 added to set S. 显然𝒖 ≠ 𝒔 let u be the first vertex for which 𝒖. 𝒅 ≠ 𝜹(𝒔, 𝒅) when it is added to set S. 假设: 𝑆 ≠ ∅(至少𝑠 ∈ 𝑆) 𝒖, 𝒔之间一定存在通路 𝒖, 𝒔之间一定存在某条最短通路𝑷 令𝒚是通路𝑷上属于𝑽 − 𝑺的第一个点, 𝒙为𝒚在𝑷上的前驱节点, 显然𝒙 ∈ 𝑺 𝑷可以进一步划分为: 𝒔 𝑷𝟏 𝒙 → 𝒚 𝑷𝟐 𝒖 Either of paths p1 or p2 may have no edges 目标:找冲突 𝒖. 𝒅 = 𝜹(𝒔, 𝒅) 证明𝒚. 𝒅 = 𝜹 𝒔, 𝒚 = 𝜹 𝒔, 𝒅 = 𝒖. 𝒅 策略

证明y.d=6(s,y)=(s,d)=u.d Convergence property (Lemma 24.14) If suv is a shortest path in G for some u,vV,and if u.d 8(s,u)at any time prior to relaxing edge (u,v),then v.d =8(s,v)at all times afterward. ·y.d=6(s,y) Convergence property x.d=6(s,x) when x is added to S Edge (x,y)was relaxed y.d=6(s,y) P是s→u最短路径 >p1+(x→y)是s→y最短路径 y.d 8(s,y) ≤ 6(s,) y.d=6(s,y) P2 ≤ u.d =6(S,d) u.d u.d≤y.d Dijkstra算法保证
证明𝒚. 𝒅 = 𝜹 𝒔, 𝒚 = 𝜹 𝒔, 𝒅 = 𝒖. 𝒅 • 𝒚. 𝒅 = 𝜹 𝒔, 𝒚 when 𝑥 is added to 𝑺 𝒙. 𝒅 = 𝜹 𝒔, 𝒙 Edge 𝒙, 𝒚 was relaxed P是𝑠 → 𝑢最短路径 𝒚. 𝒅 = 𝜹 𝒔, 𝒚 Convergence property 𝒚. 𝒅 = 𝜹 𝒔, 𝒚 = 𝜹 𝒔, 𝒅 = 𝒖. 𝒅 𝑝1 + (𝑥 → 𝑦)是𝑠 → 𝑦最短路径 Dijkstra算法保证
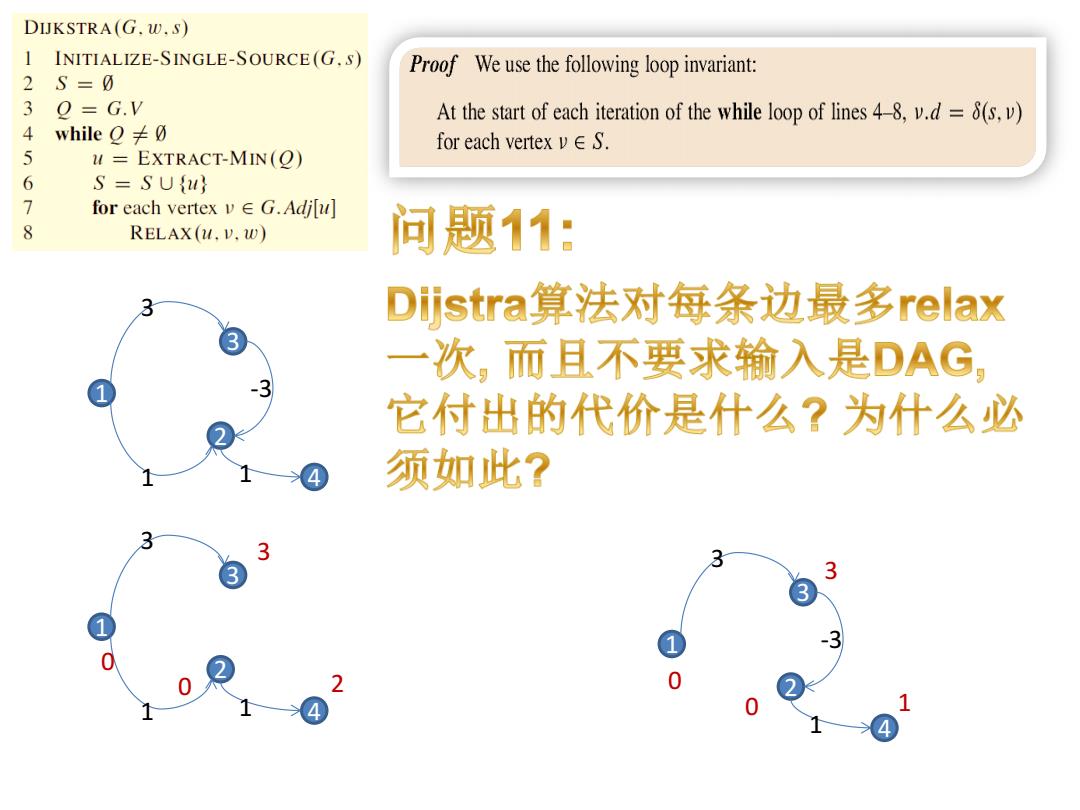
DIJKSTRA(G.w.s) 1 INITIALIZE-SINGLE-SOURCE(G.S) Proof We use the following loop invariant: 2S=0 3 0=G.V At the start of each iteration of the while loop of lines 4-8,v.d=(s,v) 4 while O≠g for each vertex v∈S. 5 EXTRACT-MIN(O) 6 S=SUfu 7 for each vertex v G.Adjlu] 8 RELAX(u.V.w) 问题11: 3 Diistra算法对每条边最多relax 一次,而且不要求输入是DAG 它付出的代价是什么?为什么必 须如此? 3 3 3 3 0 0
2 1 3 13 - 3 1 4 2 1 3 3 - 3 1 4 0 3 0 1 2 1 3 13 1 4 0 3 0 2
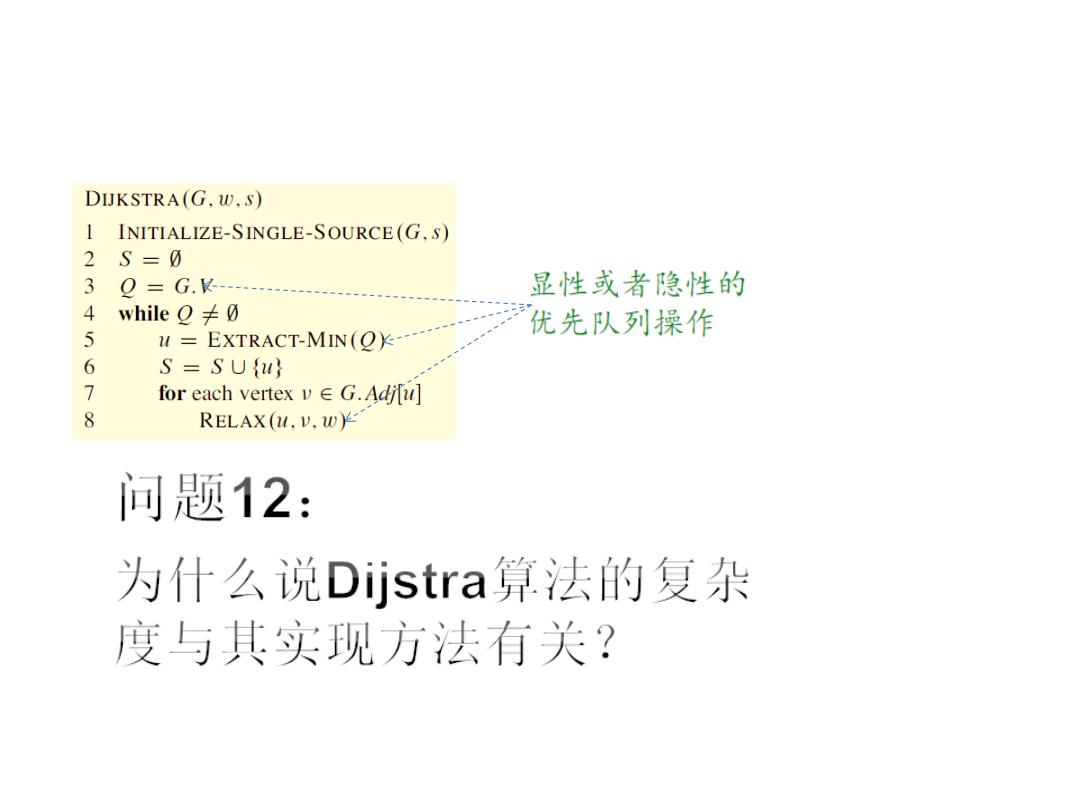
DIJKSTRA(G.w,S) 1 INITIALIZE-SINGLE-SOURCE(G.S) 2S=0 3 O=G.V 显性或者隐性的 4 while O≠g 5 EXTRACT-MIN(O- 优先队列操作 6 S=SUfu 7 for each vertex v G.Adifu] 8 RELAX(u,V.w) 问题12: 为什么说Dijstra算法的复杂 度与其实现方法有关?

问题13: 你能比较一下Dijstra.算法与计 算最小生成树的Prim算法吗? Dijstra算法的结果是否一定是 一个最小生成树?