
计算机问题求解一论题31 。动态规划 2014年09月3日
计算机问题求解 – 论题3-1 - 动态规划 2014 年09 月 3 日

Fibonacci:F=F+F2 间题1: 如果要你计算第n个 Fibonacci数,你用递归还是 用循环,还是随便?为什么?
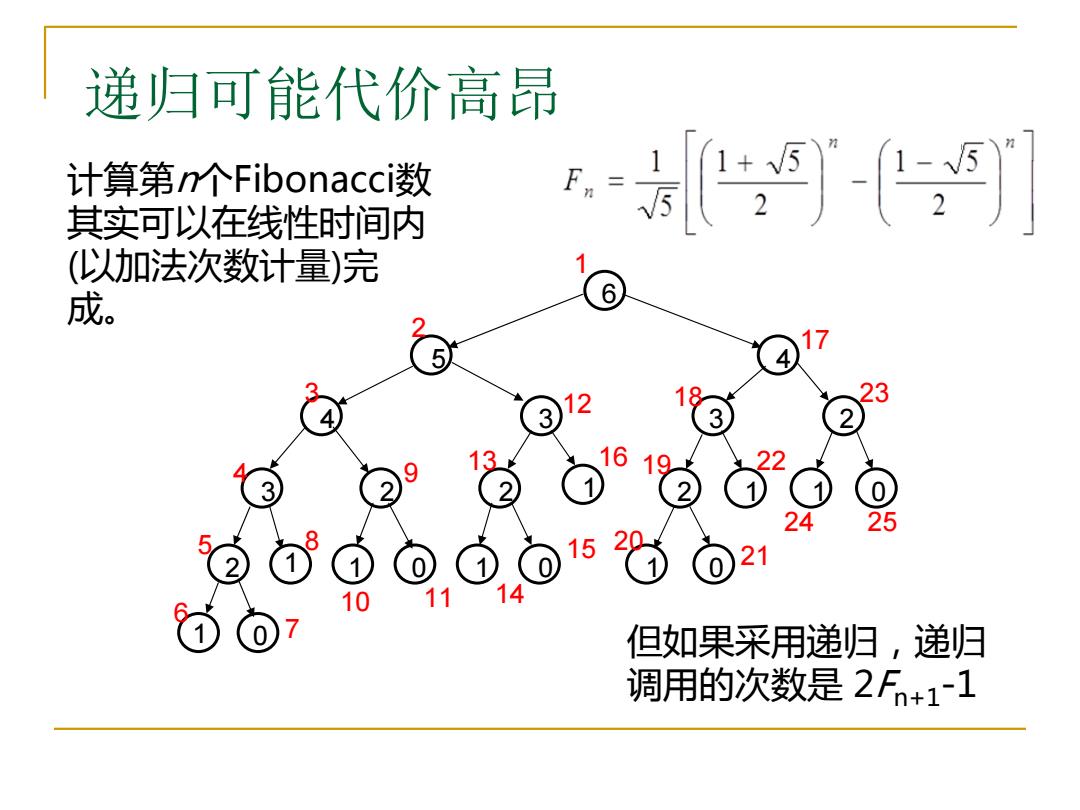
递归可能代价高昂 计算第n个Fibonacci数 其实可以在线性时间内 - (以加法次数计量)完 成。 6 17 5 2 8 3 3 9 0 24 25 15 21 但如果采用递割归,递归 调用的次数是2Fn+1~1
递归可能代价高昂 0 0 0 0 0 1 1 1 1 1 1 1 1 2 2 2 2 2 4 3 3 3 6 5 4 13 16 10 11 9 8 12 3 4 5 6 7 14 15 21 2 1 19 18 17 25 23 24 22 20 计算第 n个Fibonacci数 其实可以在线性时间内 (以加法次数计量)完 成。 但如果采用递归,递归 调用的次数是 2 Fn+1-1

问题2 相比较快速排序的分治法递 归,为什么上面的例子采用 递归代价高昂? QUICKSORT(A,p,r) 1 if p<r 2 g PARTITION(A,p,r) 3 QUICKSORT(A,p,q-1) 4 QUICKSORT(A,q+1,r)

问题3 我们有什么办法来应对这种 情况?

Rod Cutting Problem Therodnrob is the following.Given a rod of length ninches and a table of prices p for i=1,2,...ndetermine the maximum revenue obtain- able bytn up the od and selling the pieces. 一个样本输 入及其解: length i 1 2 3 4 5( 6789 10 price Pi 15 89101717202430 r=1 from solution 1 =1 (no cuts), r6 17 from solution 6=6 (no cuts), r2 5 from solution 2 =2 (no cuts), 7 18 from solution 7 =1+6 or 7=2+2+3, r3 =8 from solution 3=3 (no cuts), rs 22 from solution 8=2+6, r4 10 from solution 4=2+2, r9 25 from solution 9=3+6, rs 13 from solution 5=2+3, 1o =30 from solution 10=10 (no cuts)
Rod Cutting Problem 一个样本输 入及其解: r7 :

问题4: 为什么可能的割法数量 是2n-1?

间题5: 解决间题从那里开始? I: 我们总是要切第一刀的,但是 第一刀割在何2
我们总是要切第一刀的,但是 第一刀割在何? r7 :

递归的解法:扫描所有可能的割法 In max (Pn;rI+In-1,2 In-2,...,In-1+r1) Tn=maX(Pi十Tm-i) 1i蛇刀 间题6: CUT-ROD(p,n) 左边的两个式子 1 if0 2 return 0 有什么区别? 3 q=-0∞ 4 for i Iton 5 q max(q,p[i]+CUT-ROD(p,n-i)) 6 return q
递归的解法:扫描所有可能的割法

最优子结构: In max (Pn;rI In-1;r2 +In-2,...,In-1+r1) 问题7g 你能借助以上的式子解释一下 什么是最优子结构(Optimal Substructure)?
最优子结构: