
计算机问题求解一论题3-16 群与拉格郎日定理 2014年12月29日
计算机问题求解 – 论题3-16 - 群与拉格郎日定理 2014 年12 月29 日

下面的话是什么意思? It makes sense to write equations with group elements and group opera- tions.If a and b are two elements in a group G,does there exist an element EG such that ax =b?If such an x does exist,is it unique?The following proposition answers both of these questions positively
下面的话是什么意思?

问题1:什么是一个algebraic structures Table 3.1.Multiplication table for Zs 012345 67 0 0 0 0 0 0 0 0 0 1 2 4 5 6 7 23 0 2 4 6 0 2 4 6 0 3 6 1 4 7 2 5 4567 0 0 4 0 4 0 4 0 5 2 4 1 6 3 6 4 2 0 6 2 0 4 2 1 (Z8·)
问题1:什么是一个algebraic structures? (Z8,•)

Figure 3.2.Symmetries of a triangle B B identity id= B A B C 第二例: A B rotation A B B rotation A C B B reflection Table 3.2.Symmetries of an equilateral triangle 0 id P1 p2 μ1 2μ3 A B id id P1 p2 41 2 3 9 P1 B P2 id 3 1 2 B P2 id ps 2 3 1 reflection 1 2 3 id P2 2 2 3 P2 d A 3 山 2 id B A reflection = AB A C B
第二例:
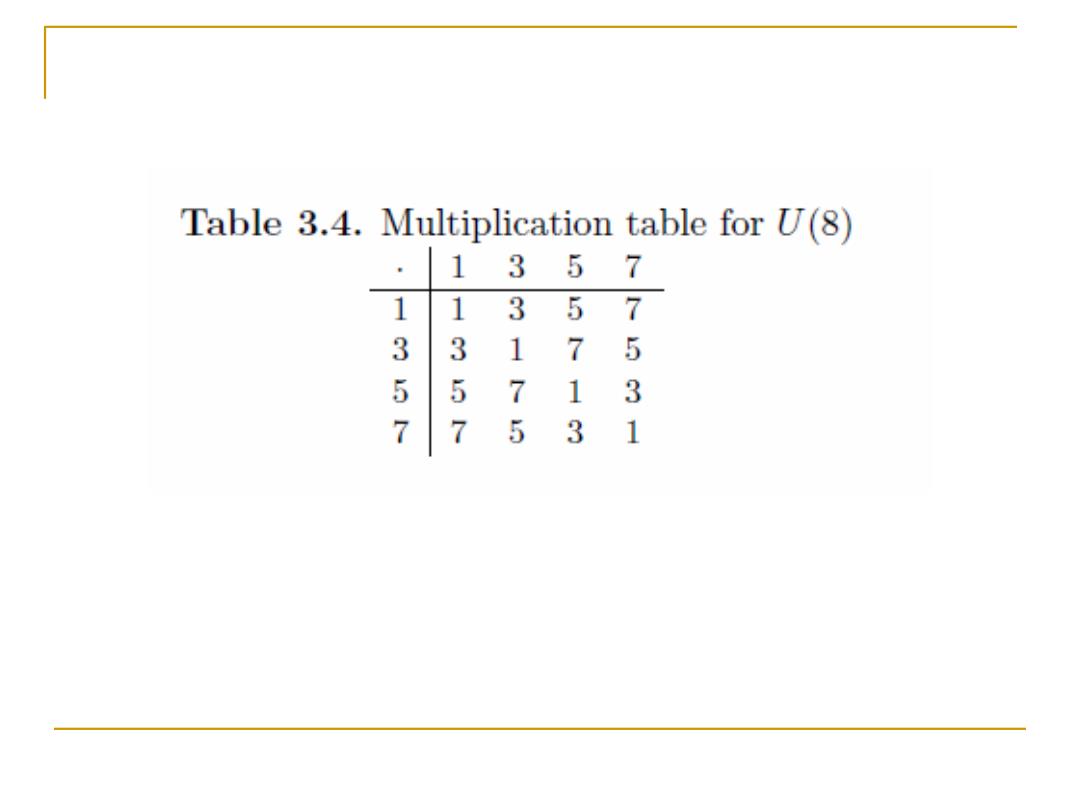
Table 3.4.Multiplication table for U(8) ·13 57 11357 1 75 5 71 3 人 5 3 1

一元一次方程的解 ■什么情况下,ax=b有解?解是否唯一?解是什 么? ■(R-0},×)具有什么性质?
一元一次方程的解 什么情况下,ax=b有解?解是否唯一?解是什 么? (R-{0}, × )具有什么性质?

群-一种“公理化”的代数系统 The law of composition is associative.That is, (aob)oc=ao(boc) fora,b,c∈G. There exists an element eE G,called the identity element,such that for any element a∈G eoa=aoe=a. For each element a e G,there exists an inverse element in G, denoted by a-1,such that aoa-1=a-loa=e. 注意:对于the integers mod n,加法一定构成群,乘法测未 必
群 – 一种“公理化”的代数系统 注意:对于theintegersmodn,加法一定构成群,乘法则未 必

问题 你还熟悉哪些“运算性 质”,在群公理中没有 提到?

问题: 群中有可能包含“0”吗?

问题 谈到群,你会联想到程 序设计语言中“数据类 型”的概念吗?