
计算机问题求解一论题2-10 排序与选择 2016年4月21日
计算机问题求解 – 论题2-10 - 排序与选择 2016年4月21日

问题1: 你能否利用下图解释快速排 序的基本思想? [splitPoint]:pivot [first灲 [last灯 0000O000000000 for any element in for any element in this Small large this segment,the key segment,the key is not is less than pivot. To be sorted recursively less than pivot
[first] [last] for any element in this segment, the key is less than pivot. for any element in this segment, the key is not less than pivot

QUICKSORT(A,p,r) 1 ifp<r 3 g PARTITION(A,p,r) 3 QUICKSORT(A,p,q-1) 4 QUICKSORT(A,q 1,r) To sort an entire array A,the initial call is QUICKSORT(A,1,A.length) 问题2: 都是用divide-and conquer策略,这与 Mergesort有什么不同?
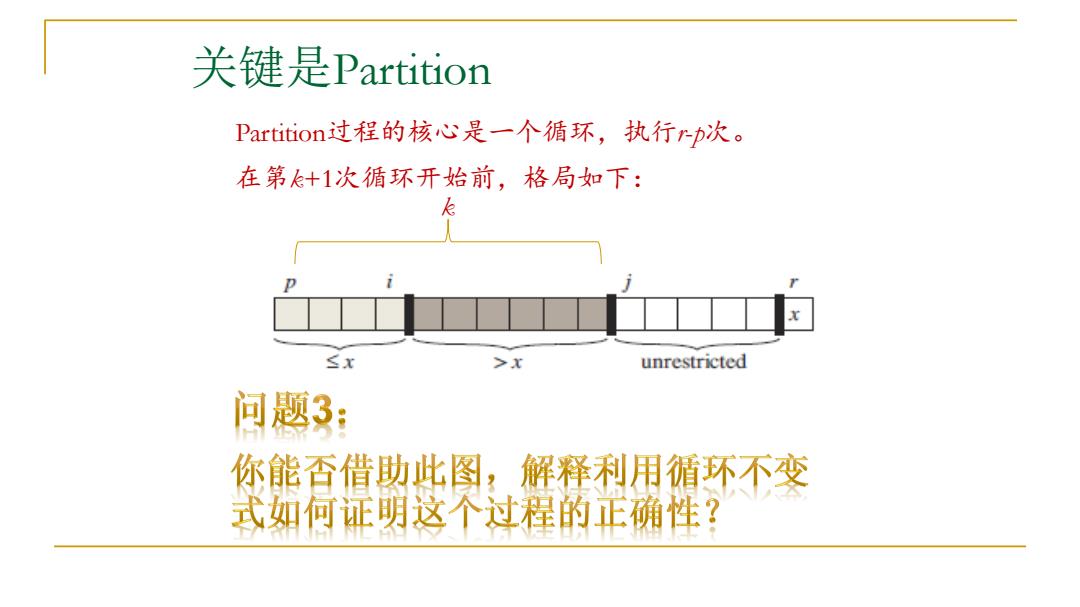
关键是Partition Partition过程的核心是一个循环,执行rp次。 在第飞+1次循环开始前,格局如下: k ≤x >x unrestricted 问题3: 你能否借助此图,解释利用循环不变 式如何证明这个过程的正确性?
关键是Partition Partition过程的核心是一个循环,执行r-p次。 在第k+1次循环开始前,格局如下: k

QUICKSORT(A,p,r) 1 ifp<r 2 g PARTITION(A,p,r) 3 QUICKSORT(A,p,q-1) 4 QUICKSORT(A,q+1,r) To sort an entire array A,the initial call is QUICKSORT(A,1,A.length) 问题4: 这个递归算法的时间性能递归式是什么?
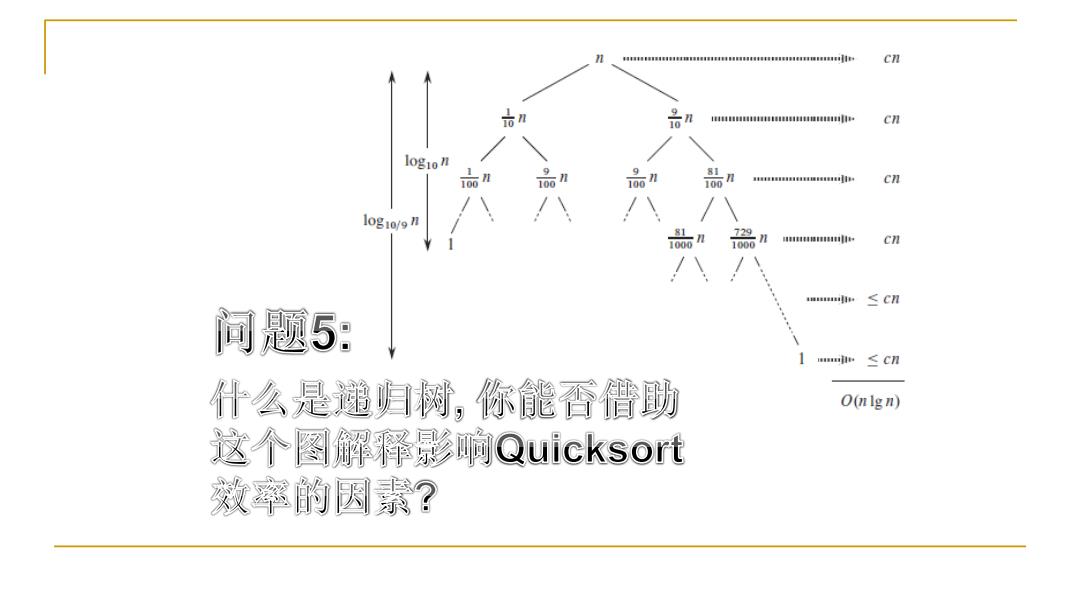
和体科用银可料 C刀 品n cn logion 品n 品n 银E接装料 cn 10g10/9n 品 n C刀 4aal≤C7 间题5: ≤C刀 什么是递归树,你能香借助 O(nlgn) 这个图解释影响Quicksort 效率的因素?

In fact,any split of constn proportionality yieldson te of depthhere the costateach lvel is O(m).The running time is therefore O(ng)whenever the split has constant roportionaty. 问题⑥; 你看了这句话有什么想法?

问题7: 为什台么直观上也会觉得快速排 序的平均效率更接近最好情况, 而不是最坏情况? 直觉对于探索很重要。 “大胆假设,小心求证!
直觉对于探索很重要。 “大胆假设,小心求证!

Worst-Case Performance of Quicksort T(m)=.max,(T(q)+T(-q-1)+Θ(m) 0sgs≤n-1 g是Partition的返回值。 问题8: 你能说说解这个递 归的策略吗? Guess and verifying
Worst-Case Performance of Quicksort q是Partition的返回值。 Guess and verifying

随机快速排序的期望代价 快速排序的主要代价其实就是Partition的代价。 ■Partition的代价主要是循环中的比较操作。 Lemma 7.1 Let X be the number of comparisons performed in line 4 of PARTITION over the entire execution of QUICKSORT on an n-element array.Then the running time of QUICKSORT is O(n+X). Proof By the discussion above,the algorithm makes at most n calls to PARTI- TION,each of which does a constant amount of work and then executes the for loop some number of times.Each iteration of the for loop executes line 4
随机快速排序的期望代价 快速排序的主要代价其实就是Partition的代价。 Partition的代价主要是循环中的比较操作