
计算机问题求解一论题3-6 -图的计算机表示以及遍历 2016年10月08日
计算机问题求解 – 论题3-6 -图的计算机表示以及遍历 2016年10月08日
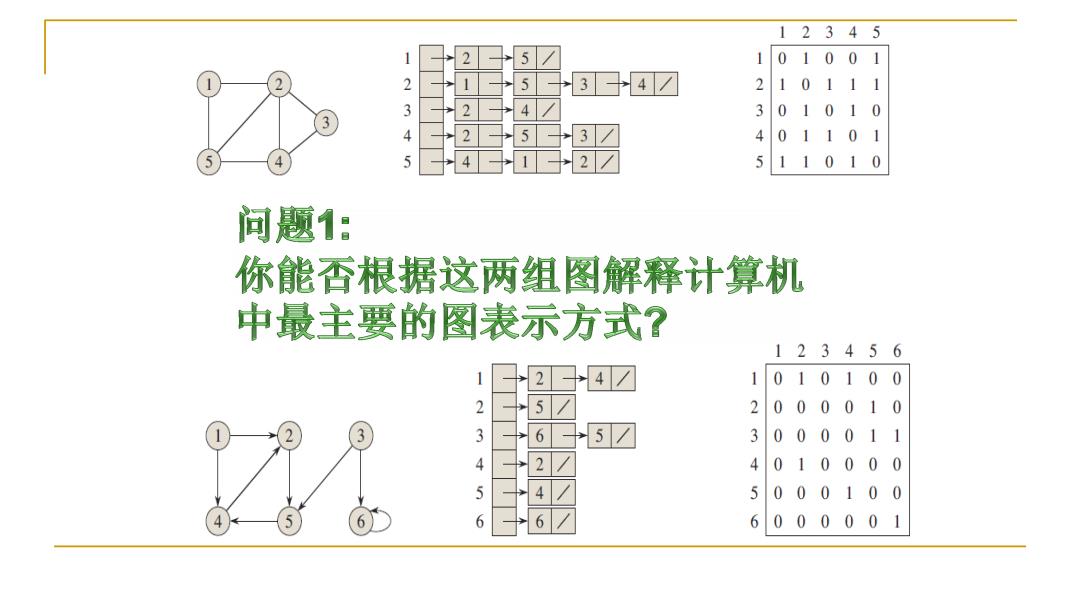
12345 01001 3 4☑ 1 0111 3 01010 3 01101 5 11010 问题1: 你能否根据这两组图解释计算机 中最主要的图表示方式? 123456 4☑ 1010100 2 2000010 3 3 5☑ 3 000011 4 4010000 5 0001 00 6 6 6 000001

问题2: 我们讨论表示方法是否合 适主要根据什么? 你能否结合上述两种方式 给以说明? 关键操作的效率vS.存储需求
关键操作的效率 vs. 存储需求

问题3: 通常图中与应用相关的附加 信息有些什么?他们对表示 方法的选择有什么影响?

问题4: 图的搜索是什么意思? 为什么它是用图模型解 决问题的基本操作? 图搜索经常被称为"遍历”(raversal)
图搜索经常被称为“遍历”(traversal)
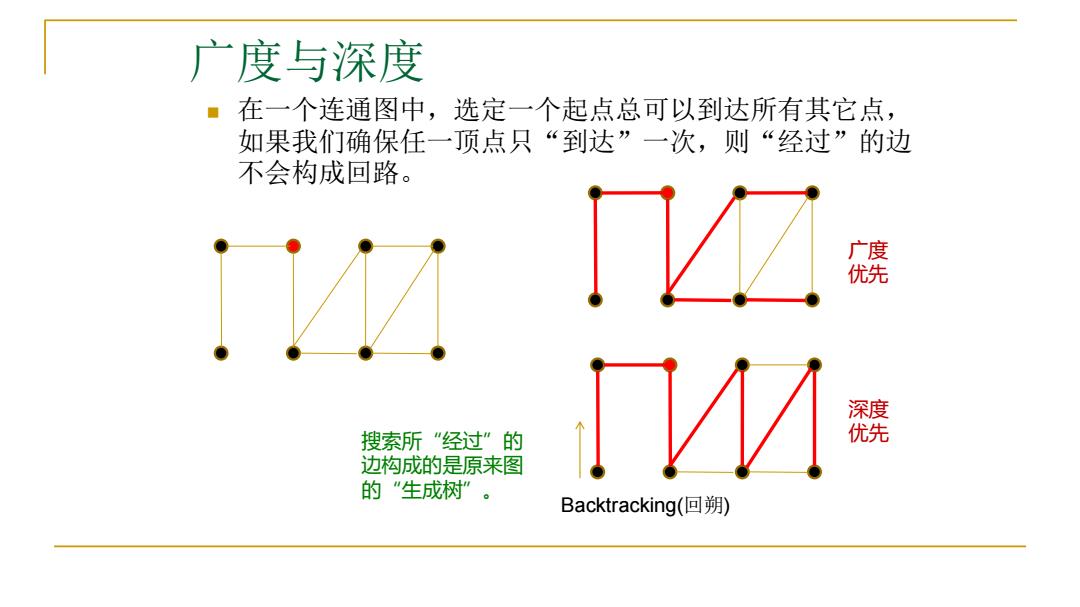
广度与深度 ■在一个连通图中,选定一个起点总可以到达所有其它点, 如果我们确保任一顶点只“到达”一次,则“经过”的边 不会构成回路。 广度 优先 深度 搜索所“经过”的 V 优先 边构成的是原来图 的"生成树”。 Backtracking(▣朔)
在一个连通图中,选定一个起点总可以到达所有其它点, 如果我们确保任一顶点只“到达”一次,则“经过”的边 不会构成回路。 广度与深度 搜索所“经过”的 边构成的是原来图 的“生成树”。 Backtracking(回朔) 广度 优先 深度 优先

广度优先 Given a graph G=(V,E)and a distinguished source vertex s,breadth-first search systematically explores the edges of Gto"discover"every vertex that is reachable from s.It computes the distance (smallest number of edges)from s to each reachable vertex.It also produces a"breadth-first tree"with root s that contains all reachable vertices.For any vertexrechable froms,the simple path in the breadth-first tree from s to corresponds to a"shortest path"from s tov in G,that is,a path containing the smallest number of edges.The algorithm works on both directed and undirected graphs. 两个关键的动词
广度优先 两个关键的动词

问题5: 图搜索时用什么办法来跟 踪搜索的进度?

BFS(G,s) b 0w7 1 for each vertex u G.V-{s} 2 u.color=WHITE 3 u.d =oo 4 u,π=NIL Q r t x d Q r x v 5 s.color GRAY 122 222 6s.d=0 7S.π=NIL 8 Q=0 ①0 1 0 3 ENQUEUE(O,s) 2 x v a (0 0u3 10 223 while O≠0 2 233 11 WDEQUEUE(O) 12 forleach v E G.Adilu] 10 3 13 if v.color =WHITE Q M y 14 v.color GRAY 2 33 2 3 15 v.d u.d+1 16 .π=2M 问题6: 17 ENQUEUE(O,v) 1 u.color BLACK 在何处体现”frontier expansion”? 为什么“扩张”的结果一定是树?

BFS(G,s) 1 for each vertex u G.V-{s} 2 u.color=WHⅡTE 问题7: 3 u.d =oo 4 u.π=NL S.color GRAY 为什么说广度优 6 s.d=0 7 S.π=NIL 先搜索的代价是 8 Q=0 9 ENQUEUE(O,s) 线性的?其问题 10 while O≠0 11 DEQUEUE(O) 规模是用什么参 12 for each v∈G.Adju 13 if v.color =WHITE 数表示的? 14 v.color GRAY 15 v.d u.d+1 16 y.π=u 17 ENQUEUE(O,v) 18 u.color BLACK