
计算机问题求解-论题3-11 图中的匹配与因子分解 2016-11-23
计算机问题求解---论题3-11 图中的匹配与因子分解 2016-11-23

要在左图所示的棋盘上放 × 置4个士兵,任何一行或者 一列恰好放一个,但不能 X 放在有标记的格子中。 × × 问题1: × 你能建一个图 模型来解这样 的问题吗?
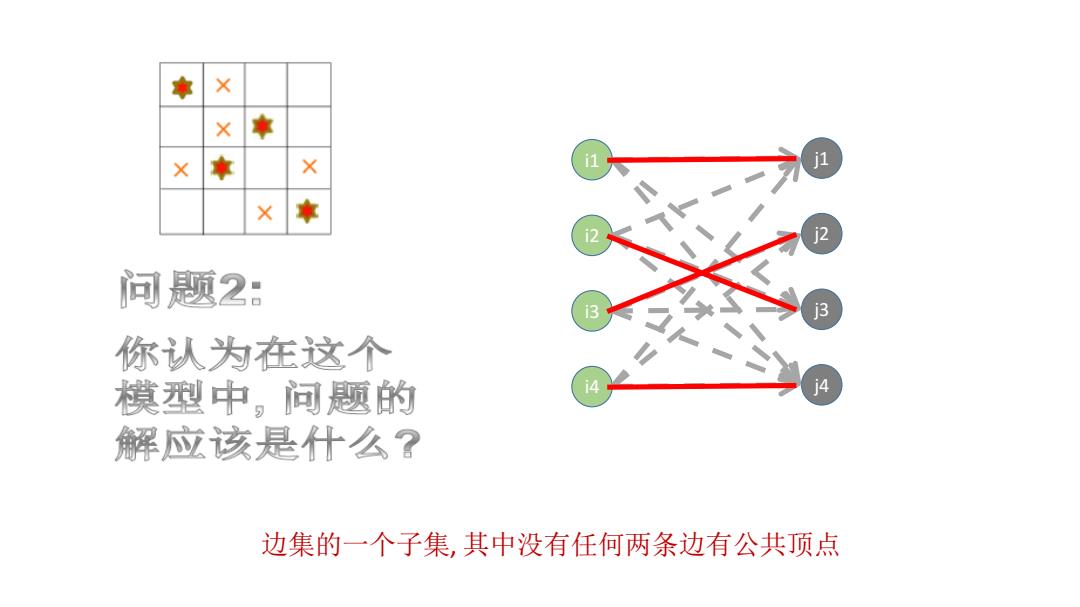
X X 问题2: 你认为在这个 模型中。问题的 解应该是什么? 边集的一个子集,其中没有任何两条边有公共顶点
i1 i2 i3 i4 j1 j2 j3 j4 边集的一个子集, 其中没有任何两条边有公共顶点

什么是matching? d 8 A B D E (a) (b) Figure 8.2:A matching in a bipartite graph 独立边集是匹配的核心概念。问题3:你能用集 合论里面的基本概念解释matching吗?极大匹配? 完美匹配?
什么是matching? 独立边集是匹配的核心概念。问题3:你能用集 合论里面的基本概念解释matching吗?极大匹配? 完美匹配?

匹配、极大匹配、最大匹配、完美匹配 e e e3 e e2 e e es e es )6 6 6
匹配、极大匹配、最大匹配、完美匹配 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5

二部图中最大匹配的存在性 Theorem 8.3 Let G be a bipartite graph with partite sets U and W such that r Us W.Then G contains a matching of cardinality r if and only if G satisfies Hall's condition. 必要性: G B D F K L M
二部图中最大匹配的存在性 必要性:

Theorem 8.3 Let G be a bipartite graph with partite sets U and W such that r =Us W.Then G contains a matching of cardinality r if and only if G satisfies Hall's condition. ·充分性 ·奠基:|U川=1,显然 你能想到用数学 归纳法证明吗? ·假设:IU≤Wand1≤IUIS引,是成立的。否则,很难看出 现在你能理解为什么在归纳证明中,需要分情形证明了吗?
• 充分性 • 奠基: |U|=1,显然 • 假设: 结论成立 • 归纳证明要点: • 从U任取一个u,从N(u)中任取一个w,构造H:G-{u,w}:H满足Hall条件吗? • 如果对U的任意子集S,|N(S)|>|S|,是成立的。否则,很难看出 你能想到用数学 归纳法证明吗? 现在你能理解为什么在归纳证明中,需要分情形证明了吗?

Case 2.There exists a proper subset X ofU such that N(X)=X.Let F be the bipartite subgraph of G with partite sets X and N(X).Since Hall's condition is satisfied in F,it follows by the induction hypothesis that X can be matched to a subset of N(X).Indeed,since N(X)=X],the set X can be matched to N(X).Let M'be such a matching. Next,consider the bipartite subgraph H of G with partite sets U-X and W-N(X).Let S be a subset of U-X and let S'=N(S)n(W-N(X)). We show that |Ss S'l.By assumption,N(XUS)XUS.Hence N(X)川+ISI=lN(XUS)I≥X|+S

这个定理的直观含义是什么? Theorem 8.4 A collection {S S2,...S of nonempty finite sets has a system of distinct representatives if and only if for each integer k with 1 s k s n,the union of any k of these sets contains at least k elements. For example,consider the sets S,S,...S,where S1={1,2,3}S2={2,4,6} S3={3,4,5} S4={1,4,7} S5={1,5,6} S6={3,6,7} S7={2,5,7} Then this collection of sets has a system of distinct representatives.In particular,1,2,.... 7(that is,i S;for i=1,2,...,7)is a system of distinct representatives.On the other hand,the setswhere S1={1,3,5,6}S%={3,4} S3={4,5} S4={3,4,5} Sg={1,2,4,6}S%={3,5}, do not have a system of distinct representatives as S2UUUS={3,4,5 so distinct representatives do not exist for the sets
这个定理的直观含义是什么?
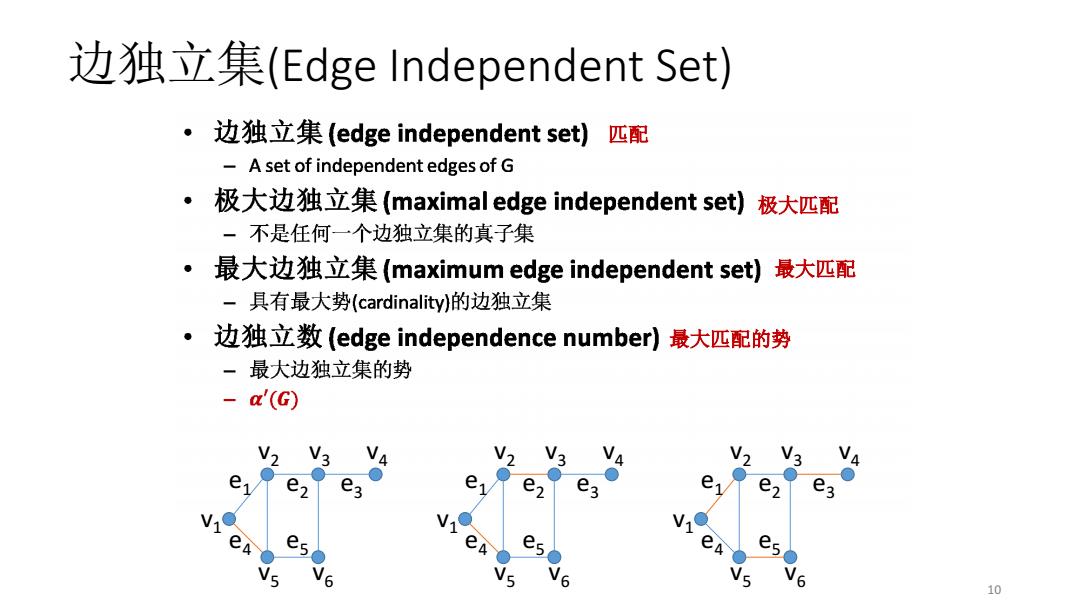
边独立集(Edge Independent Set) ·边独立集(edge independent set)匹配 A set of independent edges of G 。 极大边独立集(maximal edge independent set)极大匹配 一不是任何一个边独立集的真子集 ·最大边独立集(maximum edge independent set)最大匹配 -具有最大势(cardinality)的边独立集 · 边独立数(edge independence number)最大匹配的势 一最大边独立集的势 -a'(G) V2 V e1 e V e es 10
边独立集(Edge Independent Set) 10 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 匹配 极大匹配 最大匹配 最大匹配的势