
计算机问题求解一论题4.8 优化问题的近似解 陶先平 2017年5月8日
计算机问题求解—论题4.8 优化问题的近似解 陶先平 2017年5月8日

生产调度问题的一个近似解 Algorithm 4.2.1.3 (GMS (GREEDY MAKESPAN SCHEDULE)). Input:I=(p1,...,Pn,m),n,m,p1,...,Pn positive integers and m2. Step 1:Sort p1,...,Pn. To simplify the notation we assume p1≥p2≥.≥pn in the rest of the algorithm. Step 2:for i=1 to m do begin Ta={); Time(T:):=Pi end [In the initialization step the m largest jobs are distributed to the m machines.At the end,Ti should contain the indices of all jobs assigned to the ith machine for i=1,...,m.} Step 3:for i=m+1 to n do begin compute an I such that Time(T):=min{Time(Til1≤j≤m T:=nUi): Time(T):=Time(Ti)+pi end Output:(T1,T2,...,Tm)
生产调度问题的一个近似解
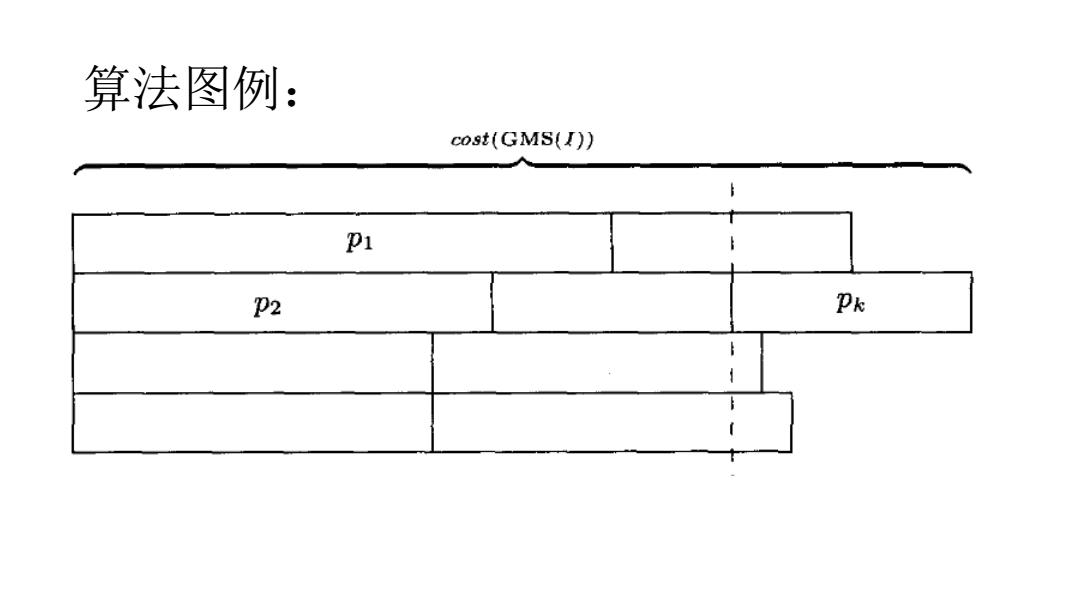
算法图例: cost(GMS(I)) P1 P2 Pk
算法图例:

这段文字中的quality是什么意思? mally and roughly,an approximation algorithm for an optimization problem is an algorithm that provides a feasible solution whose quality does not differ too much from the quality of an optimal solution. 这个公式中的cost是什么意思? EA(x)= cost(A(x))-Optu(x Optu(x)
这段文字中的quality是什么意思? 这个公式中的cost是什么意思?

问题1 n代表什么意思? For any n E N,we define the relative error of A as eA(n)=max{EA(x)x∈Lr∩(∑r)"}. For every x E LI,the approximation ratio RA(x)of A on x is defined as aa=mr{智a}-
问题1 n代表什么意思?

我们希望能够得到某个近似算法的如下结论: For any positive real 6>1,we say that A is a 6-approximation algo- rithm for U if RA(x)≤6 for every x∈LI. 如果不能,我们要努力得到某个近似算法的这个结论: For every function f:N-R+,we say that A is an f(n)-approximation algorithm for U if RA(n)≤f(n)for every n∈N
我们希望能够得到某个近似算法的如下结论: 如果不能,我们要努力得到某个近似算法的这个结论:

生产调度问题的一个近似解 Algorithm 4.2.1.3 (GMS (GREEDY MAKESPAN SCHEDULE)). Input:I=(p1,...,pn,m),n,m,p1,...,p ositive integers and m 2. Step 1:Sort p1,...,Pn. To simplify the nota 2p2≥T≥pn in the rest of th hm. Step 2: for i 这个算法会 差到什么程 edistributed to the 度呢? dices of all jobs ,m.} 40 b compce an I such that me(T):=min{Time(T,)1≤j≤m}; T:=TU{}: Time(T):=Time(Ti)+pi end Output:(T,T2,.,Tm)为
生产调度问题的一个近似解 这个算法会 差到什么程 度呢?

GMS算法的误差分析中的几个概念: OptMS(I)≥p1≥p2≥·≥pn: Clearly, OptMs(I)≥ ∑21p 4.2 m 我们不知道MS的最优解是什么, 但是我们总是可以给出最优解的 Pk≤ ∑1卫 某些性质,依据这些性质,可以 k 4.3 讨论具体这个算法的解和最优解 之间的差距
GMS算法的误差分析中的几个概念: 4.2 我们不知道MS的最优解是什么, 但是我们总是可以给出最优解的 某些性质,依据这些性质,可以 讨论具体这个算法的解和最优解 之间的差距 4.3

证明概要: ·分情形证明: 。nm. Let Ti be such that cost(T)=reTPr=cost(GMS(I)),and let k be the largest index in Ti.If k m,then T=1 and so Optms(I)=p1 =pk and GMS(I)is an optimal solution. Now,assume mcost(GMS(I))-pk (4.4) because of∑p:≥m·[cost(GMS(I)-pkl and(4.2 为什么?
证明概要: • 分情形证明: • n <= m • 第一个任务的时间长度是最优解 为什么?

Combining the inequalities (4.3)and (4.4)we obtain cost(GMS(I)-OptMs(I)≤pk≤ (4.4) (4.3) (/ =1 Finally,we bound the relative error by the following calculation: cost(GMS(I))-OptMs(I) (∑1)/k m ≤ OptMS(I) (4.5)】 (∑1p)/m (4.2) 到此为什么就可以说GMS算法是MS问题的2近似算法?
到此为什么就可以说GMS算法是MS问题的2近似算法?