
问题求解论题1-9 关系 2017年11月30日
问题求解论题1-9 关系 2017年11月30日

有序偶的集合表示形式 问题1:“有序”的有序偶表达需求该如何用“无 序”的集合这样的数学模型来建模? (a,b)的集合表现形式是? {a,{a,b}
有序偶的集合表示形式 问题1: “有序”的有序偶表达需求该如何用“无 序”的集合这样的数学模型来建模? 𝑎, 𝑏 的集合表现形式是? 𝑎, 𝑎, 𝑏

二元关系的论域(universe) The set of all possible objects that are considered in the context in which we work is called the universe. 问题2:就二元关系R二A×B而言,其论域是什么? 通常情况下,我们讨论A=B的一类特殊关系较多 "S is a relation on a set x"is one way of saying that S is a subset of X×X
二元关系的论域(universe) 问题2:就二元关系𝑹 ⊆ 𝑨 × 𝑩而言,其论域是什么? 通常情况下,我们讨论A=B的一类特殊关系较多 “S is a relation on a set 𝑿” is one way of saying that S is a subset of 𝑿 × 𝑿 The set of all possible objects that are considered in the context in which we work is called the universe
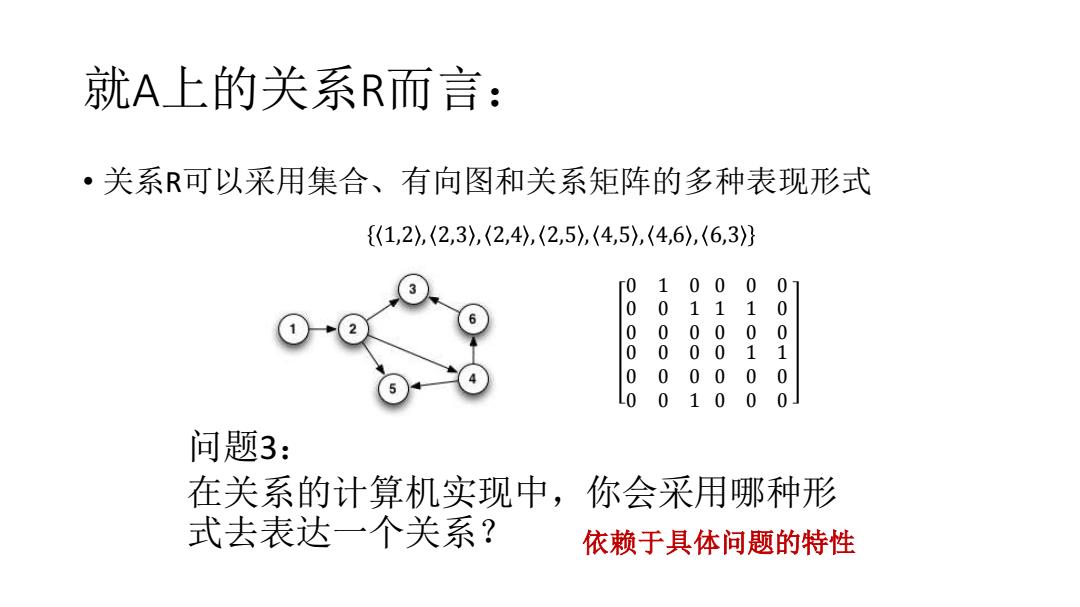
就A上的关系R而言: ·关系可以采用集合、有向图和关系矩阵的多种表现形式 {(1,2),(2,3),(2,4),(2,5),(4,5),(4,6),(6,3)} ro 1000 01 0 0111 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 010 0 问题3: 在关系的计算机实现中,你会采用哪种形 式去表达一个关系? 依赖于具体问题的特性
就A上的关系R而言: • 关系R可以采用集合、有向图和关系矩阵的多种表现形式 问题3: 在关系的计算机实现中,你会采用哪种形 式去表达一个关系? 1,2 , 2,3 , 2,4 , 2,5 , 4,5 , 4,6 , 6,3 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0 依赖于具体问题的特性

问题4: 你觉得下面的表示“奇怪”吗? 口自然数集合上:“”=中 问题5:你如何理解、区分上述式子中的“=”和=?
问题4: 问题5:你如何理解、区分上述式子中的“=”和=?

关系的“复合”运算 ·关系的“复合”运算 ·运算法则: 如果R1∈A×B,R2SB×C 则:R1与R2的复合关系R1。R2∈A×C定义为 R1R2 ={(x,z川xEA,z∈C,and3y ∈B,S.t.(x,y〉∈R1,(y,z〉ER2}
关系的“复合”运算 •关系的“复合”运算 • 运算法则: 如果𝑅1 ⊆ 𝐴 × 𝐵, 𝑅2 ⊆ 𝐵 × 𝐶 则:𝑅1与𝑅2的复合关系𝑅1 ∘ 𝑅2 ⊆ 𝐴 × 𝐶定义为 𝑅1 ∘ 𝑅2 = ሼ ሽ 𝑥, 𝑧 |𝑥 ∈ 𝐴, 𝑧 ∈ 𝐶, 𝑎𝑛𝑑 ∃𝑦 ∈ 𝐵, 𝑠.𝑡. 𝑥, 𝑦 ∈ 𝑅1 , 𝑦, 𝑧 ∈ 𝑅2
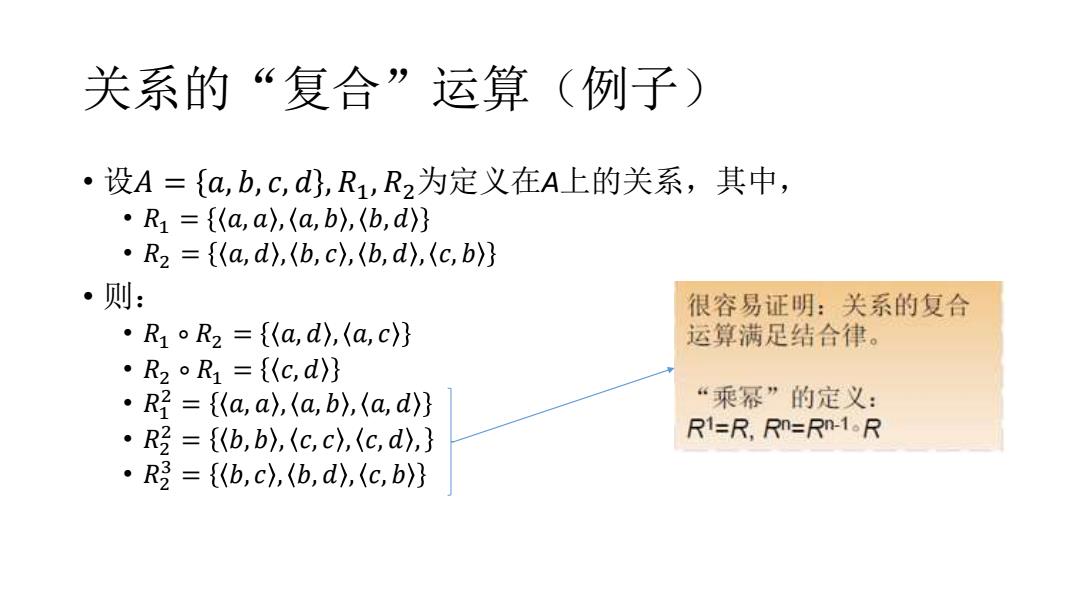
关系的“复合”运算(例子) ·设A={ab,C,d,R1,R2为定义在A上的关系,其中, ·R1={(a,a),(a,b),(b,d)} ·R2={(a,d),(b,c),(b,d),(c,b)} ·则: 很容易证明:关系的复合 ·R1oR2={(a,d),(a,c)} 运算满足结合律。 ·R2oR1={(c,d} ·R={a,a),(a,b,(a,d)} “乘幂”的定义: ·R3={《b,b),(c,c,(c,d,} R1=R.Rn=RD-1R ·R={b,c,(b,d),(c,b)}
关系的“复合”运算(例子) • 设𝐴 = 𝑎, 𝑏, 𝑐, 𝑑 , 𝑅1 , 𝑅2为定义在A上的关系,其中, • 𝑅1 = 𝑎, 𝑎 , 𝑎, 𝑏 , 𝑏,𝑑 • 𝑅2 = 𝑎, 𝑑 , 𝑏, 𝑐 , 𝑏, 𝑑 , 𝑐, 𝑏 • 则: • 𝑅1 ∘ 𝑅2 = 𝑎, 𝑑 , 𝑎, 𝑐 • 𝑅2 ∘ 𝑅1 = 𝑐, 𝑑 • 𝑅1 2 = 𝑎, 𝑎 , 𝑎, 𝑏 , 𝑎, 𝑑 • 𝑅2 2 = 𝑏, 𝑏 , 𝑐, 𝑐 , 𝑐, 𝑑 , • 𝑅2 3 = 𝑏, 𝑐 , 𝑏, 𝑑 , 𝑐, 𝑏

问题6: 关系可以用矩阵和图来表示,关系的复合 运算在这两种表现形式下,如何解读? R1={a,a〉,(a,b,(b,d)} [1 10 01 1 0 010 00 0 1 0 0 1 00 0 = 000 0 0 0 0 0 0 1 0 0 0 0 o 100 1100 1000 0 00 0 0 0 0 R2={《a,d),(b,c,(b,d),(c,b)} R1oR2={(a,d),(a,c} 0 0 0 1100 00
问题6: 关系可以用矩阵和图来表示,关系的复合 运算在这两种表现形式下,如何解读? 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 𝑅1 = 𝑎, 𝑎 , 𝑎, 𝑏 , 𝑏, 𝑑 0 0 0 0 0 1 1 1 0 1 0 0 0 0 0 0 𝑅2 = 𝑎, 𝑑 , 𝑏, 𝑐 , 𝑏, 𝑑 , 𝑐, 𝑏 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 × 0 0 0 0 0 1 1 1 0 1 0 0 0 0 0 0 = 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 𝑅1 ∘ 𝑅2 = 𝑎, 𝑑 , 𝑎, 𝑐
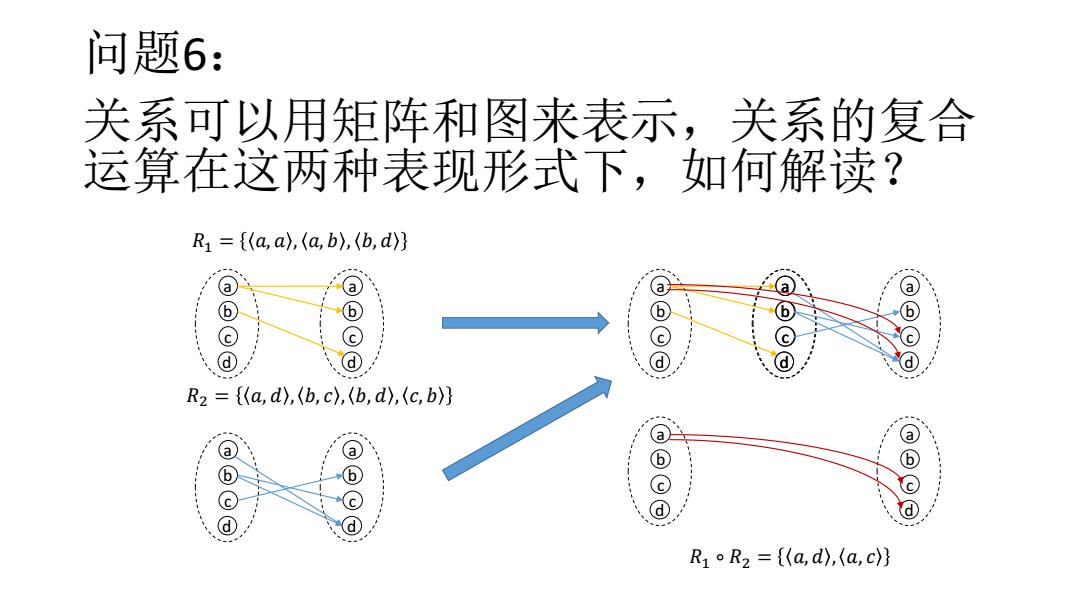
问题6: 关系可以用矩阵和图来表示,关系的复合 运算在这两种表现形式下,如何解读? R1={(aa),(a,b),(b,d)} a a a oC ⊙ @ 。@ d d R2={(a,d),(b,c),(b,d),(c,b} a ③ ⑤@@ R1oR2={(a,d),(a,c)}
问题6: 关系可以用矩阵和图来表示,关系的复合 运算在这两种表现形式下,如何解读? 𝑅1 = 𝑎, 𝑎 , 𝑎, 𝑏 , 𝑏, 𝑑 𝑅2 = 𝑎, 𝑑 , 𝑏, 𝑐 , 𝑏, 𝑑 , 𝑐, 𝑏 a b c d a b c d a b c d a b c d a b c d a b c d a b c d a b c d a b c d 𝑅1 ∘ 𝑅2 = 𝑎, 𝑑 , 𝑎, 𝑐

问题6: 关系可以用矩阵和图来表示,关系的复合 运算在这两种表现形式下,如何解读? R1={(a,a),(a,b),(b,d)} r=(a,a,(a,b>,(ad)} b
问题6: 关系可以用矩阵和图来表示,关系的复合 运算在这两种表现形式下,如何解读? 𝑅1 = 𝑎, 𝑎 , 𝑎, 𝑏 , 𝑏, 𝑑 a b c d a b c d 𝑅1 2 = 𝑎, 𝑎 , 𝑎, 𝑏 , 𝑎, 𝑑