
计算机问题龙解一论题1-11 有限与无限 2017年12月14日
计算机问题求解 – 论题1-11 - 有限与无限 2017年12月14日

“聪明的经理”、“非常聪明的经理” 和“非常非常聪明的经理” 问题1: 你能给我们讲讲这个故事吗? WELCOME TO HILBERTS HOTEL-INFINITE PLEASURES.INFINITE STAYS 00 满 “希尔伯特旅馆” http://www.science4all.org/article/cantors-infinite/
客 满 “聪明的经理” 、 “非常聪明的经理” 和“非常非常聪明的经理” “希尔伯特旅馆” http://www.science4all.org/article/cantors-infinite/

集合的等势 To make precise what it means for two sets (even two infinite sets)to have the same number of elements,we need a definition. We say that a set A is equivalent to a set B if there exists a bijection f:AB.We write A B for A is equivalent to B.(Other authors use the words equipotent or equinumerous. 问题2: 你原来脑海中的两个集合元素一样多”的概 念是什么样的呢? 对无穷集合遁用吗?
集合的等势

问题3:如何精确定义什么是有限集? We say that a set Sis finite ifeither =or ifs is equivalent to the set(1,23,... for sme positive inteer. 更加数学化的表述:(每一个自然数也是一个集合) 空集记为0; 如果是自然数,则其“后继”为:k心3。 于是 有限集就是与某个自然数等势的集合
问题3:如何精确定义什么是有限集? 更加数学化的表述:(每一个自然数也是一个集合) 空集记为0; 如果k是自然数,则其“后继”为: k {k} 。 于是: 有限集就是与某个自然数等势的集合

问题4: 什么是无限集合? 提示:有限集就是与某个自然数等势的集合 A set is infinite if it is not finite A set is infinite if and only if for every natural number the set has a subset whose cardinality is that natural number
提示:有限集就是与某个自然数等势的集合 A set is infinite if and only if for every natural number the set has a subset whose cardinality is that natural number. A set is infinite if it is not finite
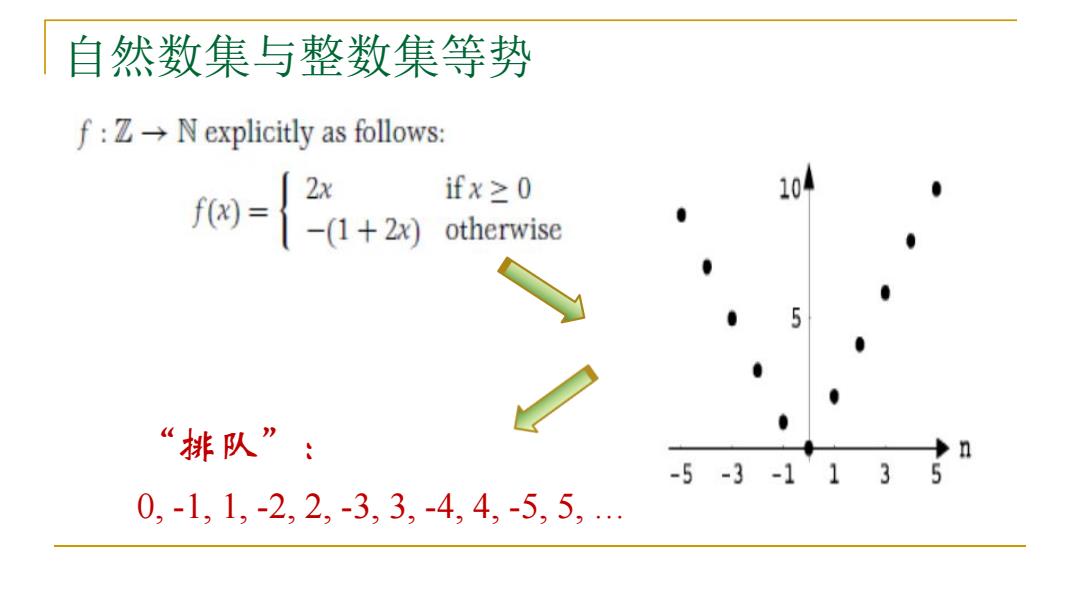
自然数集与整数集等势 f:ZN explicitly as follows: 0-+2对 ifx≥0 104 otherwise “排队”: n -5-3-1135 0,-1,1,-2,2,-3,3,-4,4,-5,5,…
自然数集与整数集等势 “排队” : 0, -1, 1, -2, 2, -3, 3, -4, 4, -5, 5, …

问题5: 6.a-3,-2,-1,0,12,3,9不 能算排好队了,为什么?

关于双射的证明(1) f:ZN explicitly as follows: 注意: 2x f=1 ifx≥0 不能遗漏了case3! -(1+2x)otherwise Proof that f is one-to-one. Letm,n∈Z and suppose that f(m)≠f(n). Case 1.Suppose that m0 and n z0.Then f(m)=2m and f(n)=2n.Thus 2ni =2n,and therefore m=n. Case 2.Suppose that m<0 and n 0.Then f(m)=-2m-1 and f(n)=-2n-1.Thus,-2m-1 =-2n-1,and therefore m =n. Case 3.S Suppose that one of the two,say m,is nonnegative,and the other is negative.Then f(m)=2m and f(n)=-2n-1. Thus 2m =-2n-1.But this means that an even number, 2m,is equal to an odd number,-2n-1,which is impossible. Therefore,if f(m)=f(n),only case 1 and case 2 can occur.In either of these cases,we have shown that m =n.Thus f is one-to- one. ■
关于双射的证明 (1) 注意: 不能遗漏了case 3!

关于双射的证明(2) f:ZN explicitly as follows: f-{2+2 2x ifx≥0 otherwise Proof that f maps Z onto N. Letk∈N.If k is even,then k=2 m for some m∈Z with m≥O. Thus,m eZ and f(m)=2m k.If k is odd,then k+1 is even. Hence m=(k+1)/(-2)∈Z.Since k≥1,we have m<0.Thus, f(m)=-2m-1 =-2((k +1)/(-2))-1 k.We conclude that for allk∈N,there exists m∈Z such that f(m)=k.Sincef:Z→Nis a well-defined function,f maps Z onto N. ■
关于双射的证明 (2)

无穷不仅仅是“很多很多 Not necessary It is possible to define comparisons 伽利略悖论: amongst infinite sets in a meaningful way! 整体与局部“一样大”】 23 4 5 67 8 Galileo Galilei 1625 36 49 64.. The ideas of less,equal,and greater apply to (what we would now call)finite sets,but not to infinite sets https://en.wikipedia.org/wiki/Galileo%27s paradox
无穷不仅仅是“很多很多” 伽利略悖论: 整体与局部“ 一样大”! https://en.wikipedia.org/wiki/Galileo%27s_paradox Galileo Galilei The ideas of less, equal, and greater apply to (what we would now call) finite sets, but not to infinite sets! Not necessary! It is possible to define comparisons amongst infinite sets in a meaningful way!