
计算机问题求解-论题3.3 图的基本概念 陶先平 2018年9月25日
计算机问题求解 -论题 3.3 图的基本概念 陶先平 2018年9月25日
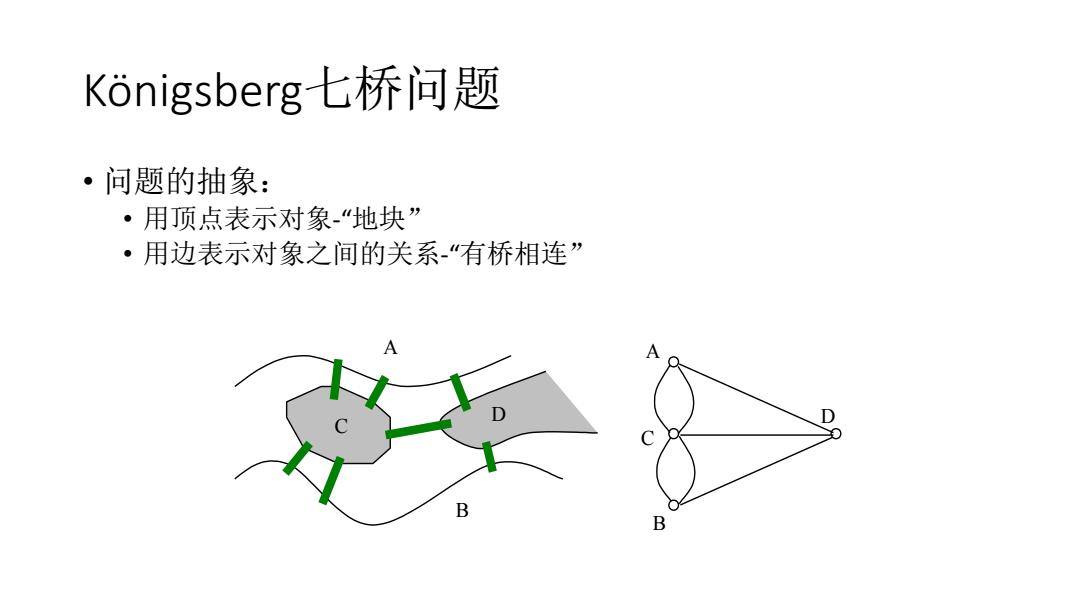
Konigsberg-七桥问题 ·问题的抽象: ·用顶点表示对象-“地块” ·用边表示对象之间的关系“有桥相连” D B B
Königsberg七桥问题 • 问题的抽象: • 用顶点表示对象-“地块” • 用边表示对象之间的关系-“有桥相连” C D A B A C B D

“巧渡河”问题 ·问题:人、狼、羊、菜用一条只能同时载两位的小船渡河,“狼羊”、 “羊菜”不能在无人在场时共处,当然只有人能架船。 ·图模型:顶点表示“原岸的状态”,两点之间有边当且仅当一次合理 的渡河“操作”能够实现该状态的转变。 ·起始状态是“人狼羊菜”,结束状态是“空”。 ·问题的解:找到一条从起始状态到结束状态的尽可能短的通路
“巧渡河”问题 • 问题:人、狼、羊、菜用一条只能同时载两位的小船渡河,“狼羊”、 “羊菜”不能在无人在场时共处,当然只有人能架船。 • 图模型:顶点表示“原岸的状态”,两点之间有边当且仅当一次合理 的渡河“操作”能够实现该状态的转变。 • 起始状态是“人狼羊菜”,结束状态是“空”。 • 问题的解:找到一条从起始状态到结束状态的尽可能短的通路
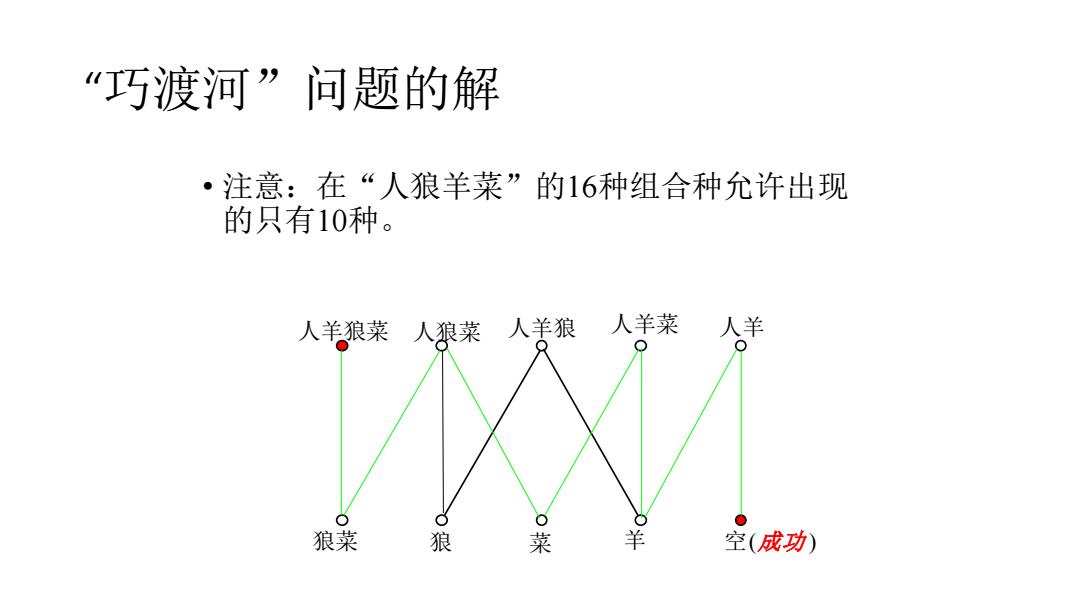
“巧渡河”问题的解 ·注意:在“人狼羊菜”的16种组合种允许出现 的只有10种。 人羊狼菜人狼菜人羊狼人羊菜人羊 狼菜 狼 菜 羊 空(成功)
“巧渡河”问题的解 • 注意:在“人狼羊菜”的16种组合种允许出现 的只有10种。 空(成功 ) 人羊狼菜 人狼菜 人羊狼 人羊菜 狼菜 狼 菜 人羊 羊

考试时间编排问题 ·问题:排考试时间,一方面要总时间尽可能短(假设教室没问题), 一方面一个同学所选的任意两门课不能同时间。 ·图模型:每门课程对应一个顶点。任意两点相邻当且仅当对应的两门 课程有相同的选课人。 ·解:用不同颜色给顶点着色。相邻的点不能同颜色。则最少着色数即 至少需要的考试时间段数(可以将颜色相同的点所对应的课程安排在 同一时间)
考试时间编排问题 • 问题:排考试时间,一方面要总时间尽可能短(假设教室没问题),另 一方面一个同学所选的任意两门课不能同时间。 • 图模型:每门课程对应一个顶点。任意两点相邻当且仅当对应的两门 课程有相同的选课人。 • 解:用不同颜色给顶点着色。相邻的点不能同颜色。则最少着色数即 至少需要的考试时间段数(可以将颜色相同的点所对应的课程安排在 同一时间)

如何定义图这个数学概念? What we have drawn in Figure 1.1 is called a graph.Formally,a graph G consists of a finite nonempty set V of objects called vertices(the singular is vertex)and a set E of 2- element subsets of V called edges.The sets V and E are the vertex set and edge set of G, G=V,E) 如果要定 E={{u,v}u,v∈V 义有向图?
如何定义图这个数学概念? G = (V ,E ) E = {{u,v}| u,v V } 如果要定 义有向图?
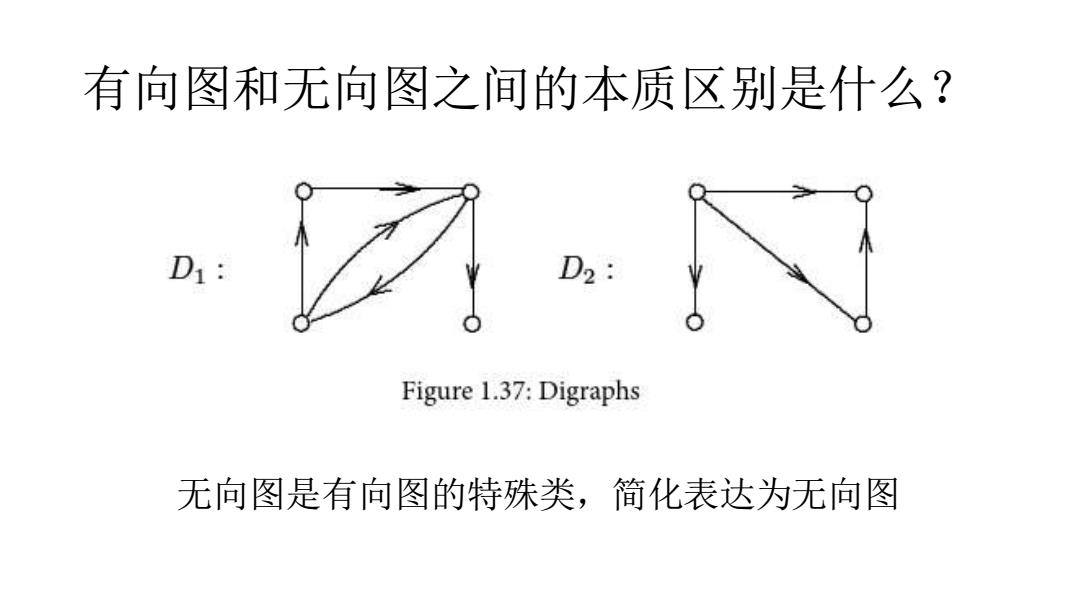
有向图和无向图之间的本质区别是什么? Figure 1.37:Digraphs 无向图是有向图的特殊类,简化表达为无向图
有向图和无向图之间的本质区别是什么? 无向图是有向图的特殊类,简化表达为无向图

如何用图进行问题建模? ·构造图节点 ·确定什么作为图节点? ·构造图中的边 ·确定什么作为图中的边? ·用图中数学语言重述待解问题 ·从自然语言到形式(数学)语言
如何用图进行问题建模? • 构造图节点 • 确定什么作为图节点? • 构造图中的边 • 确定什么作为图中的边? • 用图中数学语言重述待解问题 • 从自然语言到形式(数学)语言
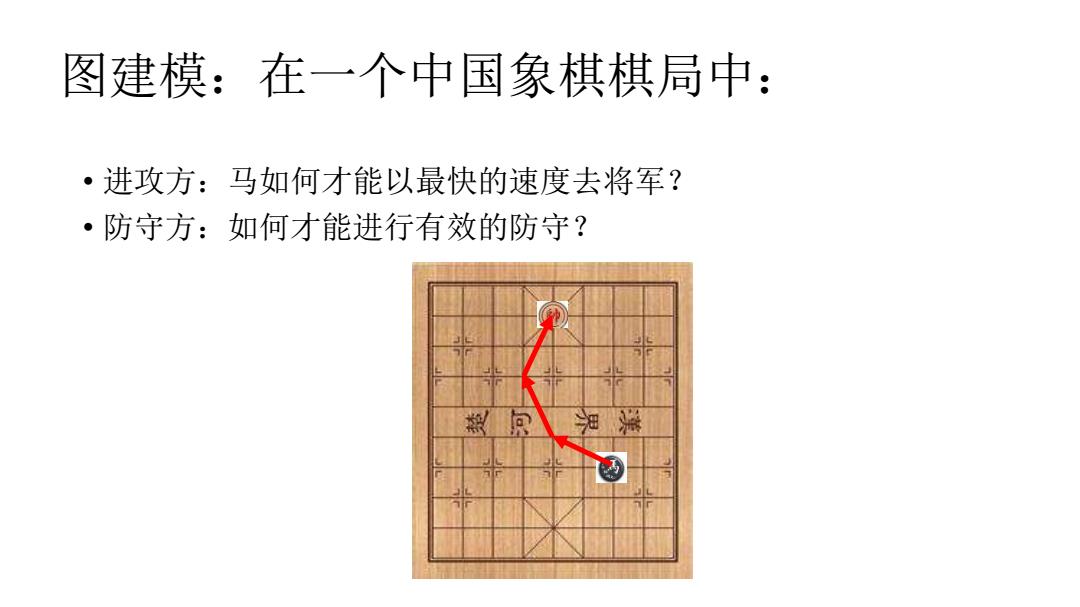
图建模:在一个中国象棋棋局中: ·进攻方:马如何才能以最快的速度去将军? ·防守方:如何才能进行有效的防守? 湘深
图建模:在一个中国象棋棋局中: • 进攻方:马如何才能以最快的速度去将军? • 防守方:如何才能进行有效的防守?

Theorem 1.6 If a graph G contains a u-v walk of length l,then G contains a u-v path of length at most I. Proof.Among all u-vwalks in G,let P=(u=40,1,,uk=V) 还有其它证 be a u-vwalk of smallest length k.Therefore,k sI.We claim that p is a u-v path. 明方法吗? Assume,to the contrary,that this is not the case.Then some vertex of Gmust be repeated in P,sayufor some iandjwithssk.If we then delete the verticesu 2.from P,we arrive at the u-vwalk 图中定理的证 (u=0,1,,1-1,4=j,uj+1,…,4以=V) 明,多用如此 whose length is less than k,which is impossible.Therefore,as claimed,P is a u-vpath 的反证法、构 of length k≤l ■ 造法
图中定理的证 明,多用如此 的反证法、构 造法 v 还有其它证 明方法吗?