
计算机问题求解一论题4-1 -群与循环群 2019年3月06日
计算机问题求解 – 论题4-1 - 群与循环群 2019年3月06日

问题1:什么是一个algebraic structures? 01234567 000000000 1 01234567 2 024 6 0 2 46 集合,及集合 3 03 6 4 7 2 5 4 04 0 0 4 0 4 上定义的若干 5 05 2 7 4 1 63 封闭的运算 6 06 4 20 6 42 707654321 Table 3.3:Multiplication table for Zs (Z8,·)
问题1:什么是一个algebraic structures? (Z8,•) 集合,及集合 上定义的若干 封闭的运算

运算及其性质 Proposition 3.1 Let Zn be the set of equivalence classes of the integers mod n and a,b,c∈Zn. 1.Addition and multiplication are commutative: 2.Addition and multiplication are associative: 3.There are both an additive and a multiplicative identity: 4.Multiplication distributes over addition: 5.For every integer a there is an additive inverse-a: 6.Let a be a nonzero integer.Then gcd(a,n)=1 if and only if there erists a multiplicative inverse b for a (mod n);that is,a nonzero integer b such that ab =1 (mod n)
运算及其性质

第二例: Figure 3.2.Symmetries of a triangle B B identity Table 3.2.Symmetries of an equilateral triangle B id P1 P21 23 rotation A B id id P1 2 1 2 3 B P1 P1 P2 id 43 41 2 P2 id 2 3 41 rotation 2 3 id P2 2 d 四 3 后 2 P1 a Q refection =(&) B 等边三角形的对称变换(函数) 在函数复合运算上构成的代 B 数系统 refection B
第二例: 等边三角形的对称变换(函数) 在函数复合运算上构成的代 数系统
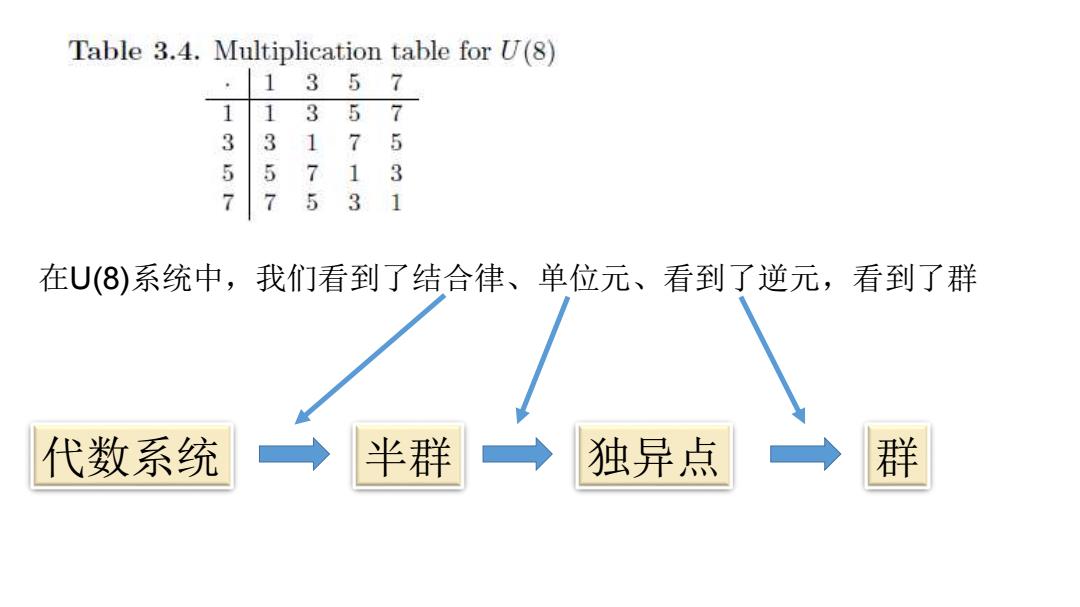
Table 3.4.Multiplication table for U(8) 3 1 5 7 1 1 3 57 3 3 175 5 5 7 1 3 7 7 5 3 1 在U(⑧)系统中,我们看到了结合律、单位元、看到了逆元,看到了群 代数系统 半群 独异点 群
在U(8)系统中,我们看到了结合律、单位元、看到了逆元,看到了群 代数系统 半群 独异点 群
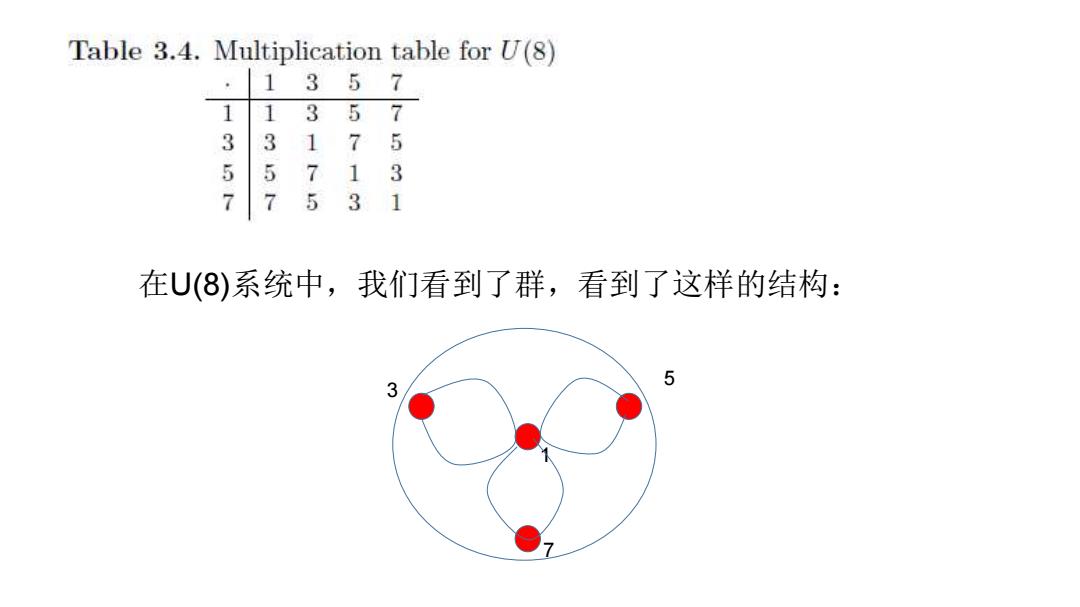
Table 3.4.Multiplication table for U(8) 3 1 5 7 1 1 3 57 3 3 1 75 5 7 13 7 7 53 1 在U(8)系统中,我们看到了群,看到了这样的结构: 5 3
在U(8)系统中,我们看到了群,看到了这样的结构: 1 3 5 7
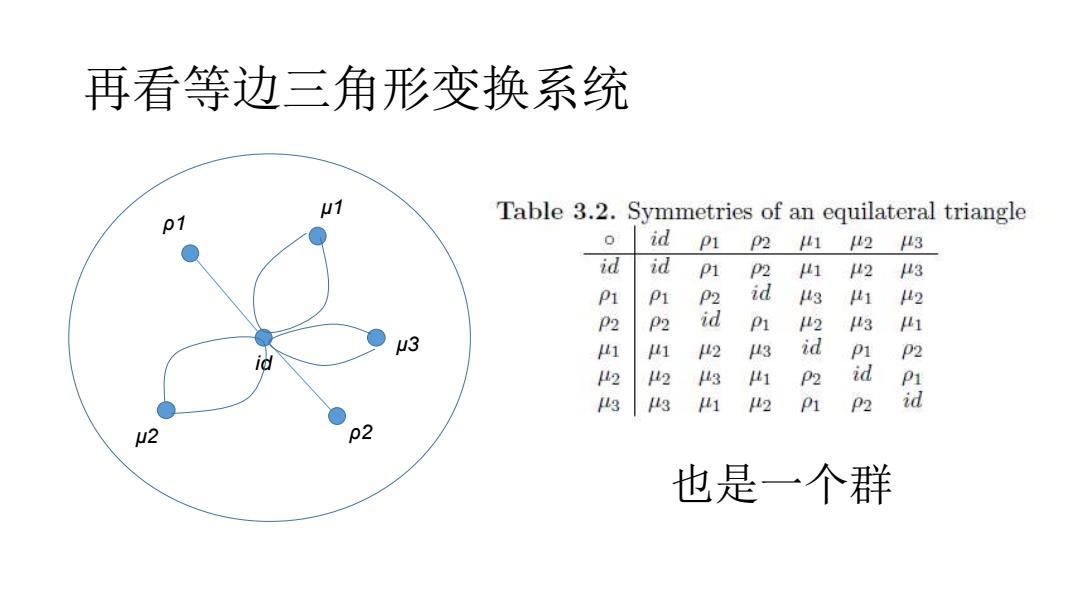
再看等边三角形变换系统 01 Table 3.2.Symmetries of an equilateral triangle id P1 P2 41 2 3 id P1 1 2 μ3 P1 id 3 1 2 P2 d P 2 3 1 U3 p 3 id P2 2 吗 a 3 a 2 也是一个群
再看等边三角形变换系统 id ρ1 ρ2 μ1 μ2 μ3 也是一个群

群-一种“公理化”定义的代数系统 The law of composition is associative.That is, 问题2:结合律 (aob)oc=ao(boc) 为什么会被放进 fora,b,c∈G. 群公理中? There exists an element e G,called the identity element,such that for any element a EG eo a=aoe a. For each element a G,there exists an inverse element in G, denoted by a-1,such that aoa-1=a-loa=e. 注意:对于the integers mod n,加法一定构成群,乘法则未必
群 – 一种“公理化”定义的代数系统 注意:对于the integers mod n,加法一定构成群,乘法则未必。 问题2:结合律 为什么会被放进 群公理中?

结合律的作用 Proposition 3.19.Let G be a group.If a,bG,then (ab)-1=b-la-1. PRooF.Let a,bEG.Therabb-a-1=aca-1aa-1=e.Similarly,b-a-ab=e.But by the previous proposition,inverses are unique;hence,(ab)-1=b-la-1
结合律的作用

一元一次方程的解 。什么情况下,ax=b有解?解是否唯一?解是什么? ·(R-0},X)具有什么性质? 群
一元一次方程的解 • 什么情况下,ax=b有解?解是否唯一?解是什么? • (R-{0},×)具有什么性质? 群