
计算机问题求解一论题4.10 启发式算法的概念 陶先平 2017年6月5日
计算机问题求解—论题4.10 启发式算法的概念 陶先平 2017年6月5日

问题1:在一个优化问题中,什么是问题 空间?什么是解空间? Let U (SI,>o,L,LI,M,cost,goal) 问题2:启发式算法本质上来讲,是一种解 空间搜索算法。你如何理解这个说法?
问题1:在一个优化问题中,什么是问题 空间?什么是解空间? 问题2:启发式算法本质上来讲,是一种解 空间搜索算法。你如何理解这个说法?

问题3:定义一个可行解的”邻居”是什么用 意? Definition 3.6.1.1.Let U (SI,So,L,LI,M,cost,goal)be an optimiza- tion problem.For every x E LI,a neighborhood on M(x)is any mapping f M(x)Pot(M(x))such that (i)a∈fx(a))for every a∈M(x, 何谓邻居?自 i)fB∈fr(a)for some a∈M(x),then a∈fr (iii)for all a,BE M(x)there exists a positive integ 由定义,因人 such that Y∈fx(a),Y+1∈fz(Y)fori=1,. 因事而不同 提示:定义的第三点,寓意深刻
问题3:定义一个可行解的”邻居”是什么用 意? 提示:定义的第三点,寓意深刻 何谓邻居?自 由定义,因人 因事而不同

可行解的邻居图 The (undirected)graph GM().f=(M(x),{fa,B)laE fz(B),a#B,a,BEM()}) is the neighborhood graph of M(x)according to the neighborhood fa. 理论上:1,邻居图连通; 2,最优解必定在图中; 3,遍历解空间的难度,决定了问题难度
可行解的邻居图 理论上:1,邻居图连通; 2,最优解必定在图中; 3,遍历解空间的难度,决定了问题难度

局部最优解 Definition 3.6.1.4.Let U =(SI,So,L,LI,M,cost,goal)be an optimiza- tion problem,and let,for every x E LI,the function fr be neighborhood on M(x).A feasible solution aE M(x)is a local optimum for the input instance x of U according to f,if cost(a)=goal{cost(3)川lB∈fx(a). 退而求其次,也是一个很好的策略
局部最优解 退而求其次,也是一个很好的策略
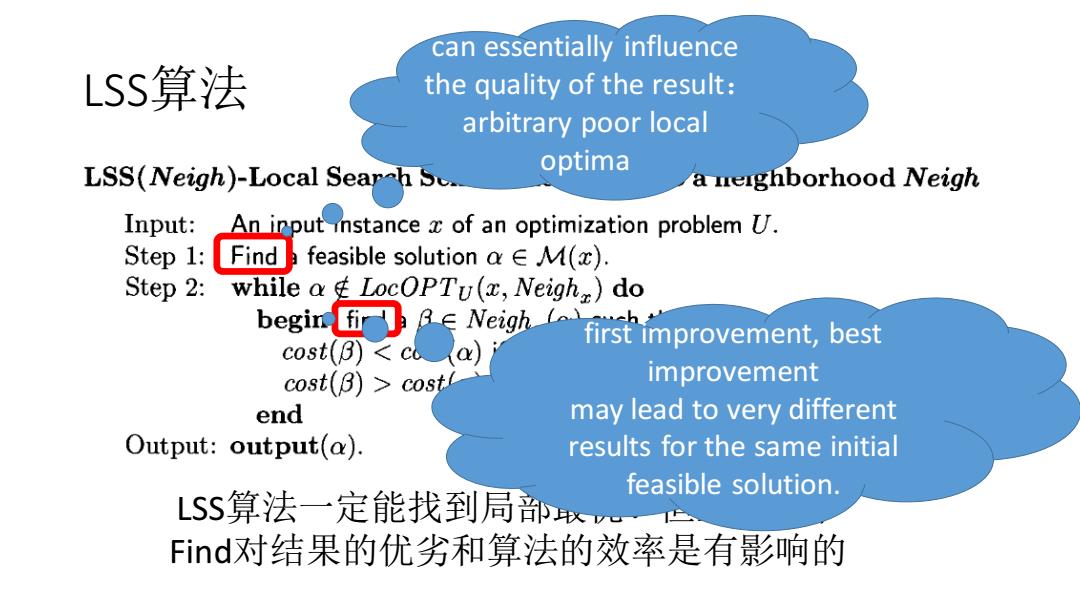
can essentially influence LSS算法 the quality of the result: arbitrary poor local LSS(Neigh)-Local Searh Sc. optima a neighborhood Neigh Input: An input instance z of an optimization problem U. Step 1:Finda feasible solution a E M(x) Step 2:while ag LocOPTu(x,Neigh)do begin fir∈Neigh cost(B)cost improvement end may lead to very different Output:output(a). results for the same initial feasible solution. LSS算法一定能找到局w Find对结果的优劣和算法的效率是有影响的
LSS算法 LSS算法一定能找到局部最优!但上述两个 Find对结果的优劣和算法的效率是有影响的 can essentially influence the quality of the result: arbitrary poor local optima first improvement, best improvement may lead to very different results for the same initial feasible solution

必须解决局部搜索方法中的 poor local optima”问题 The basic idea of simulated annealing is to add the possibility of leaving a local optimum (i.e.,to move to a weaker solution than the current one)by some kind of coin tossing (random decision)
必须解决局部搜索方法中的 “poor local optima”问题

物理学中的“退火”是什么? (1)The temperature of the heat bath is increased to a maximum value at which the solid melts.This causes all the particles to arrange themselves randomly. (2)The temperature of the heat bath is slowly decreased according to a given cooling schedule until a low-energy state of the solid (a perfect crystal structure)is achieved
物理学中的“退火”是什么?

Metropolis:算法:对退火过程的模拟 Step 1:Let s be the initial state of the solid with energy E(s)and let T be the initial temperature of the heat bath. Step 2: Generate a state g from s by applying a perturbation mechanism, which transfers s into g by a small random distortion (for instance, by a random displacement of a small particle). if E(a)<E(s)then s:=a else accept g as a new state with the probability 模拟退火算法对LSS E(Q-E( 算法的最大改进 p(s→g)=e (i.e,remain in state s with the probability 1-p(sg)). Step 3:Decrease T appropriately. if T is not too close to 0 repeat Step 2, else output(s)
Metropolis算法:对退火过程的模拟 模拟退火算法对LSS 算法的最大改进

两个方法的直观比对 Metropolis方法 LSS方法 the set of system states the set of feasible solutions ●the energy of a state the cost of a feasible solution perturbation mechanism a random choice from the neighborhood ●an optimal state an optimal feasible solution ◆temperature ·a control parameter
两个方法的直观比对 Metropolis方法 LSS方法