
计算机问题求解-论题1-3 常用证明方法及其逻辑正确性 陶先平 2019年10月22日
计算机问题求解-论题1-3 常用证明方法及其逻辑正确性 陶先平 2019年10月22日

Outlines ·反证法及其逻辑正确性 ·分情形证明法及其逻辑正确性 ·数学归纳法及其逻辑正确性 ·鸽笼原理证明法及其逻辑正确性
Outlines • 反证法及其逻辑正确性 • 分情形证明法及其逻辑正确性 • 数学归纳法及其逻辑正确性 • 鸽笼原理证明法及其逻辑正确性

V2 is not rational (Pythagoreans)? Proof. Suppose,to the contrary,that v2 is rational.Then there exist inte- gers p and q(with q nonzero)such that v2=p/q.We may assume that p and q have no common factor,for if they did,we would sim- plify and begin again.Now,we have that v2q p.Squaring both sides,we obtain 2g2 =p2.Thus p2 is e s even, we know from Problem 3.1 that p m 你有没有怀疑过 2m for some integer m.This means t 这个"therefore” see that g2 =2m2.But this means that a 的正确性? m Prob- lem 3.1 that g is even.So p and 2,which is completely absurd,since we assumed ne o common factor. Therefore our assumption that v2 is rational must be wrong and we have completed the proof of the theorem. ■
2 is not rational (Pythagoreans)? 你有没有怀疑过 这个”therefore” 的正确性?

There are infinitely many prime numbers. Proof. We set a contrary of To prove this statement suppose,to the contrary,that there are our theorem and use finitely many primes.Then we may write these finitely many this assumption to primes in ascending order as start 2,3,5,,N, where N is the largest prime.Now consider the number M defined by Then we get a M=(2·3.5·…·N+1 contradiction through If M is prime,then M is a prime that is larger than the largest prime a valid argument N.Therefore,we must conclude that M is not prime,and so it is divisible by some prime number,P.However,P must appear inthe list of primes 2,3,5, which we gave earlier.Bu when we divide M by P,we obtain a Then we get the remainder of1 Therefore,P cannot be a factor of M and we have theorem quickly contradicted our assumption tha there are finitely many primes. Thus,tere cxist infinitely many primes. ■
There are infinitely many prime numbers. We set a contrary of our theorem and use this assumption to start Then we get a contradiction through a valid argument Then we get the theorem quickly
反证法的逻辑正确性必定来自于逻辑! ·令:A表示V2不是有理数;B(p,q)表示m和n互质 ·假定A成立 ·推理: /注意以下推理 中p和g的辖域 ·A ·3p3q V=B(p.Q) (A,若干数学定理)→F 0 其实,这两步 T→(A∧若干数学定理) ·p2=2q2 之间的逻辑还 ·p是偶数, (AA若干数学定理)=F 令p=2m 挺复杂,更为 ·q是偶数 A =F 本质! ·Bp,q)NB(p,qg A=T ·False ·A=T
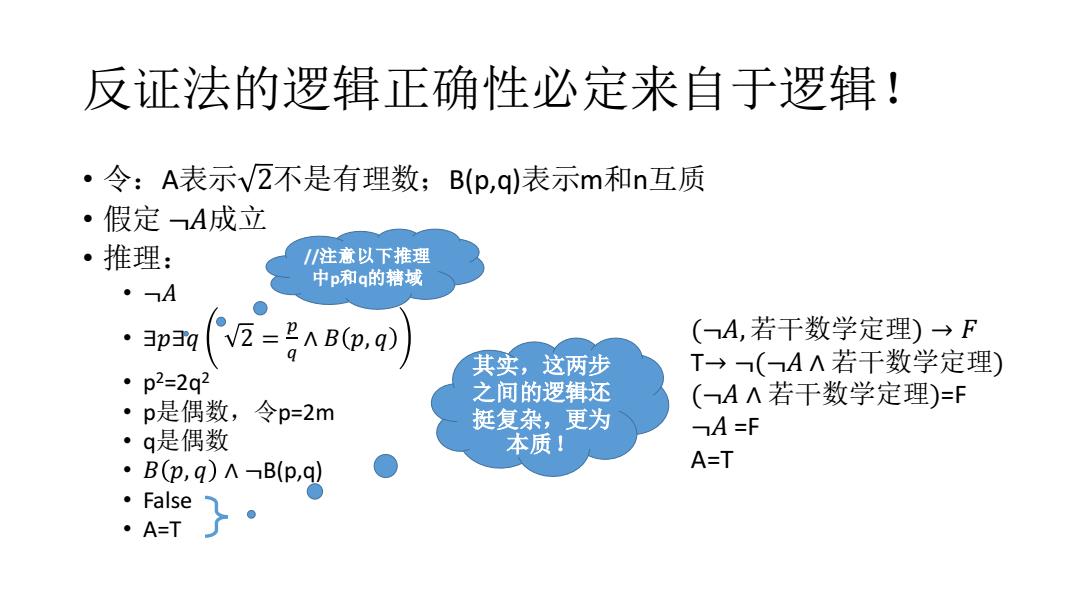
反证法的逻辑正确性必定来自于逻辑! • 令:A表示 2不是有理数;B(p,q)表示m和n互质 • 假定 ¬𝐴成立 • 推理: • ¬𝐴 • ∃𝑝∃𝑞 2 = 𝑝 𝑞 ∧ 𝐵 𝑝, 𝑞 • p 2=2q2 • p是偶数,令p=2m • q是偶数 • 𝐵 𝑝, 𝑞 ∧ ¬B(p,q) • False • A=T (¬𝐴, 若干数学定理) → 𝐹 T→ ¬(¬𝐴 ∧ 若干数学定理) (¬𝐴 ∧ 若干数学定理)=F ¬𝐴 =F A=T //注意以下推理 中p和q的辖域 其实,这两步 之间的逻辑还 挺复杂,更为 本质!

反证法的逻辑正确性必定来自于逻辑! ·定理证明: ·前提:一组命题公式A1,A2,…,Ak ·结论:一个命题公式B ·如果是这样: 问题1:在这个一般性的 · 前提:一组命题公式7B,A1,A2,…,Ak 定理证明过程中,你现在 ·结论:F 能说清楚反证法的基本方 ·即:7B,A1,A2,,A=>f 法和它的逻辑正确性吗? ·7BΛA1∧A2Λ.Ak=F ·A1,42,,A4为真 ·B=F ·B=T
反证法的逻辑正确性必定来自于逻辑! • 定理证明: • 前提:一组命题公式A1 , A2 , …, Ak • 结论:一个命题公式B • 如果是这样: • 前提:一组命题公式¬ B,A1 , A2 , …, Ak • 结论:F • 即:¬ B,A1 , A2 , …, Ak=>F • ¬ B ∧ A1 ∧ A2 ∧ … ∧Ak=F • A1 , A2 , …, Ak为真 • ¬ B=F • B=T 问题1:在这个一般性的 定理证明过程中,你现在 能说清楚反证法的基本方 法和它的逻辑正确性吗?

问题2 ·反证法有时比直接证明法更好用。你能说说为什么吗? ·如果需要你证明如下定理,你有什么想法? ·前提:A1,A2,.,Am ·结论:B1或者B2或者.或者Bn
问题2 • 反证法有时比直接证明法更好用。你能说说为什么吗? • 如果需要你证明如下定理,你有什么想法? • 前提:A1,A2,…,Am • 结论:B1或者B2或者…或者Bn

Theorem 5.3. Let x and y be real numbers.Then lxyl lxllyl. Proof. 问题3:这种证明方法 First,suppose that x 0 and y 0.Then xy 0 and we have 为什么被称为分情形证 Ixyl =xy,xl=x,and lyl =y.Therefore, 明法? Ixyl =xy Ixllyl, and we have established the result in this case. Second,suppose that x0.Then 问题4:这种证明方法 xy 0 and we have lxyl =-(xy),lxl =-x,and lyl y.Therefore, 最“令人担心”的是什 x=-(0=(-x)y=xl 么? We have now established the result for all four possible cases and we may conclude that lxyl =Ixllyl for all real numbers x and y
问题3:这种证明方法 为什么被称为分情形证 明法? 问题4:这种证明方法 最“令人担心”的是什 么? 问题5:有的时候,我 们在证明时会用到“不 失一般性”这个词,你 理解这是什么意思吗?

问题6:你能用学过的逻辑知识说明分情 形证明法的正确性吗? ·证明p→q,如果恰有p=p1Vp2V…Vpn则有: ·(p→q)=(p1→q)A(p2→q)∧.A(pn→q) ·因此: P=p1Vp2vvpn成为关键所在,成为这种证明方法的“令人担心”的地
问题6:你能用学过的逻辑知识说明分情 形证明法的正确性吗? • 证明p→q,如果恰有pp1 p2 … pn, 则有: • (p→q) (p1 →q) (p2 →q) … (pn →q) • 因此: • pp1 p2 … pn成为关键所在,成为这种证明方法的“令人担心”的地 方

存在性证明 ·证明具有某种性质的对象的存在性 ·3xp(x) ·基本方法: ·构造法:找到一个a,p(a)=T ·非构造法:归谬证明Vx一p(x)=F ·讨论题: ·Chomp游戏,你该如何幸存?
存在性证明 • 证明具有某种性质的对象的存在性 • xp(x) • 基本方法: • 构造法:找到一个a,p(a)=T • 非构造法:归谬证明xp(x) = F • 讨论题: • Chomp游戏,你该如何幸存?