
计算机问题求解-论题1-13 -布尔代数 2020年2月20日
计算机问题求解--论题1-13 --布尔代数 2020年2月20日

问题1:这个是布尔代数的定义,你有没有一种熟悉的感 觉?它和另一个定义有什么异同之处?你能想到什么? Let B be a nonempty set with two binary operations and *a unary operation',and two distinct elements 0 and 1.Then B is called a Boolean algebra if the following axioms hold where a.b.c are any elements in B: [B:] Commutative laws: (la)a+b=b+a (1b) a*b=b米a [B2] Distributive laws: (2a)a+(b*c)=(a+b)*(a+c) (2b) a*(b+c)=(a*b)+(a*c) [Ba] Identity laws: (3a)a+0=a (3b) a*1=a B Complement laws: (4a)a+a'=1 (4b)a*a=0 Axioms Defining a Lattice Let L be a nonempty set closed under two binary operations called meer and join,denoted respectively by A and v.Then L is called lattice if the following axioms hold where a,b.c are elements in L: [LI]Commutative law: (1a)a八b=bAa (1b)avb=bva [L2]Associative law: (2a)(aAb)Ac=a(bA e) (2b)(av b)vc=av(bv e) [L3]Absorption law: (3a)a (avb)=a (3b)av(aAb)=a We will sometimes denote the lattice by (L.A,V)when we want to show which operations are involved
问题1:这个是布尔代数的定义,你有没有一种熟悉的感 觉?它和另一个定义有什么异同之处?你能想到什么?

“这个”代数和格 Theorem 15.2:Let a,b,c be any elements in a Boolean algebra B. (①) Idempotent laws: (5a)a+a=a (5b) a米a=a (ii) Boundedness laws: 6a)a+1=1 (6b) a*0=0 (iii) Absorption laws: 0丰0米写a (7b) a*(a+b)=a (iv) Associative laws: (8a)(a++c三a+(b+c) (8b)(a*b)*c=a*(b*c) 问题2:显然,这个代数一定是个格!那么:多出来的那些特性 (有补、分配、恒等),有什么用呢?
“这个”代数和格 问题2:显然,这个代数一定是个格!那么:多出来的那些特性 (有补、分配、恒等),有什么用呢?

我们可以很容易的验证B3是布尔代数 (b)Let B=B x B x...x B(n factors)where the operations of+,*and'are defined componentwise using Fig.15-1.For notational convenience,we write the elements of B"as n-bit sequences without commas,e.g.. x =110011 and y 111000 belong to B".Hence x+y=111011,x*y=110000,x′=001100 111 Then B is a Boolean algebra.Here 0=000...0 is the zero element,and 1 =111...I is the unit element. 110 101 011 问题3:从这个B3中,我们能否设计一个“类似”的格? 元素有哪些?偏序关系是什么? 010 100 001 meet和join分别是什么? Bn有几个元素? 000 B3
我们可以很容易的验证B3是布尔代数 001 111 110 101 011 010 100 000 B3 问题3:从这个B3中,我们能否设计一个“类似”的格? 元素有哪些?偏序关系是什么? meet和join分别是什么? Bn有几个元素?

其实,布尔代数是一类特别的格: ·1,我们可以从布尔代数和偏序集两个角度共同定义一个“系统” ·2,布尔代数和有界有补分配格是“等价”的 从同构的角度上讲,布尔代数、有界有补分配格、集合幂集运算格,同构! 请问:三个同构的系统,是如何同构的?
其实,布尔代数是一类特别的格: • 1,我们可以从布尔代数和偏序集两个角度共同定义一个“系统” • 2,布尔代数和有界有补分配格是“等价”的 从同构的角度上讲,布尔代数、有界有补分配格、集合幂集运算格,同构! 请问:三个同构的系统,是如何同构的?

问题4: ·有限有补分配格一定有2n个元素 因为B1,B2,B3,..,Bn有2n个元素? 其实,我们还可以这样来观察: 1,这样的格中,原子个数是n个 2,除0外,所有元素都可以表示为一个或者多个原子的 join,所有由一个或者多个原子的join的结果都是格中元素。 3,这样的元素有2n.1个
问题4: • 有限有补分配格一定有2 n个元素 因为B1,B2,B3,…,Bn有2 n个元素? 其实,我们还可以这样来观察: 1,这样的格中,原子个数是n个 2,,除0外,所有元素都可以表示为一个或者多个原子的 join,所有由一个或者多个原子的join的结果都是格中元素。 3,这样的元素有2 n -1个
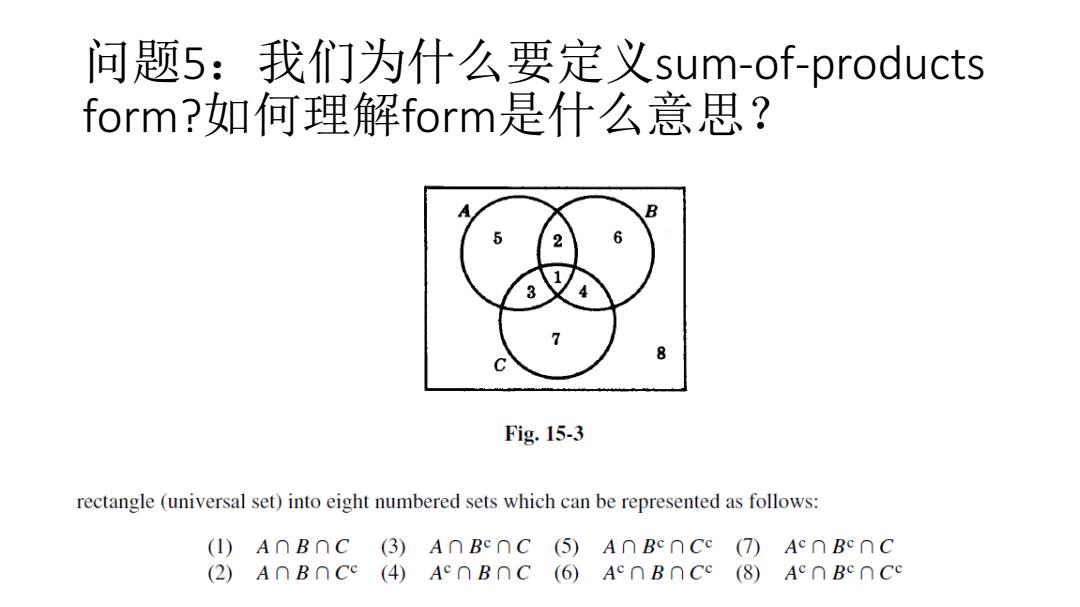
问题5:我们为什么要定义sum-of-products form?如何理解form是什么意思? Fig.15-3 rectangle(universal set)into eight numbered sets which can be represented as follows: (I)A∩B∩C(3)A∩Bc∩C(5)A∩Be∩Cc(T)Ac∩Bc∩C (2)A∩BnCe(4)Ac∩B∩C(6)Ac∩BnCe(8)Ac∩BenCc
问题5:我们为什么要定义sum-of-products form?如何理解form是什么意思?

问题6:任意的布尔代数运算表达式,是否都 可以表达为某个"sum-of-products form"? E=(x+y)+(xyz+x'y)'and E2=((xy'z+y)'+x'z)' Theorem 15.8:Every nonzero Boolean expression EE(x1,x2,...,x)is equivalent to a complete sum-of-products expression and such a representation is unique. 这个定理为我们证明两个逻辑(布尔)表达式的等价带来了极大的便利!
问题6:任意的布尔代数运算表达式,是否都 可以表达为某个”sum-of-products form”? 这个定理为我们证明两个逻辑(布尔)表达式的等价带来了极大的便利!

复习几个概念: Literal?Fundamental product?Contained in? E=xz'+y'z+xyz'and E2=xz+x'yz'+xy'z Contained in? Observe that if P is contained in P2.say P2=P*then,by the absorption law. P1+P2=P1+P1*Q=P Thus,for instance,x+x'y=x
复习几个概念: Literal?Fundamental product?Contained in? Contained in?

布尔表达式的积和表达: ·1,如果该布尔表达式是一个基本积项: ·2,如果该布尔表达式是两个或者多个基本积项的和 ·任意积项都不包含于另外的积项中 E=xz+y'z+xyz'and E2=xz +x'yz'+xy'z X
布尔表达式的积和表达: • 1,如果该布尔表达式是一个基本积项; • 2,如果该布尔表达式是两个或者多个基本积项的和 • 任意积项都不包含于另外的积项中 X √