
计算机问题求解一论题2-6 算法方法 2022年3月30日
计算机问题求解 – 论题2-6 - 算法方法 2022年3月30日

搜索“解空间”-一个例子 ■一位父亲请一位数学家猜他3个孩子的年龄,他提示说: 口3人年龄的乘积是36。 0 这时他们恰好经过一幢房子,父亲又提示说:他们年龄之和等于这房 子窗户的个数13。 ■父亲见数学家仍然犹豫,又补充说: 口老大很小的时候家中没有其他孩子跟他一起玩。 ·你能说出3个孩子的年龄吗?
搜索“解空间” – 一个例子 ◼ 一位父亲请一位数学家猜他3个孩子的年龄,他提示说: ❑ 3人年龄的乘积是36。 ❑ 这时他们恰好经过一幢房子,父亲又提示说:他们年龄之和等于这房 子窗户的个数13。 ◼ 父亲见数学家仍然犹豫,又补充说: ❑ 老大很小的时候家中没有其他孩子跟他一起玩。 ◼ 你能说出3个孩子的年龄吗?
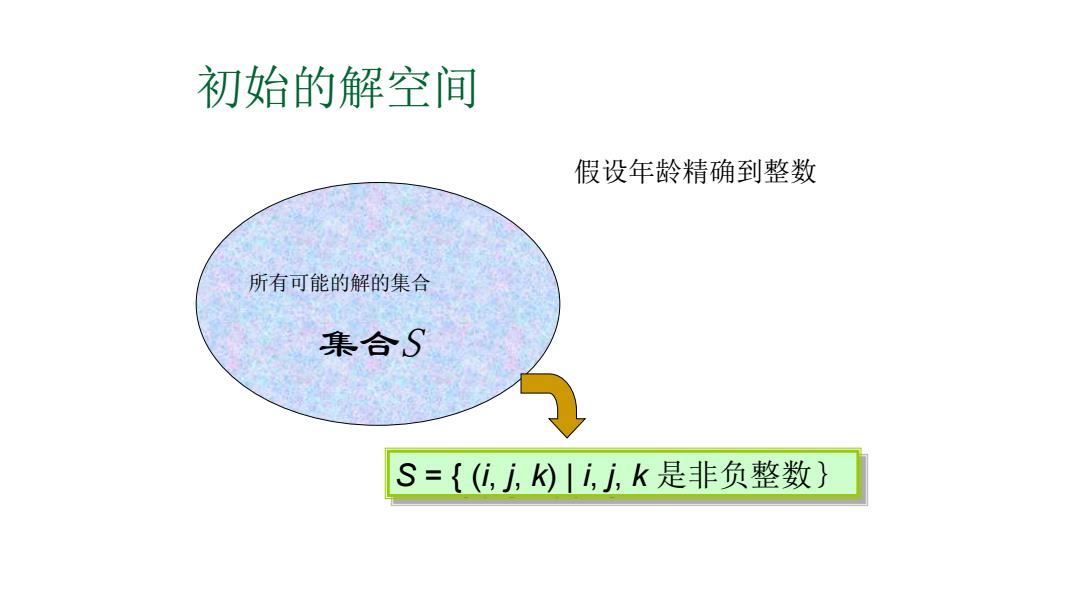
初始的解空间 假设年龄精确到整数 所有可能的解的集合 集合S S={(0,方,k|i,,k是非负整数}
初始的解空间 假设年龄精确到整数 集合S 所有可能的解的集合 S = { (i, j, k) | i, j, k 是非负整数}
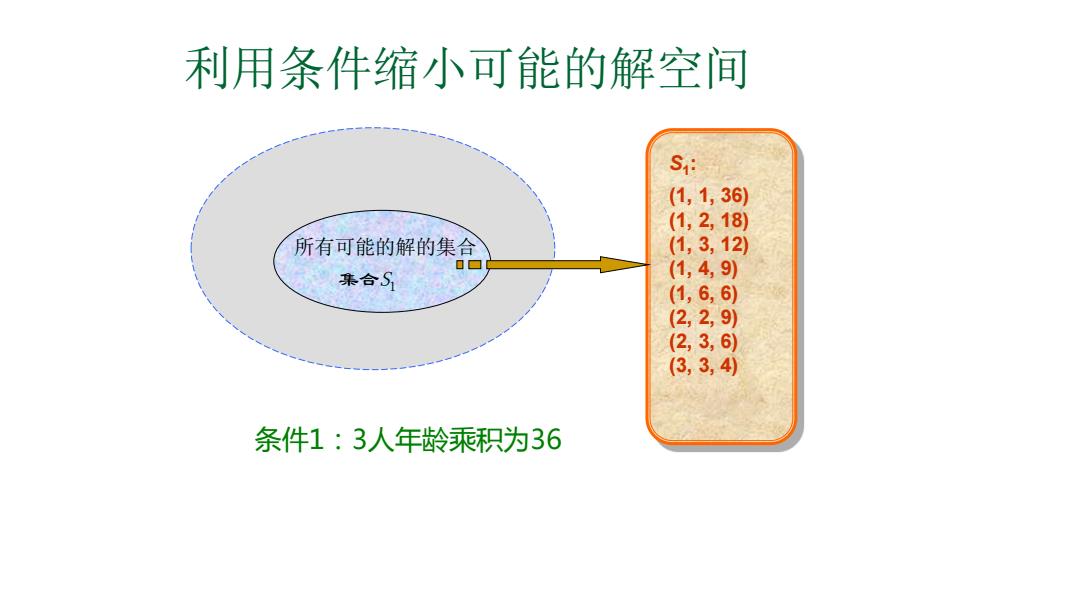
利用条件缩小可能的解空间 S (1,1,36) (1,2,18) 所有可能的解的集合 (1,3,12) 集合S (1,4,9) (1,6,6) 2,2,9) (2,3,6) (3,3,4) 条件1:3人年龄乘积为36
利用条件缩小可能的解空间 集合S1 所有可能的解的集合 S1 : (1, 1, 36) (1, 2, 18) (1, 3, 12) (1, 4, 9) (1, 6, 6) (2, 2, 9) (2, 3, 6) (3, 3, 4) 条件1:3人年龄乘积为36
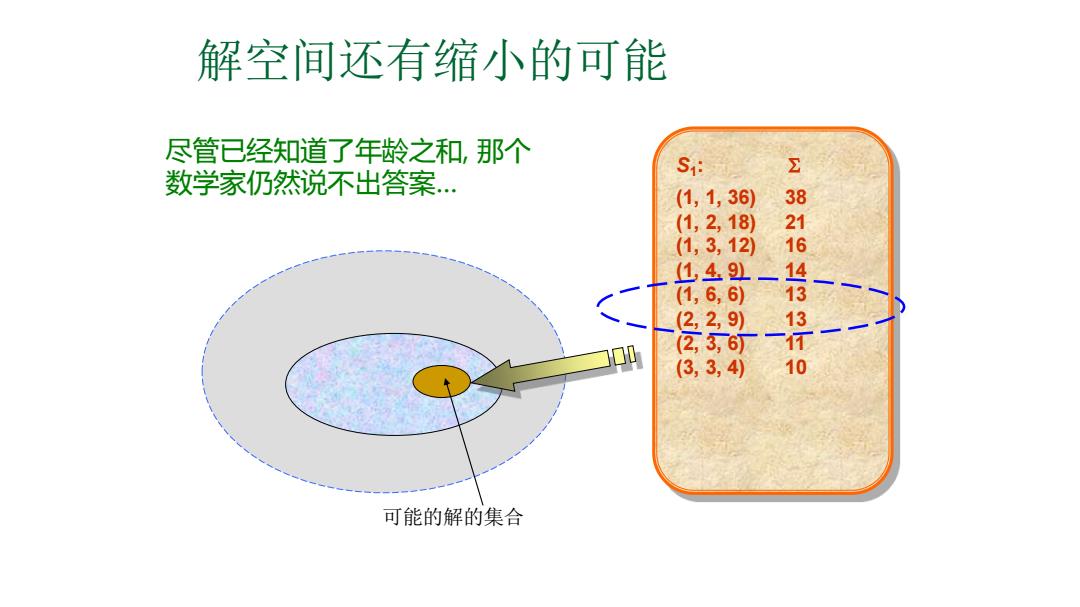
解空间还有缩小的可能 尽管已经知道了年龄之和,那个 数学家仍然说不出答案 S (1,1,36) (1,2,18) (1,3,12) 38116 L41 ,6,) 22,9) 00 Z,3 41313T10 (3,3,4) 可能的解的集合
解空间还有缩小的可能 尽管已经知道了年龄之和, 那个 数学家仍然说不出答案… S1 : (1, 1, 36) 38 (1, 2, 18) 21 (1, 3, 12) 16 (1, 4, 9) 14 (1, 6, 6) 13 (2, 2, 9) 13 (2, 3, 6) 11 (3, 3, 4) 10 可能的解的集合

再进一步就是解! ■当前可能的解的集合: {(1,6,6),(2,2,9)} ■但是:老大没有同年龄的兄弟姐妹 。因此三个孩子的年龄分别是: 9岁、2岁和2岁
再进一步就是解! ◼ 当前可能的解的集合: { (1,6,6), (2,2,9) } ◼ 但是:老大没有同年龄的兄弟姐妹. ◼ 因此三个孩子的年龄分别是: 9岁、2岁和2岁

问题求解的基本“方法” ■确定合理的解空间,并表示为某种“结构”。 ■利用已知的限制条件(知识)尽可能快的压缩可能的解空间。 口当解空间已经足够小,我们就可以“直接”解题。 如果很难确定解空间的范围,或者很难有效地缩小解空间,这 个题目就“很难
问题求解的基本“方法” ◼ 确定合理的解空间,并表示为某种“结构”。 ◼ 利用已知的限制条件(知识)尽可能快的压缩可能的解空间。 ❑ 当解空间已经足够小,我们就可以“直接”解题。 ◼ 如果很难确定解空间的范围,或者很难有效地缩小解空间,这 个题目就“很难

问题1: 你能解释一下解Maximal Polygon Distance问题的过程中 是如何建立并缩小解空间的吗?
问题1.1: 解空间是什么? 解的结构是什么? 问题1.2: 解空间的第一次压 缩是如何进行的?
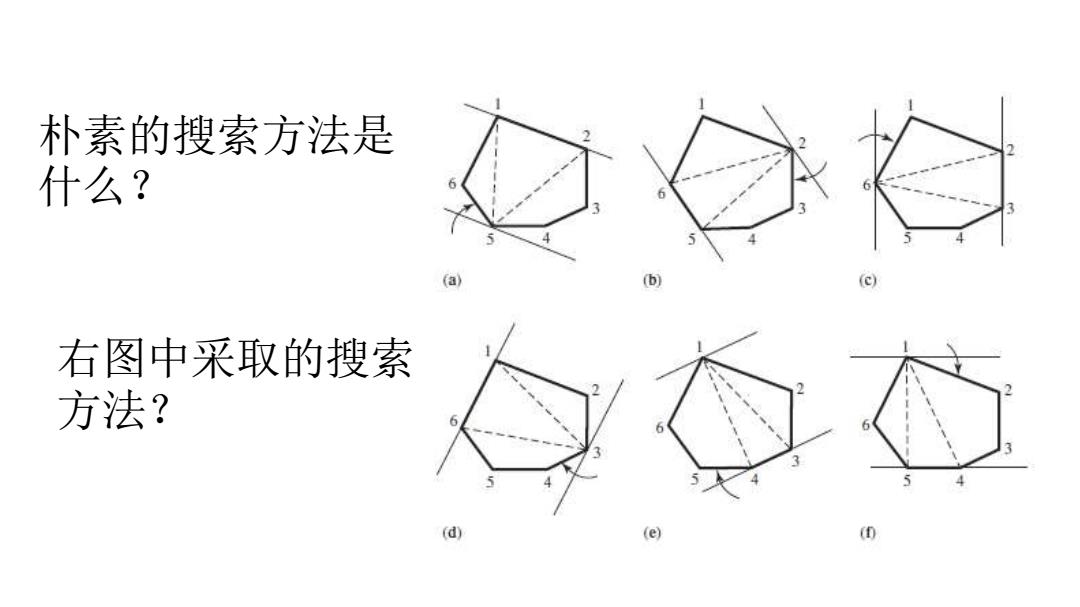
朴素的搜索方法是 什么? 右图中采取的搜索 方法? d e (0
朴素的搜索方法是 什么? 右图中采取的搜索 方法?