
计算机问题求解一论题3-7 树 2020年10月20日
计算机问题求解 – 论题3-7 - 树 2020年10月20日

Theorem 4.1 An edge e of a graph G is a bridge if and only if e lies on no cycle of G. tree:无环连通图 推论:Every edge in a tree is a bridge 问题1g 从应用的角度看。上述推论有何指导意义?
Theorem 4.1 An edge e of a graph G is a bridge if and only if e lies on no cycle of G. 推论:Every edge in a tree is a bridge tree:无环连通图
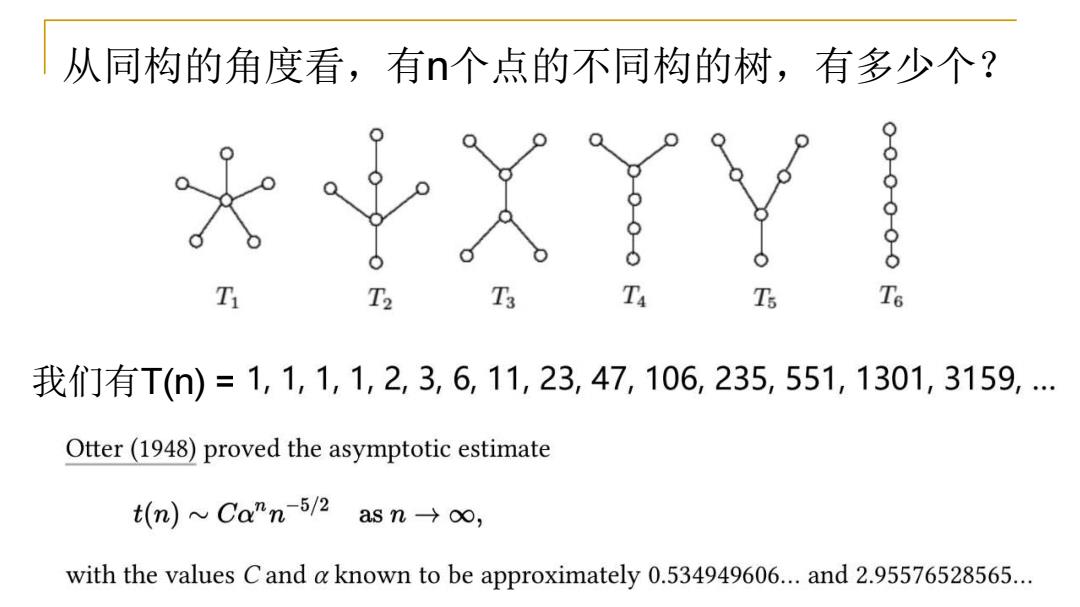
从同构的角度看,有个点的不同构的树,有多少个? T2 T, 我们有T()=1,1,1,1,2,3,6,11,23,47,106,235,551,1301,3159,… Otter(1948)proved the asymptotic estimate t(n)~Ca"n5/2asn→o, with the values C and a known to be approximately 0.534949606...and 2.95576528565
从同构的角度看,有n个点的不同构的树,有多少个? 我们有T(n) =

树、根树和有向树有什么差别? 备注:如果我们只谈树,没有父子兄弟之概念
树、根树和有向树有什么差别? 备注:如果我们只谈树,没有父子兄弟之概念

For an n-vertex graph G(with n>1),the following are equiv- alent(and characterize the trees with n vertices). A)G is connected and has no cycles. B)G is connected and has n-1 edges. C)G has n-1 edges and no cycles. D)For u,vV(G),G has exactly one u,v-path. 问题2: 如何证明一系列命题等价? 问题38 不能有回路对最小顶点度数有什么影响?

树的性质的“极限性” a)Every edge of a tree is a cut-edge. b)Adding one edge to a tree forms exactly one cycle. c)Every connected graph contains a spanning tree. 间题4: 什么样的图生成树是唯一的,为什么?
树的性质的“极限性

关于树的另外一个性质 Theorem 4.9 Let T be a tree of order k.If G is a graph withδ(可≥k-1,then T is isomorphic to some subgraph of G
关于树的另外一个性质 Theorem 4.9 Let T be a tree of order k. If G is a graph with δ(G) ≥ k − 1, then T is isomorphic to some subgraph of G

如何构造一个连通图的生成树?
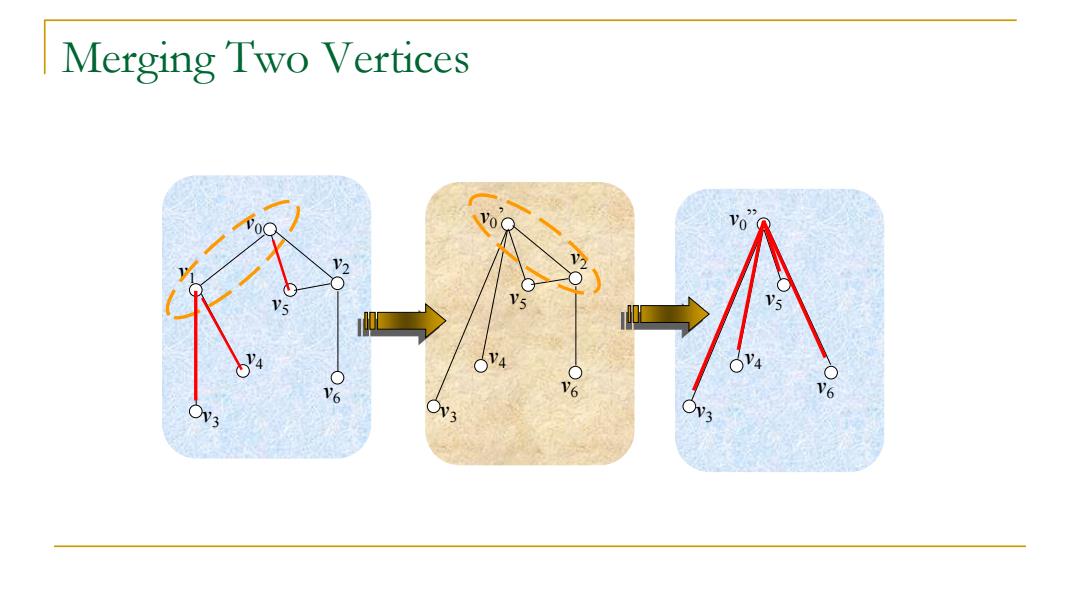
Merging Two Vertices V6
Merging Two Vertices v0 v6 v2 v5 v4 v1 v3 v6 v2 v5 v4 v3 v0 ’ v6 v5 v4 v3 v0
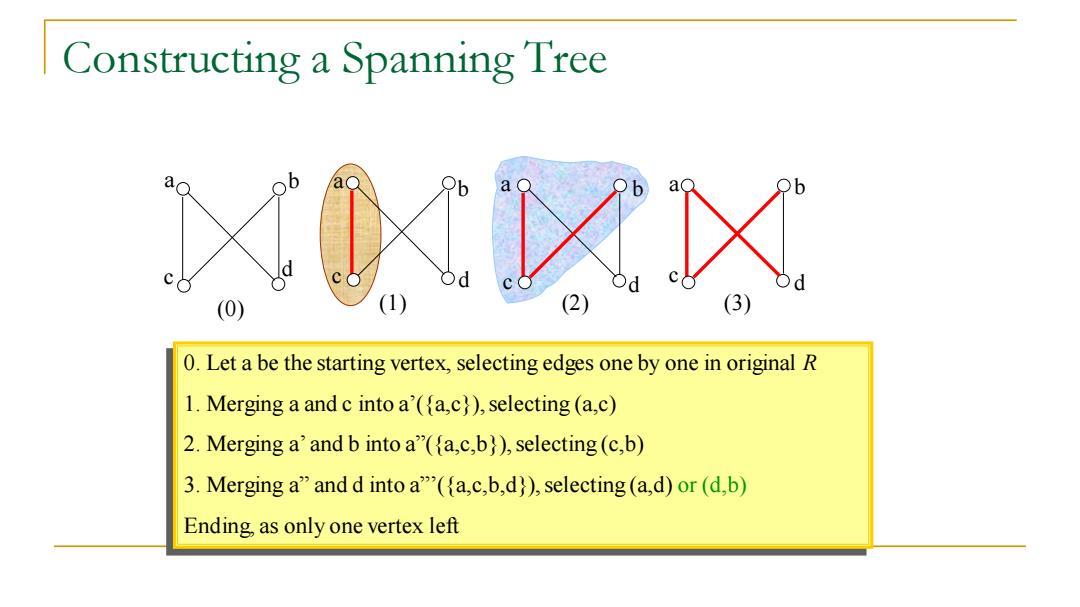
Constructing a Spanning Tree a a 1 0.Let a be the starting vertex,selecting edges one by one in original R 1.Merging a and c into a'(fa,c)),selecting (a,c) 2.Merging a'and b into a"(fa,c,b)),selecting (c,b) 3.Merging a"and d into a"(a,c,b,d)),selecting (a,d)or(d,b) Ending,as only one vertex left
Constructing a Spanning Tree a b c d a b a b a b c c d c d d 0. Let a be the starting vertex, selecting edges one by one in original R 1. Merging a and c into a’({a,c}), selecting (a,c) 2. Merging a’ and b into a”({a,c,b}), selecting (c,b) 3. Merging a” and d into a”’({a,c,b,d}), selecting (a,d) or (d,b) Ending, as only one vertex left (0) (1) (2) (3)