
计算机问题求解一论题3-14 矩阵计算 2020年12月22日
计算机问题求解 – 论题3-14 - 矩阵计算 2020年12月22日

矩阵的逆与线性方程组的解 ax1+a12x2+…+arxa=b】 a2ix1+a2x2+…+a2ra=b anix1十a2x2十…+AnnXn=bm 一一一一一一一 all a12 din b 021 a22 a2n X2 ani an2 ann Xn or,equivalently,letting A =(a),x=(xi),and b =(b:).as Ax =b. If A is nonsingular,it possesses an inverse A,and =Ab
矩阵的逆与线性方程组的解

问题1: 为什么通常不直接用求 逆矩阵的办法来解线性 方程组?

逆矩阵存在的条件 A square matrix has full rank if and only if it is nonsingular A matrix A has full column rank if and only if it does not have a null vector. A square matrix A is singular if and only if it has a null vector. An n x n matrix A is singular if and only if det(A)=0. 这是什么意思?
逆矩阵存在的条件 这是什么意思?

问题2: 如何计算非奇异矩阵的逆? 1:矩阵A的逆=A的伴随矩阵/行列式A的值 2:矩阵A的逆:对(AE)进行行初等变换得到(EA1)
1:矩阵A的逆=A的伴随矩阵/行列式A的值 2:矩阵A的逆:对(A|E)进行行初等变换得到(E|A-1 )

2 21 例:求3阶方阵A= 3 15 的逆矩阵。 323 解:1A|=1,M1=-7,M2=6,Ms=3, M21=4,M2=3,Mg=-2, 问题3.1:求 M31=9,M2=7,M3=-4, N阶方阵的逆, 时间复杂度多 则 A=A=A- 少? An A2 An A Az Mu-Ma M3 (_7 -4 -Mp Mn -M32 6 3 -7 M3 -M3 Ms 32 4
问题3.1:求 N阶方阵的逆, 时间复杂度多 少?
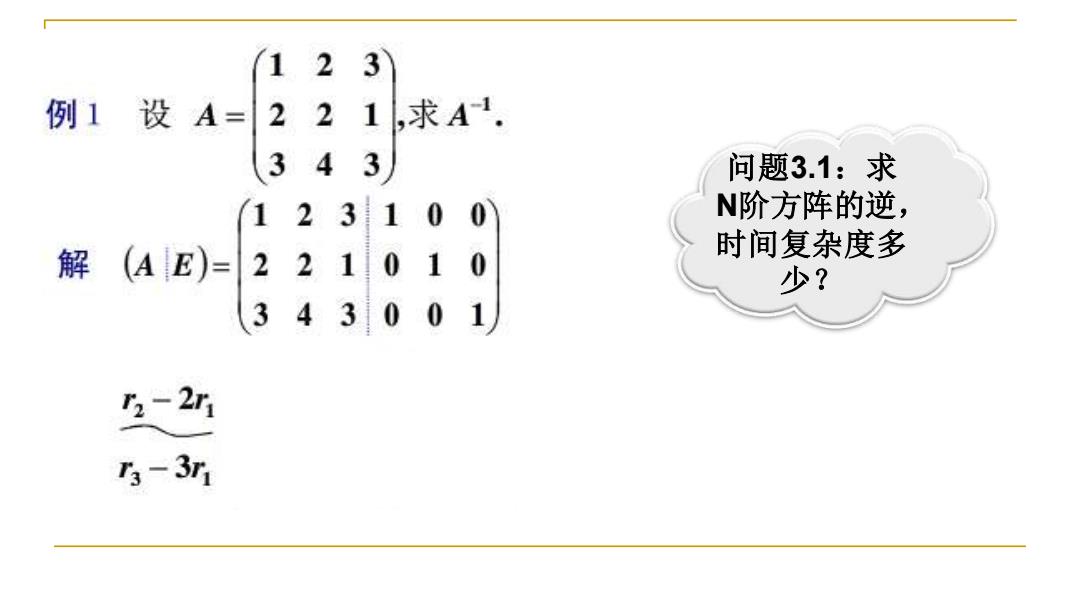
12 3 例1设A= 22 1,求A1. 343 问题3.1:求 123100 N阶方阵的逆, 解 (AE)= 221010 时间复杂度多 少? 343001 2-2 53-3r1
…… 问题3.1:求 N阶方阵的逆, 时间复杂度多 少?
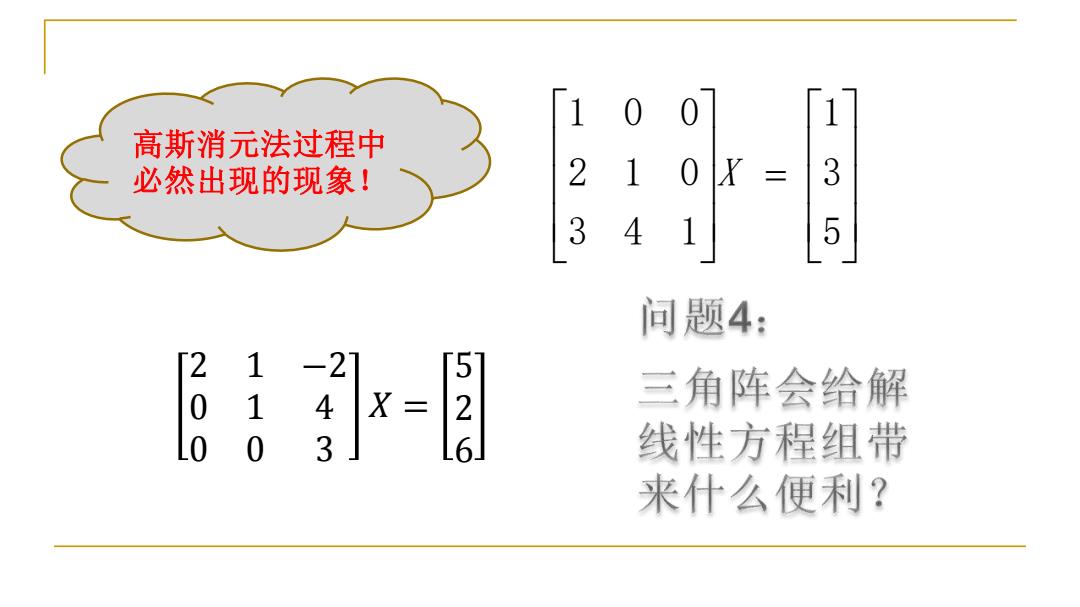
1 0 1 高斯消元法过程中 必然出现的现象! 2 1 0 Y= 3 3 4 1 5 问题4: 200 1 2 X= 526 三角阵会给解 10 线性方程组带 来什么便利?
= 5 3 1 3 4 1 2 1 0 1 0 0 X 2 1 −2 0 1 4 0 0 3 𝑋 = 5 2 6 高斯消元法过程中 必然出现的现象!

问题5: 三角阵确实会极大简化方程求解,但是 多数情况下,我们不会遇到三角阵。 Ax =b 怎么办? 任意的非奇异矩阵均能保证可以分解为两个 上、下三角矩阵的乘积
怎么办? 任意的非奇异矩阵均能保证可以分解为两个 上、下三角矩阵的乘积

假如: aAx=b==》LUX=b ■1,求方程Ly=b的解 ■2,求方程Ux=y的解 轻松愉快
假如: ◼ Ax=b ==》LUx=b ◼ 1,求方程Ly=b的解 ◼ 2,求方程Ux=y的解 轻松愉快