
网络流算法 马骏(majun@nju.edu.cn)
网络流算法 马骏(majun@nju.edu.cn)
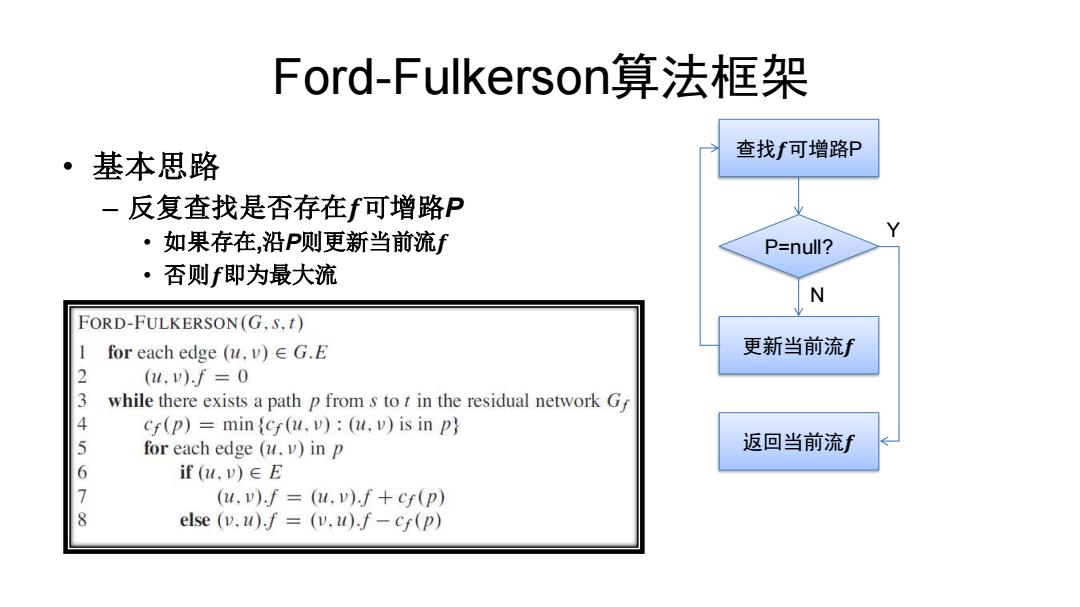
Ford-Fulkerson算法框架 ·基本思路 查找f可增路P -反复查找是否存在f可增路P ·如果存在,沿P则更新当前流f P=null? ·否则f即为最大流 N FORD-FULKERSON(G.S.t) for each edge (u.v)EG.E 更新当前流f 2 (4,v)f=0 while there exists a path p from s to t in the residual network Gf 4 cf(p)=mincf(u.v):(u.v)is in p 5 for each edge (u.v)in p 返回当前流f if(u,v)∈E 7 (u.v).f=(u.v).f+cf(p) 8 else (v.u).f =(v.u).f-cf(p)
Ford-Fulkerson算法框架 • 基本思路 – 反复查找是否存在𝒇可增路P • 如果存在,沿P则更新当前流𝒇 • 否则𝒇即为最大流 查找𝒇可增路P P=null? 更新当前流𝒇 返回当前流𝒇 N Y
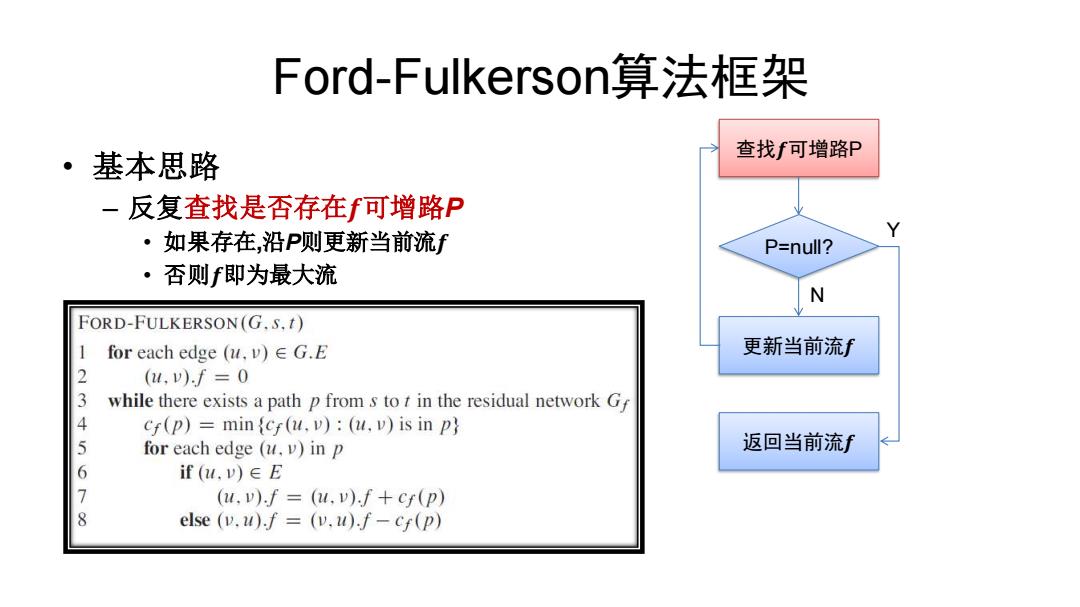
Ford-Fulkerson算法框架 ·基本思路 查找f可增路P -反复查找是否存在f可增路P ·如果存在,沿P则更新当前流f P=null? ·否则f即为最大流 N FORD-FULKERSON(G.S.t) for each edge (u.v)EG.E 更新当前流f 2 (4,v)f=0 while there exists a path p from s to t in the residual network Gf 4 cf(p)=mincf(u.v):(u.v)is in p 5 for each edge (u.v)in p 返回当前流f if(u,v)∈E 7 (u.v).f=(u.v).f+cf(p) else (v.u).f=(v.u).f-cf(p)
Ford-Fulkerson算法框架 • 基本思路 – 反复查找是否存在𝒇可增路P • 如果存在,沿P则更新当前流𝒇 • 否则𝒇即为最大流 查找𝒇可增路P P=null? 更新当前流𝒇 返回当前流𝒇 N Y

Ford-Fulkerson标号算法 ·给定网络G(W,E),求G的一个最大流 0.初始化:a∈E,令f(a)=0;∥初始流量为0 l(v)实际表示的是S 1.l(s)=o;L={s;S=0/L表示已标未查集,S表示已标已查集 经过当前所查找的 一条路P到达v可能 2.while(L≠o) 的最大流量cr(P) 从L中任意取一个节点u,对所有v∈N()-(LUS): 处理正向弧 如果a=(u,v)∈E且c(a)>f(a),则给v标号: (u,+,l() l(v)=minfl(u),c(a)-f(a);L=L+v} 处理反向弧 如果a=(v,))∈E且f(a)>0,则给v标号: (u,-,l(v) l(v)=minfl(u),f(a),L=L+v 更新f: -L=L-{u};S=S+{uu处理完毕 1.令z=y ift∈L,则存在f可增路,break 2.如果z的标号为(w,+,l(2) 3.ift∈L(存在f可增路) 令f(w,z)=f(w,z)+ly) ·顺延标号更新流f 如果z的标号为(w,-,l(z),令 ·转第1步 f((z,w))=f((z,w))-L(y); 4.fL=0不存在f可增路:流f为最大流且(S,⊙为最小割,返回f 3.如果w≠x,令z=w并转2;
Ford-Fulkerson标号算法 • 给定网络𝐺(𝑉, 𝐸) ,求G的一个最大流 • 0.初始化: ∀𝑎 ∈ 𝐸,令𝑓 𝑎 = 0;//初始流量为0 • 1. 𝑙 𝑠 = ∞; 𝐿 = 𝑠 ; 𝑆 = ∅//L表示已标未查集,S表示已标已查集 • 2.while(𝐿 ≠ ∅) – 从𝐿中任意取一个节点𝑢, 对所有𝑣 ∈ 𝑁 𝑢 − (𝐿 ∪ 𝑆): • 如果𝑎 = 𝑢, 𝑣 ∈ 𝐸且𝑐 𝑎 > 𝑓(𝑎),则给𝑣标号: 𝑙 𝑣 = min 𝑙 𝑢 , 𝑐 𝑎 − 𝑓 𝑎 ; 𝐿 = 𝐿 + {𝑣} • 如果𝑎 = 𝑣, 𝑢 ∈ 𝐸且𝑓 𝑎 > 0,则给𝑣标号: 𝑙 𝑣 = min 𝑙 𝑢 ,𝑓 𝑎 , 𝐿 = 𝐿 + {𝑣} – 𝐿 = 𝐿 − 𝑢 ; 𝑆 = 𝑆 + {𝑢}//u处理完毕 – if𝑡 ∈ 𝐿,则存在𝑓可增路, break • 3. if𝑡 ∈ 𝐿(存在𝑓可增路) • 顺延标号更新流𝑓 • 转第1步 • 4.if L=∅不存在𝒇可增路;流𝑓为最大流且 𝑆, 𝑆ҧ为最小割, 返回𝑓 (𝑢, +, 𝑙(𝑣)) (𝑢, −, 𝑙(𝑣)) 更新f: 1. 令z=y 2. 如果z的标号为 𝑤, +, 𝑙 𝑧 , 令𝑓 𝑤, 𝑧 = 𝑓 𝑤, 𝑧 + 𝑙(𝑦); 如果z的标号为 𝑤, −, 𝑙 𝑧 ,令 𝑓 𝑧, 𝑤 = 𝑓 𝑧,𝑤 − 𝑙(𝑦); 3. 如果𝑤 ≠ 𝑥,令𝑧 = 𝑤并转2; 𝑙 𝑣 实际表示的是s 经过当前所查找的 一条路P到达v可能 的最大流量𝑐𝑓 𝑃 处理正向弧 处理反向弧
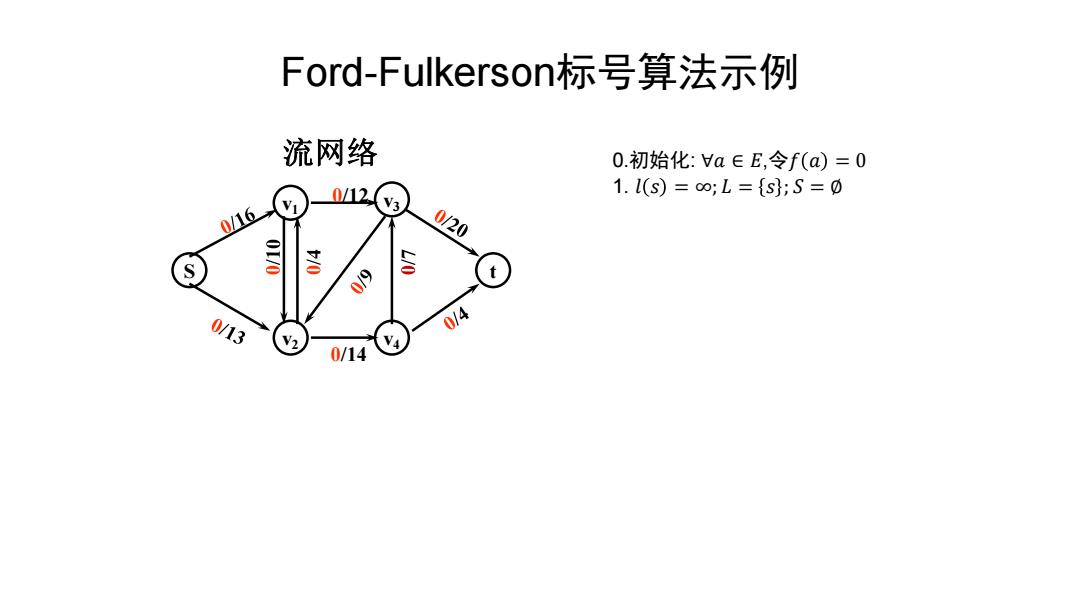
Ford-Fulkerson标号算法示例 流网络 0.初始化:a∈E,令f(a)=0 0/L12 1.l(S)=o;L={S;S=0 0/16 0/20 00 019 S 0/13 0/4 V2 0/14 V4
S t v1 v2 v3 v4 0/12 0/14 流网络 Ford-Fulkerson标号算法示例 0.初始化: ∀𝑎 ∈ 𝐸,令𝑓 𝑎 = 0 1. 𝑙 𝑠 = ∞; 𝐿 = 𝑠 ; 𝑆 = ∅
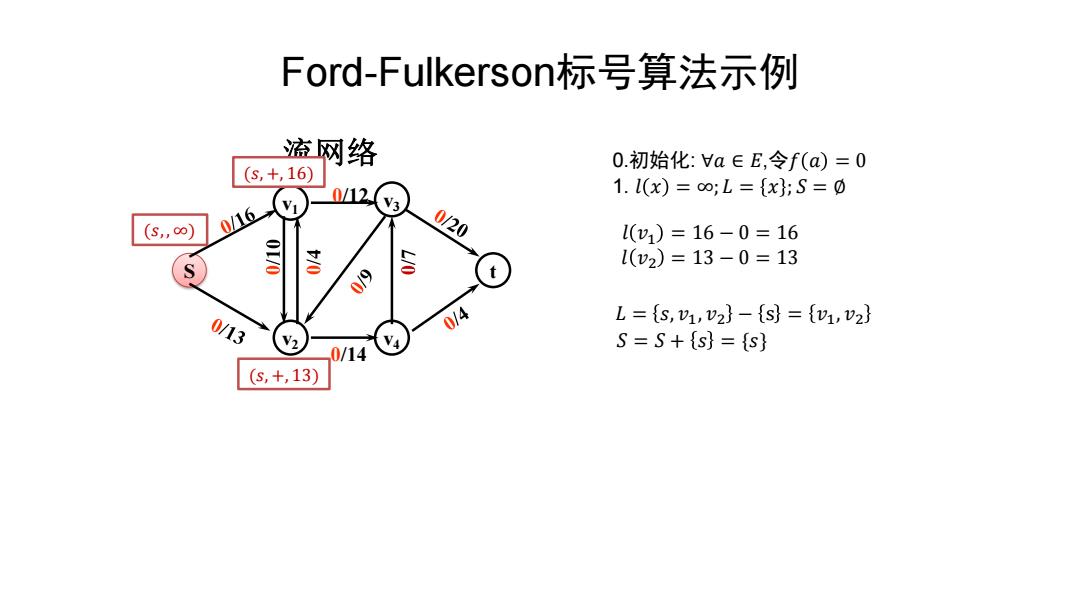
Ford-Fulkerson标号算法示例 流网络 0.初始化:Ha∈E,令f(a)=0 (s,+,16 0/12 1.l(x)=o;L={x};S=0 (S,∞) 0/16 0/20 1(v1)=16-0=16 070 l(v2)=13-0=13 09 S 0/13 0/4 L={s,1,v2}-{S={1,v2} V2 S=S+{s}={S} 0/14 V4 (s,+,13)
S t v1 v2 v3 v4 0/12 0/14 流网络 Ford-Fulkerson标号算法示例 0.初始化: ∀𝑎 ∈ 𝐸,令𝑓 𝑎 = 0 1. 𝑙 𝑥 = ∞; 𝐿 = 𝑥 ; 𝑆 = ∅ 𝑙 𝑣1 = 16 − 0 = 16 𝑙 𝑣2 = 13 − 0 = 13 (𝑠, +, 16) (𝑠, +, 13) (𝑠, , ∞) 𝐿 = 𝑠, 𝑣1, 𝑣2 − s = 𝑣1, 𝑣2 𝑆 = 𝑆 + 𝑠 = {𝑠}

Ford-Fulkerson标号算法示例 流网络 L={v1,v2} (s,+,16 S={s} 0/12 (S,0∞) 0/16 0/20 00 S l(v3)=min(13,0)=0,不标记 019 l(v4)=min(13,14-0)=13,标记 0/13 0/4 L={1v2}+{v4}-{v2}={v1v4} V2 0/14 V4 S=S+{v2}={s,v2} (s,+,13) (v2,+,13)
S t v1 v2 v3 v4 0/12 0/14 流网络 Ford-Fulkerson标号算法示例 𝑙 𝑣3 = min(13,0) = 0 ,不标记 𝑙 𝑣4 = min(13,14 − 0) =13 ,标记 (𝑠, +, 16) (𝑠, +, 13) (𝑠, , ∞) 𝐿 = 𝑣1, 𝑣2 𝑆 = {𝑠} (𝑣2, +, 13) 𝐿 = 𝑣1, 𝑣2 + {𝑣4} − 𝑣2 = 𝑣1, 𝑣4 𝑆 = 𝑆 + 𝑣2 = {𝑠, 𝑣2}
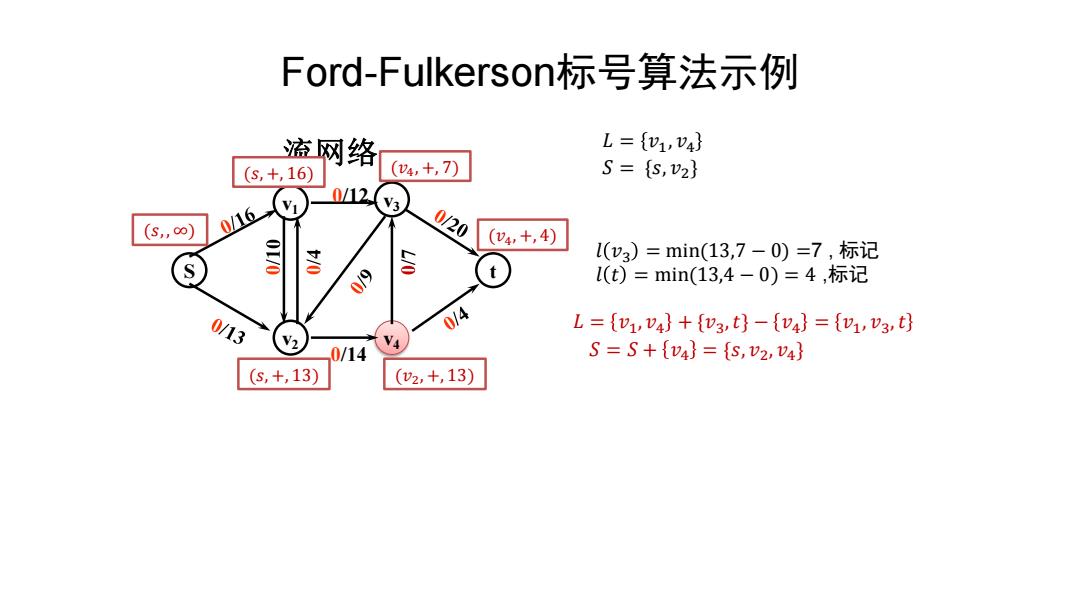
Ford-Fulkerson标号算法示例 流网络 L={v1,v4} (S,+,16 (4,+,7) S={S,v2} 0/12. /16 V3 (S,0∞) 0/20 (v4,+,4) 00 S l(v3)=min(13,7-0)=7,标记 l(t)=min(13,4-0)=4,标记 0/13 0/4 L={v1,v4}+{v3,t}-{v4}={v1,v3,t} V2 0/14 S=S+{v4}={S,v2,v4} (s,+,13) (v2,+,13)
S t v1 v2 v3 v4 0/12 0/14 流网络 Ford-Fulkerson标号算法示例 𝑙 𝑣3 = min(13,7 − 0) =7 , 标记 𝑙 𝑡 = min(13,4 − 0) = 4 ,标记 (𝑠, +, 16) (𝑠, +, 13) (𝑠, , ∞) 𝐿 = 𝑣1, 𝑣4 𝑆 = {𝑠, 𝑣2} (𝑣2, +, 13) 𝐿 = 𝑣1, 𝑣4 + {𝑣3,𝑡} − 𝑣4 = 𝑣1, 𝑣3,𝑡 𝑆 = 𝑆 + 𝑣4 = {𝑠, 𝑣2, 𝑣4} (𝑣4, +, 7) (𝑣4, +, 4)
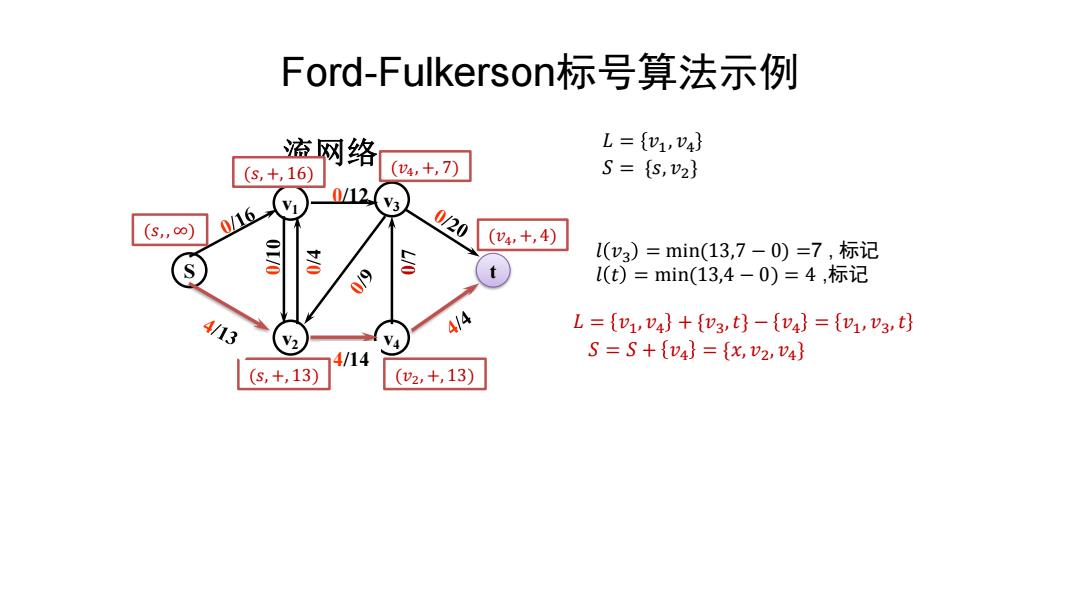
Ford-Fulkerson标号算法示例 流网络 L={v1,v4} (S,+,16 (4,+,7) S={S,v2} 012. 116 V3 (S,0∞) 0/20 (U4,+,4) 00 S l(v3)=min(13,7-0)=7,标记 t l(t)=min(13,4-0)=4,标记 4/13 414 L={v1,v4}+{v3,t}-{v4}={v1,v3,t} V2 4/14 S=S+{v4}={x,2,v4} (s,+,13) (v2,+,13)
S t v1 v2 v3 v4 0/12 0/14 流网络 Ford-Fulkerson标号算法示例 𝑙 𝑣3 = min(13,7 − 0) =7 , 标记 𝑙 𝑡 = min(13,4 − 0) = 4 ,标记 (𝑠, +, 16) (𝑠, , ∞) 𝐿 = 𝑣1, 𝑣4 𝑆 = {𝑠, 𝑣2} (𝑣2, +, 13) 𝐿 = 𝑣1, 𝑣4 + {𝑣3,𝑡} − 𝑣4 = 𝑣1, 𝑣3,𝑡 𝑆 = 𝑆 + 𝑣4 = {𝑥, 𝑣2, 𝑣4} (𝑣4, +, 7) (𝑣4, +, 4) 4/14 (𝑠, +, 13)
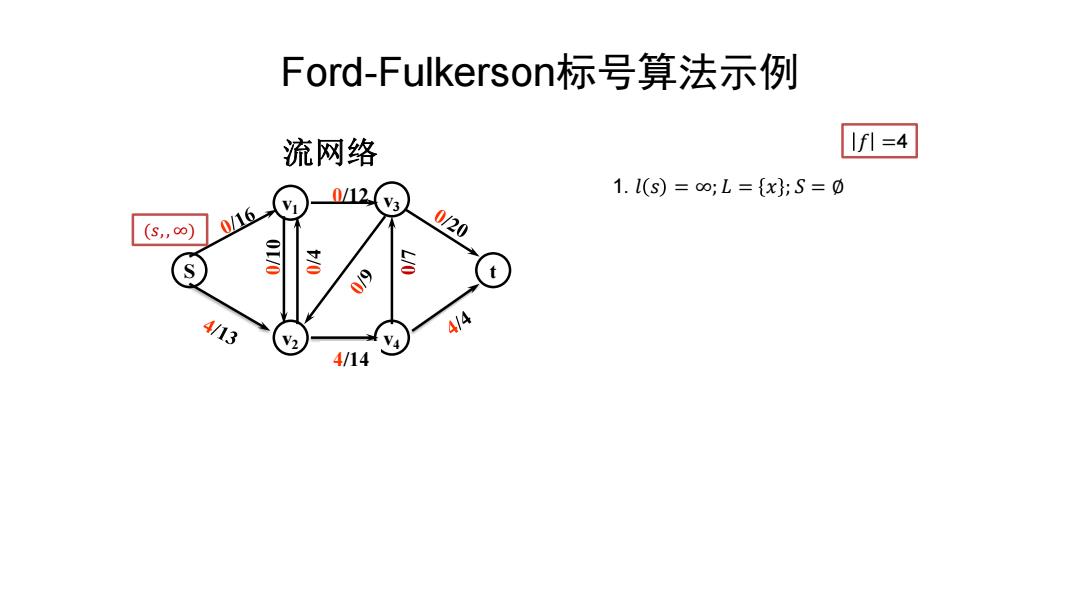
Ford-Fulkerson标号算法示例 流网络 1f升=4 0/L12 1.l(S=o;L={x};S=0 (S,∞) 0/16 0/20 00 8 S 4/13 4/4 4/14
S t v1 v2 v3 v4 0/12 0/14 流网络 Ford-Fulkerson标号算法示例 (𝑠, , ∞) 4/14 1. 𝑙 𝑠 = ∞; 𝐿 = 𝑥 ; 𝑆 = ∅ 𝑓 =4