
计算机问题求解一论题3-14 线性规划 2020年12月29日
计算机问题求解 – 论题3-14 - 线性规划 2020年12月29日
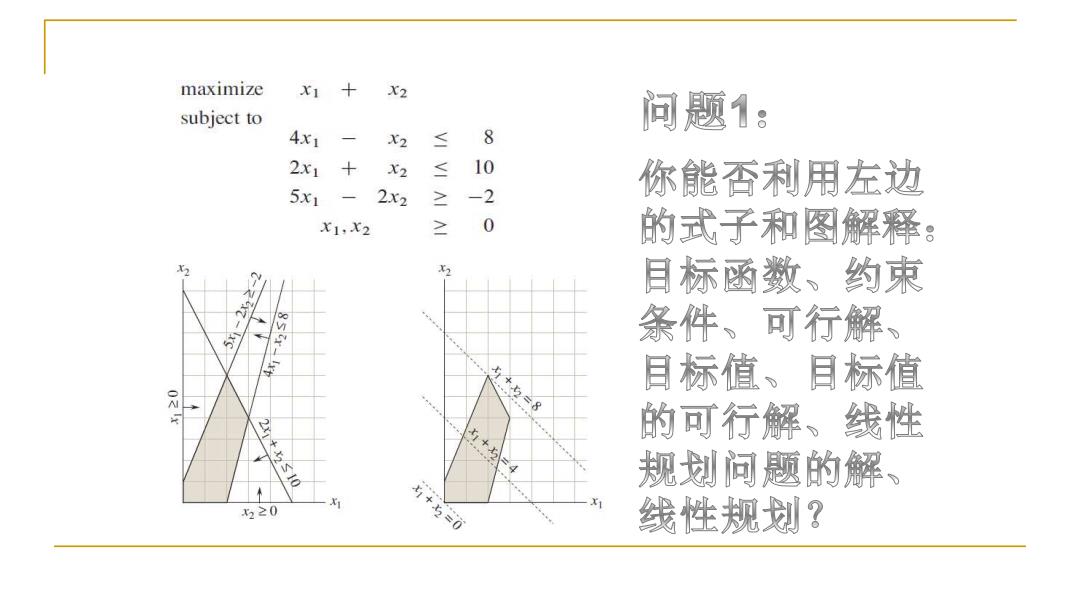
maximize X1 X2 subject to 问题1: 4x1 X2 ≤ 8 2x1 X2 ≤ 10 5x1 你能否利用左边 2x2 ≥ -2 X1,X2 ≥ 0 的式子和图解释: 222-2 目标函数、约束 条件、可行解、 =8 目标值、目标值 21+x10 x+x 的可行解、线性 规划问题的解、 5≥0 +=0 线性规划?
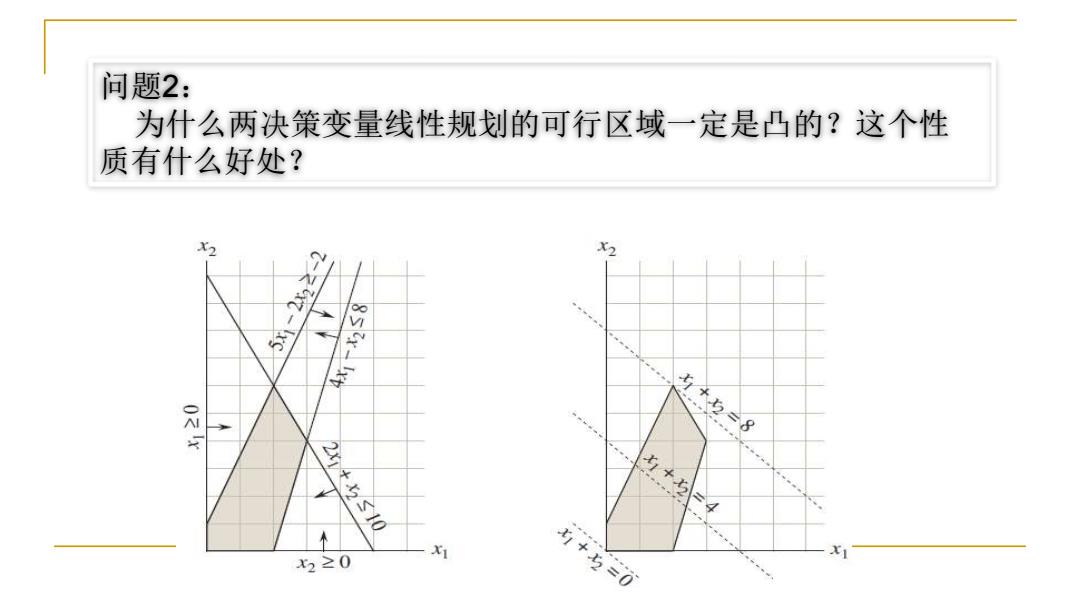
问题2: 为什么两决策变量线性规划的可行区域一定是凸的?这个性 质有什么好处? X2 X2 5x-2x22-2 2x4x2S10 x1+ 4 个 x2≥0 X1 +三0
问题2: 为什么两决策变量线性规划的可行区域一定是凸的?这个性 质有什么好处?
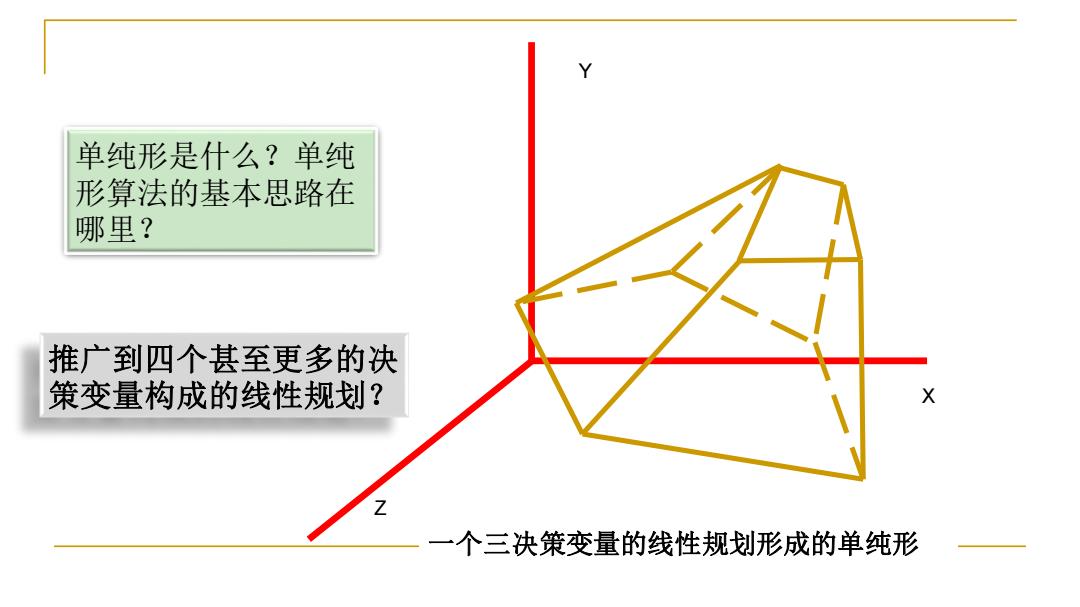
单纯形是什么?单纯 形算法的基本思路在 哪里? 推广到四个甚至更多的决 策变量构成的线性规划? Z 一个三决策变量的线性规划形成的单纯形
一个三决策变量的线性规划形成的单纯形 Y X Z 单纯形是什么?单纯 形算法的基本思路在 哪里? 推广到四个甚至更多的决 策变量构成的线性规划?

问题3: 线性规划问题中的不等 式能不能用严格的大于 或小于?

线性规划问题的标准形式 maximize j=1 subject to ax≤bi for i=1,2,,m j=1 x≥0forj=1,2,..,n maximize cTx subject to Ax ≤b x≥0
线性规划问题的标准形式

mizing a linear function subject to linear constraints,into standard form.A linear program might not be in standard form for any of four possible reasons: 1.The objective function might be a minimization rather than a maximization. 2.There might be variables without nonnegativity constraints. 3.There might be equality constraints,which have an equal sign rather than a less-than-or-equal-to sign. 4.There might be ineguality constraints,but instead of having a less-than-or- equal-to sign,they have a greater-than-or-equal-to sign

minimize -2x1+3x2 subject to x1+ X2 =7 X1- 2x2 4 X1 ≥0 问题4: 为什么说这不是“标准形式”? 如何将它”转化”为标准形式?

minimize -2x1+3x2 maximize 2x1 3x2 subject to subject to x1+ X2 =7 x1+ X2 =7 x1- 2x2 ≤ 4 x1-2x2 4 xI 0. X1 ≥0 maximize 2x1-3x2+3x2 subject to x1+ x =7 ←☐令X2=X2'-X2 x1-2x 2x2 ≤4 x1.x2.x2 0. 很“无厘 头”?
令x2=x2 ’-x2 ” 很“无厘 头”?

maximize 2x1-3x2+3x subject to x1+3 x2 =7 x1-2x2 2x2 ≤4 X1:X2.X2 0. maximize 2x1 -3x2+3x subject to x1+x2 -x2 ≤7 X1+x2 x ≥7 x1-2x2 2x2 ≤ 4 X1.x2.x2 0 maximize CTX maximize 2x1-3x2+3x3 subject to x1+x2 3≤ > subject to -x1-x2 X3 ≤-7 Ax≤ b 2x1-2x2 +2x3 4 0. x≥ 0. X1,X2,X3